15.1 轴对称图形第2课时轴对称课件(共20张PPT)2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 15.1 轴对称图形第2课时轴对称课件(共20张PPT)2024-2025学年度八年级上册沪科版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 580.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-04 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
沪科版
15.1.2 轴对称
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
学习目标
1.了解两个图形关于某直线对称的概念.
2.了解轴对称图形与两个图形关于某直线对称的区别和联系.
3.能识别简单的轴对称现象及其对称轴(直线),能找出两个图形关于某直线对称的对称点.
重点
难点
新课引入
问题1:什么是轴对称图形?请画出一个轴对称图形,并找出它的对称轴.
如果一个平面图形沿着一条直线折叠,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做它的对称轴.
问题2:在一张半透明的纸的左边画一只左脚印,再把这张纸对折后描图,打开对折的纸,就能得到相应的右脚印,那么此时左脚印和右脚印有什么关系?
l
左脚印和右脚印关于折痕l对称.
那么此时左脚印和右脚印能不能叫做轴对称图形?为什么?
不能,因为轴对称图形是一个图形具有的特点
那么像这种两个图形的对称我们应该怎么理解呢?这就是本节课所要学习的内容.
新知学习
A′
A
B
C
B′
C′
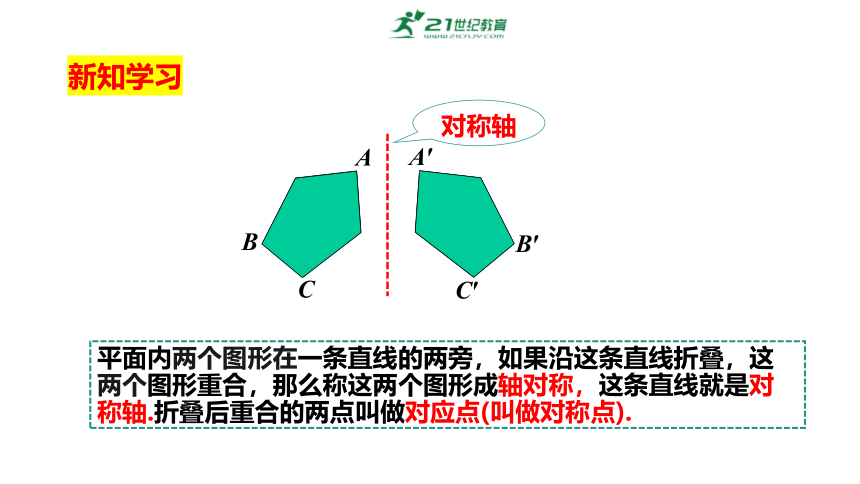
对称轴
平面内两个图形在一条直线的两旁,如果沿这条直线折叠,这两个图形重合,那么称这两个图形成轴对称,这条直线就是对称轴.折叠后重合的两点叫做对应点(叫做对称点).
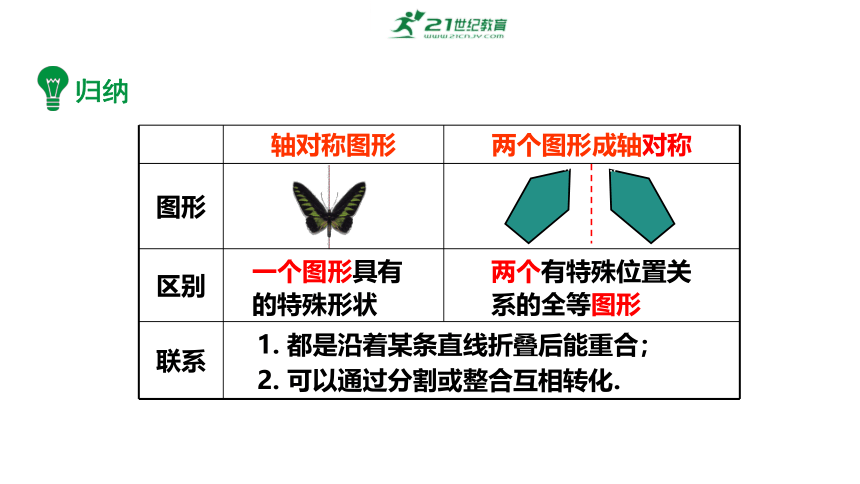
归纳
轴对称图形 两个图形成轴对称
图形
区别
联系 两个有特殊位置关系的全等图形
1. 都是沿着某条直线折叠后能重合;
2. 可以通过分割或整合互相转化.
一个图形具有的特殊形状
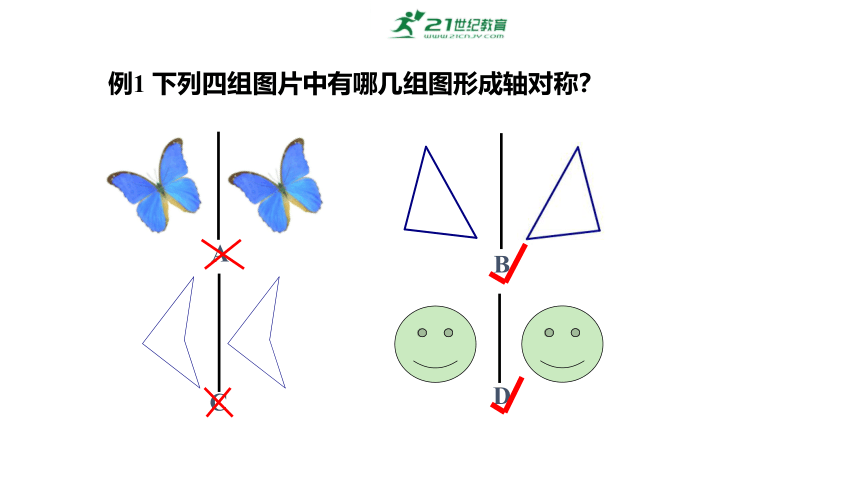
例1 下列四组图片中有哪几组图形成轴对称?
B
D
C
A
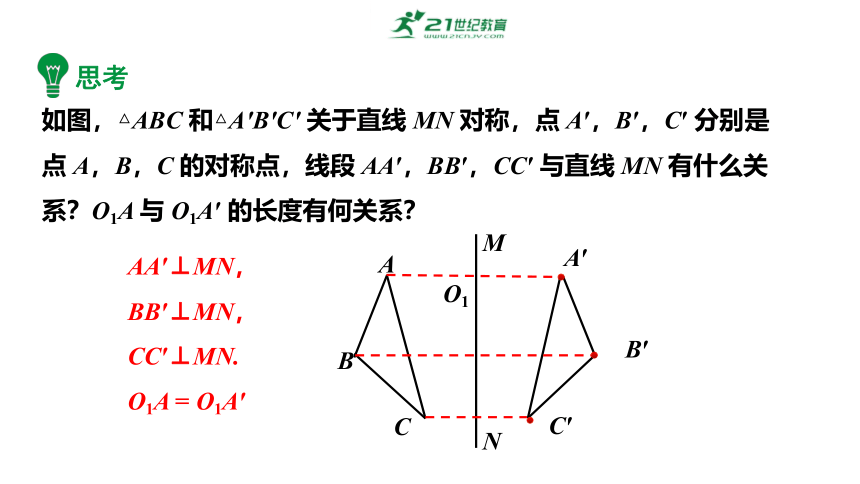
如图,△ABC 和△A′B′C′ 关于直线 MN 对称,点 A′,B′,C′ 分别是点 A,B,C 的对称点,线段 AA′,BB′,CC′ 与直线 MN 有什么关系?O1A 与 O1A′ 的长度有何关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
O1A = O1A′
O1
思考
如图,MN⊥AA′, AP = A′P.
直线 MN 是线段 AA′ 的垂直平分线.
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,又叫做线段的中垂线.
图形轴对称的性质
反过来,成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
如图,MN 垂直平分 AA ′,MN 垂直平分 BB ′.
A
B
A′
B′
M
N
A.130° B.150°
C.40° D.65°
解析:因为这种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,
所以∠BAC=∠DAC=75°,∠BCA=∠DCA.
所以∠BCA=180°-75°-40°=65°. 所以∠BCD=130°.
A
例2 如图,一种滑翔伞的形状是左右成轴对称的四边形 ABCD,其中∠BAD = 150°,∠B = 40°,则∠BCD 的度数是 ( )
探究
问题1:如何画一个点关于某条直线的轴对称图形?
画出点 A 关于直线 l 的对称点 A′.
﹒
l
A
﹒
A′
O
作法:
(1) 过点 A 作 l 的垂线,垂足为点 O;
(2) 在垂线上 l 的另一侧截取 OA′ = OA.
则点 A′ 就是点 A 关于直线 l 的对称点.
问题2:如何画一条线段的对称图形?
已知线段 AB,画出 AB 关于直线 l 的对称线段.
A
B
(图1)
(图2)
(图3)
A
B
l
l
A
B
l
A′
A′
A′
B′
(B′)
B′
问题3:如果有一个图形(如三角形、四边形)和一条直线,如何画出这个图形关于这条直线对称的图形呢?
如图,已知△ABC 和直线 l,作出与△ABC关于直线 l 对称的图形.
作法:(1) 过点 A 画直线 l 的垂线,垂足为点 O,在垂线上截取 OA′ = OA,A′ 就是点 A 关于直线 l 的对称点.
(3) 连接 A′B′,B′C′,C′A′,得到的△A′B′C′ 即为所求.
(2) 同理,分别画出点 B,C 关于直线 l 的对称点 B′,C′.
A
B
C
A′
B′
C′
O
画轴对称图形的方法:
(1)找特征点
(2)作垂线
(3)截取等长
(4)依次连线
例3 在 3×3 的正方形格点图中,有格点△ABC 和△DEF,且△ABC 和△DEF 关于某直线成轴对称,请在下面给出的图中画出 4 个这样的△DEF.
A
B
C
A
B
C
A
B
C
A
B
C
(F)
(D)
E
(E)
F
D
(F)
D
E
(D)
(E)
F
随堂练习
1. 如图,△ABC 与△DEF 关于直线 MN 轴对称,则以下结论中错误的是( )
A.AB∥DF
B.∠B = ∠E
C.AB = DE
D.AD 的连线被 MN 垂直平分
A
A
B
C
D
E
F
N
M
B
A
C
B′
D
E
C′
(A′)
2.画一画:
(1)任意画△ABC,过A点任意画一条直线l ;
(2)作△ A'B'C'与△ABC关于直线l对称.
4. 如图,Rt△ABC 中,∠ACB = 90°,∠A = 50°,将其折叠,使点 A 落在边 CB 上 A′ 处,折痕为 CD,则∠A′DB 的度数为______.
10°
A
D
C
A′
B
课堂小结
轴对称
两个图形
成轴对称
定义:平面内两个图形在一条直线的两旁,如果沿这条直线折叠,这两个图形重合,那么称这两个图形成轴对称,这条直线就是对称轴.折叠后重合的两点叫做对应点(又叫做对称点).
性质:对称轴是任何一对对应点所连线段的垂直平分线.
方法:(1)找特征点(2)作垂线(3)截取等长
(4)依次连线
画轴对称图形
原理:轴对称变化不改变图形的形状和大小
沪科版
15.1.2 轴对称
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
学习目标
1.了解两个图形关于某直线对称的概念.
2.了解轴对称图形与两个图形关于某直线对称的区别和联系.
3.能识别简单的轴对称现象及其对称轴(直线),能找出两个图形关于某直线对称的对称点.
重点
难点
新课引入
问题1:什么是轴对称图形?请画出一个轴对称图形,并找出它的对称轴.
如果一个平面图形沿着一条直线折叠,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做它的对称轴.
问题2:在一张半透明的纸的左边画一只左脚印,再把这张纸对折后描图,打开对折的纸,就能得到相应的右脚印,那么此时左脚印和右脚印有什么关系?
l
左脚印和右脚印关于折痕l对称.
那么此时左脚印和右脚印能不能叫做轴对称图形?为什么?
不能,因为轴对称图形是一个图形具有的特点
那么像这种两个图形的对称我们应该怎么理解呢?这就是本节课所要学习的内容.
新知学习
A′
A
B
C
B′
C′
对称轴
平面内两个图形在一条直线的两旁,如果沿这条直线折叠,这两个图形重合,那么称这两个图形成轴对称,这条直线就是对称轴.折叠后重合的两点叫做对应点(叫做对称点).
归纳
轴对称图形 两个图形成轴对称
图形
区别
联系 两个有特殊位置关系的全等图形
1. 都是沿着某条直线折叠后能重合;
2. 可以通过分割或整合互相转化.
一个图形具有的特殊形状
例1 下列四组图片中有哪几组图形成轴对称?
B
D
C
A
如图,△ABC 和△A′B′C′ 关于直线 MN 对称,点 A′,B′,C′ 分别是点 A,B,C 的对称点,线段 AA′,BB′,CC′ 与直线 MN 有什么关系?O1A 与 O1A′ 的长度有何关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
O1A = O1A′
O1
思考
如图,MN⊥AA′, AP = A′P.
直线 MN 是线段 AA′ 的垂直平分线.
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,又叫做线段的中垂线.
图形轴对称的性质
反过来,成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
如图,MN 垂直平分 AA ′,MN 垂直平分 BB ′.
A
B
A′
B′
M
N
A.130° B.150°
C.40° D.65°
解析:因为这种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,
所以∠BAC=∠DAC=75°,∠BCA=∠DCA.
所以∠BCA=180°-75°-40°=65°. 所以∠BCD=130°.
A
例2 如图,一种滑翔伞的形状是左右成轴对称的四边形 ABCD,其中∠BAD = 150°,∠B = 40°,则∠BCD 的度数是 ( )
探究
问题1:如何画一个点关于某条直线的轴对称图形?
画出点 A 关于直线 l 的对称点 A′.
﹒
l
A
﹒
A′
O
作法:
(1) 过点 A 作 l 的垂线,垂足为点 O;
(2) 在垂线上 l 的另一侧截取 OA′ = OA.
则点 A′ 就是点 A 关于直线 l 的对称点.
问题2:如何画一条线段的对称图形?
已知线段 AB,画出 AB 关于直线 l 的对称线段.
A
B
(图1)
(图2)
(图3)
A
B
l
l
A
B
l
A′
A′
A′
B′
(B′)
B′
问题3:如果有一个图形(如三角形、四边形)和一条直线,如何画出这个图形关于这条直线对称的图形呢?
如图,已知△ABC 和直线 l,作出与△ABC关于直线 l 对称的图形.
作法:(1) 过点 A 画直线 l 的垂线,垂足为点 O,在垂线上截取 OA′ = OA,A′ 就是点 A 关于直线 l 的对称点.
(3) 连接 A′B′,B′C′,C′A′,得到的△A′B′C′ 即为所求.
(2) 同理,分别画出点 B,C 关于直线 l 的对称点 B′,C′.
A
B
C
A′
B′
C′
O
画轴对称图形的方法:
(1)找特征点
(2)作垂线
(3)截取等长
(4)依次连线
例3 在 3×3 的正方形格点图中,有格点△ABC 和△DEF,且△ABC 和△DEF 关于某直线成轴对称,请在下面给出的图中画出 4 个这样的△DEF.
A
B
C
A
B
C
A
B
C
A
B
C
(F)
(D)
E
(E)
F
D
(F)
D
E
(D)
(E)
F
随堂练习
1. 如图,△ABC 与△DEF 关于直线 MN 轴对称,则以下结论中错误的是( )
A.AB∥DF
B.∠B = ∠E
C.AB = DE
D.AD 的连线被 MN 垂直平分
A
A
B
C
D
E
F
N
M
B
A
C
B′
D
E
C′
(A′)
2.画一画:
(1)任意画△ABC,过A点任意画一条直线l ;
(2)作△ A'B'C'与△ABC关于直线l对称.
4. 如图,Rt△ABC 中,∠ACB = 90°,∠A = 50°,将其折叠,使点 A 落在边 CB 上 A′ 处,折痕为 CD,则∠A′DB 的度数为______.
10°
A
D
C
A′
B
课堂小结
轴对称
两个图形
成轴对称
定义:平面内两个图形在一条直线的两旁,如果沿这条直线折叠,这两个图形重合,那么称这两个图形成轴对称,这条直线就是对称轴.折叠后重合的两点叫做对应点(又叫做对称点).
性质:对称轴是任何一对对应点所连线段的垂直平分线.
方法:(1)找特征点(2)作垂线(3)截取等长
(4)依次连线
画轴对称图形
原理:轴对称变化不改变图形的形状和大小
