15.1轴对称图形第3课时平面直角坐标系中的轴对称课件(共20张PPT)2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 15.1轴对称图形第3课时平面直角坐标系中的轴对称课件(共20张PPT)2024-2025学年度八年级上册沪科版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 916.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-04 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
沪科版
15.1.3 平面直角坐标
系中的轴对称
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.探究在平面直角坐标系中关于x轴和y轴对称点的坐标特点.
2.能在平面直角坐标系中画出一些简单的关于x轴和y轴的对称图形.
3.能运用坐标系中的轴对称特点解决简单的问题.
学习目标
重点
难点
(1)什么是轴对称?
根据上节课所学,回答下列问题
平面内两个图形在一条直线的两旁,如果沿着这条直线折叠,这两个图形能够重合,那么称这两个图形成轴对称,这条直线就是对称轴.折叠后重合的两点叫做对应点
(2)什么是垂直平分线?
经过线段的中点并且垂直于这条线段的直线叫做这条线段的垂直平分线
新课引入
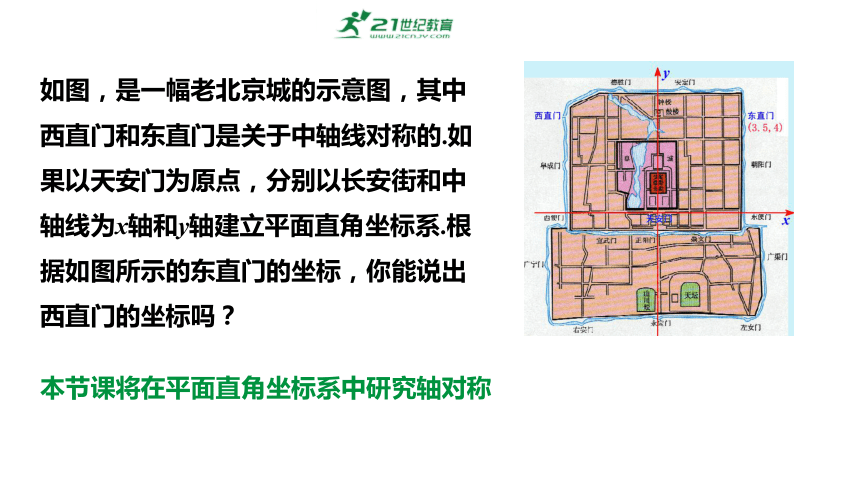
如图,是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系.根据如图所示的东直门的坐标,你能说出西直门的坐标吗?
本节课将在平面直角坐标系中研究轴对称
在平面直角坐标系中,如何作出图形的轴对称图呢 下面只介绍以特殊直线(坐标轴)为对称轴的情形.
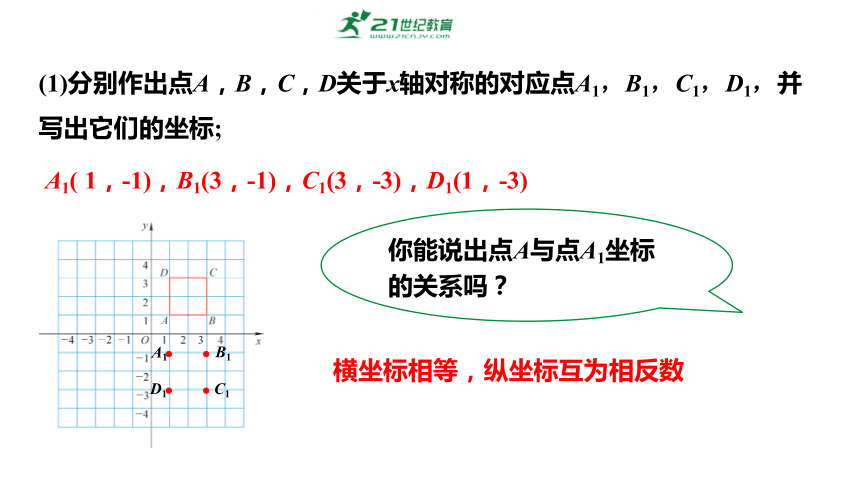
如图,在平面直角坐标系中,正方形ABCD四个顶点
的坐标分别为A( 1 ,1),B(3,1),C(3,3),D(1,3).
思考
新知学习
(1)分别作出点A,B,C,D关于x轴对称的对应点A1,B1,C1,D1,并写出它们的坐标;
A1
B1
C1
D1
A1( 1,-1),B1(3,-1),C1(3,-3),D1(1,-3)
你能说出点A与点A1坐标的关系吗?
横坐标相等,纵坐标互为相反数
已知点的坐标 A(l, 1) B(3, 1) C(3, 3) D(1,3)
关于x轴对称的点的坐标 A1(__,__ ) B1(__,__ ) C1(__,__ ) D1(__,__ )
1 -1
3 -1
3 -3
1 -3
总结:点(x,y)关于x轴对称的点的坐标为(x,-y),即横坐标不变,纵坐标互为相反数.
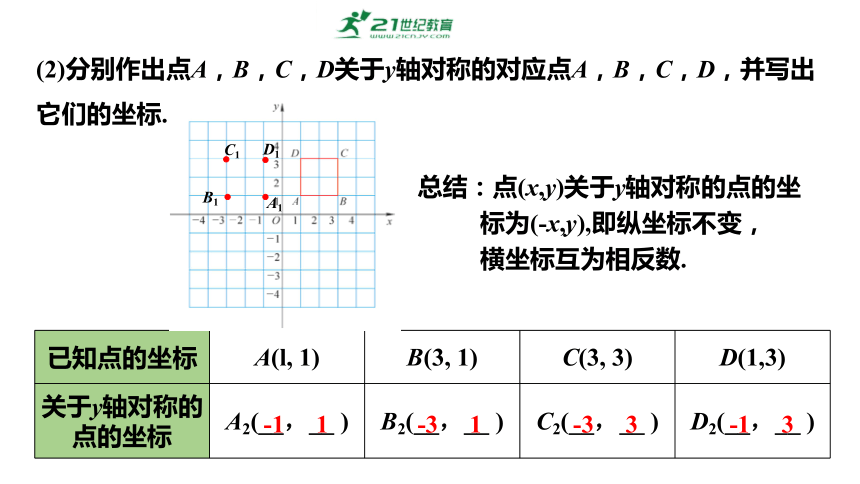
(2)分别作出点A,B,C,D关于y轴对称的对应点A,B,C,D,并写出它们的坐标.
已知点的坐标 A(l, 1) B(3, 1) C(3, 3) D(1,3)
关于y轴对称的点的坐标 A2(__,__ ) B2(__,__ ) C2(__,__ ) D2(__,__ )
-1 1
-3 1
-3 3
-1 3
A1
B1
C1
D1
总结:点(x,y)关于y轴对称的点的坐
标为(-x,y),即纵坐标不变,
横坐标互为相反数.
在平面直角坐标系中,
已知点P(x,y),它关于x轴对称的点的坐标为P1(___,___)
它关于y轴对称的点的坐标为P2(___,___).
x -y
-x y
归纳
如图,是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系.根据如图所示的东直门的坐标,现在你能说出西直门的坐标吗?
西直门(-3.5,4)
例1 如图,梯形ABCD关于y轴对称,点A的坐标为(-3,3),点B的坐标为(-2,0),写出点C和点D的坐标,并求出梯形ABCD的面积
解:点D与点A(-3,3)关于y轴对称.
∴点D的坐标为(3.3).
同理点C的坐标为(2,0).
∴AD=|3-(-3)|=6,BC=|2-(-2)|=4.
∴S梯形=
例2 已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点A、B关于x轴对称,求a、b的值;
(2)若A、B关于y轴对称,求(4a+b)2018的值.
解:(1)∵点A、B关于x轴对称,
∴2a-b=2b-1,5+a-a+b=0,
解得a=-8,b=-5;
(2)∵A、B关于y轴对称,
∴2a-b+2b-1=0,5+a=-a+b,
解得a=-1,b=3,
∴(4a+b)2018=1.
例3 平面直角坐标系中,△ABC 的三个顶点坐标分别为 A(0,4),B(2,4),C(3,-1).
(1)试在平面直角坐标系中,标出 A、B、C 三点;
x
y
O
A(0,4)
B(2,4)
C (3,-1)
(2)若△ABC 与△A'B'C' 关于 x 轴对称,画出△A'B'C',并写出 A'、B'、C' 的坐标.
x
y
O
A(0,4)
B(2,4)
C (3,-1)
A' (0,-4)
B'(2,-4)
C'(3,1)
对于这类问题,只要先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
在坐标系中作已知图形的对称图形
(一找二描三连)
分析:由关于y轴对称的点的坐标特征得m+2=5,
n+6=3,解得,m=3,n=-3.
1. 已知点A(m+2,3),B(-5,n+6)关于y轴对称,则m=________,
n=________.
3
-3
随堂练习
2.平面直角坐标系内的点A(-1,2)与点B(-1,-2)关于( )
A.y轴对称 B.x轴对称
C.原点对称 D.直线y=x对称
3.在平面直角坐标系中,将点A(-1,2)向右平移3个单位长度得到点
B,则点B关于x轴的对称点C的坐标是( )
A.(-4,-2) B.(2,2)
C.(-2,2) D.(2,-2)
D
B
4.如图,在平面直角坐标系中,点P(-1,2)关于直线x=1的对称点的坐标为( )
A.(1,2)
B.(2,2)
C.(3,2)
D.(4,2)
C
5.已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),
C(-1,3),作出△ABC关于y轴对称的图形.
解:点A(-3,5),B(-4,1),C(-1,3),
关于y轴的对称点分别为
A′(3,5),B′(4,1),C′(1,3).
依次连接A′B′,B′C′,C′A′,
就得到△ABC关于y轴对称的
△A′B′C′.
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
A
C
B
B ′
A′
C ′
x
y
在坐标系中
作关于坐标
轴对称的图形
点(x,y)关于x轴对称的点的坐标为(x,-y),即
横坐标相等,纵坐标互为相反数;
点(x,y)关于y轴对称的点的坐标为(-x,y),即
横坐标互为相反数,纵坐标相等.
先求出已知图形中的一些特殊点(如多边形的顶点)
的对应点的坐标,描出并连接这些点,就可以得到这
个图形的轴对称图形.(一找二描三连)
平面直角
坐标系中
的轴对称
关于坐标轴
对称的点的
坐标特征
课堂小结
沪科版
15.1.3 平面直角坐标
系中的轴对称
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.探究在平面直角坐标系中关于x轴和y轴对称点的坐标特点.
2.能在平面直角坐标系中画出一些简单的关于x轴和y轴的对称图形.
3.能运用坐标系中的轴对称特点解决简单的问题.
学习目标
重点
难点
(1)什么是轴对称?
根据上节课所学,回答下列问题
平面内两个图形在一条直线的两旁,如果沿着这条直线折叠,这两个图形能够重合,那么称这两个图形成轴对称,这条直线就是对称轴.折叠后重合的两点叫做对应点
(2)什么是垂直平分线?
经过线段的中点并且垂直于这条线段的直线叫做这条线段的垂直平分线
新课引入
如图,是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系.根据如图所示的东直门的坐标,你能说出西直门的坐标吗?
本节课将在平面直角坐标系中研究轴对称
在平面直角坐标系中,如何作出图形的轴对称图呢 下面只介绍以特殊直线(坐标轴)为对称轴的情形.
如图,在平面直角坐标系中,正方形ABCD四个顶点
的坐标分别为A( 1 ,1),B(3,1),C(3,3),D(1,3).
思考
新知学习
(1)分别作出点A,B,C,D关于x轴对称的对应点A1,B1,C1,D1,并写出它们的坐标;
A1
B1
C1
D1
A1( 1,-1),B1(3,-1),C1(3,-3),D1(1,-3)
你能说出点A与点A1坐标的关系吗?
横坐标相等,纵坐标互为相反数
已知点的坐标 A(l, 1) B(3, 1) C(3, 3) D(1,3)
关于x轴对称的点的坐标 A1(__,__ ) B1(__,__ ) C1(__,__ ) D1(__,__ )
1 -1
3 -1
3 -3
1 -3
总结:点(x,y)关于x轴对称的点的坐标为(x,-y),即横坐标不变,纵坐标互为相反数.
(2)分别作出点A,B,C,D关于y轴对称的对应点A,B,C,D,并写出它们的坐标.
已知点的坐标 A(l, 1) B(3, 1) C(3, 3) D(1,3)
关于y轴对称的点的坐标 A2(__,__ ) B2(__,__ ) C2(__,__ ) D2(__,__ )
-1 1
-3 1
-3 3
-1 3
A1
B1
C1
D1
总结:点(x,y)关于y轴对称的点的坐
标为(-x,y),即纵坐标不变,
横坐标互为相反数.
在平面直角坐标系中,
已知点P(x,y),它关于x轴对称的点的坐标为P1(___,___)
它关于y轴对称的点的坐标为P2(___,___).
x -y
-x y
归纳
如图,是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系.根据如图所示的东直门的坐标,现在你能说出西直门的坐标吗?
西直门(-3.5,4)
例1 如图,梯形ABCD关于y轴对称,点A的坐标为(-3,3),点B的坐标为(-2,0),写出点C和点D的坐标,并求出梯形ABCD的面积
解:点D与点A(-3,3)关于y轴对称.
∴点D的坐标为(3.3).
同理点C的坐标为(2,0).
∴AD=|3-(-3)|=6,BC=|2-(-2)|=4.
∴S梯形=
例2 已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点A、B关于x轴对称,求a、b的值;
(2)若A、B关于y轴对称,求(4a+b)2018的值.
解:(1)∵点A、B关于x轴对称,
∴2a-b=2b-1,5+a-a+b=0,
解得a=-8,b=-5;
(2)∵A、B关于y轴对称,
∴2a-b+2b-1=0,5+a=-a+b,
解得a=-1,b=3,
∴(4a+b)2018=1.
例3 平面直角坐标系中,△ABC 的三个顶点坐标分别为 A(0,4),B(2,4),C(3,-1).
(1)试在平面直角坐标系中,标出 A、B、C 三点;
x
y
O
A(0,4)
B(2,4)
C (3,-1)
(2)若△ABC 与△A'B'C' 关于 x 轴对称,画出△A'B'C',并写出 A'、B'、C' 的坐标.
x
y
O
A(0,4)
B(2,4)
C (3,-1)
A' (0,-4)
B'(2,-4)
C'(3,1)
对于这类问题,只要先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
在坐标系中作已知图形的对称图形
(一找二描三连)
分析:由关于y轴对称的点的坐标特征得m+2=5,
n+6=3,解得,m=3,n=-3.
1. 已知点A(m+2,3),B(-5,n+6)关于y轴对称,则m=________,
n=________.
3
-3
随堂练习
2.平面直角坐标系内的点A(-1,2)与点B(-1,-2)关于( )
A.y轴对称 B.x轴对称
C.原点对称 D.直线y=x对称
3.在平面直角坐标系中,将点A(-1,2)向右平移3个单位长度得到点
B,则点B关于x轴的对称点C的坐标是( )
A.(-4,-2) B.(2,2)
C.(-2,2) D.(2,-2)
D
B
4.如图,在平面直角坐标系中,点P(-1,2)关于直线x=1的对称点的坐标为( )
A.(1,2)
B.(2,2)
C.(3,2)
D.(4,2)
C
5.已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),
C(-1,3),作出△ABC关于y轴对称的图形.
解:点A(-3,5),B(-4,1),C(-1,3),
关于y轴的对称点分别为
A′(3,5),B′(4,1),C′(1,3).
依次连接A′B′,B′C′,C′A′,
就得到△ABC关于y轴对称的
△A′B′C′.
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
A
C
B
B ′
A′
C ′
x
y
在坐标系中
作关于坐标
轴对称的图形
点(x,y)关于x轴对称的点的坐标为(x,-y),即
横坐标相等,纵坐标互为相反数;
点(x,y)关于y轴对称的点的坐标为(-x,y),即
横坐标互为相反数,纵坐标相等.
先求出已知图形中的一些特殊点(如多边形的顶点)
的对应点的坐标,描出并连接这些点,就可以得到这
个图形的轴对称图形.(一找二描三连)
平面直角
坐标系中
的轴对称
关于坐标轴
对称的点的
坐标特征
课堂小结
