15.2线段的垂直平分线课件(共21张PPT)2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 15.2线段的垂直平分线课件(共21张PPT)2024-2025学年度八年级上册沪科版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 413.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-04 12:07:20 | ||
图片预览







文档简介
(共21张PPT)
沪科版
15.2 线段的垂直平分线
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.掌握线段的垂直平分线以及它的逆定理的条件和结论,学会应用到证明中;
2.经历探索线段的垂直平分线定理、逆定理的过程,明确应用方法.
学习目标
重点
根据之前所学知识,请你写出垂直平分线的定义
经过线段的中点并且垂直于这条线段的直线叫做这条线段的垂直平分线 ,又叫做线段的中垂线.
你知道如何作出线段的垂直平分线吗?
新课引入
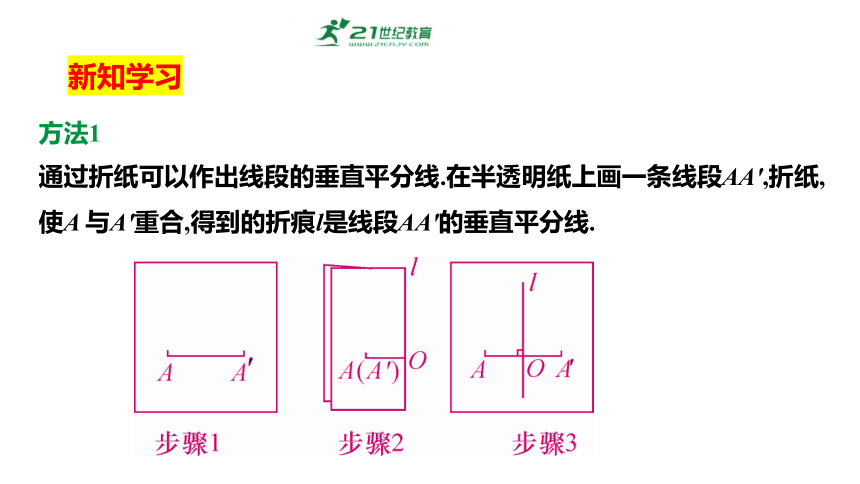
通过折纸可以作出线段的垂直平分线.在半透明纸上画一条线段AA',折纸,使A 与A'重合,得到的折痕l是线段AA'的垂直平分线.
方法1
新知学习
方法2
也可以用刻度尺量出线段的中点,再用三角尺过中点画垂线的方法作出线段的垂直平分线.
下面介绍用尺规作图,作出线段AB的垂直平分线.
作法:
则直线CD就是线段AB的垂直平分线.
2. 过点C,D作直线CD.
1.分别以点A,B为圆心, 大于 AB长为半径作弧,
两弧交于点C和D.
A
B
C
D
为什么这样作出的直线CD,就是线段AB的垂直平分线呢 设所作直线CD交AB于点О,你能给出证明吗
A
B
C
D
证:设CD与AB相交于点E
在△ACD和△BCD中
AC=BC
AD=BD
CD=CD
∴△ACD ≌△BCD(SSS)
∴∠ACD=∠BCD
∴CD是AB的垂直平分线
E
AC=BC
∠ACD=∠BCD
CE=CE
∴△ACE ≌△BCE(SAS)
∴∠AEC=∠BEC=90°
∴AO=BO
∴AB⊥CD
PA=PB
P1A=P1B
……
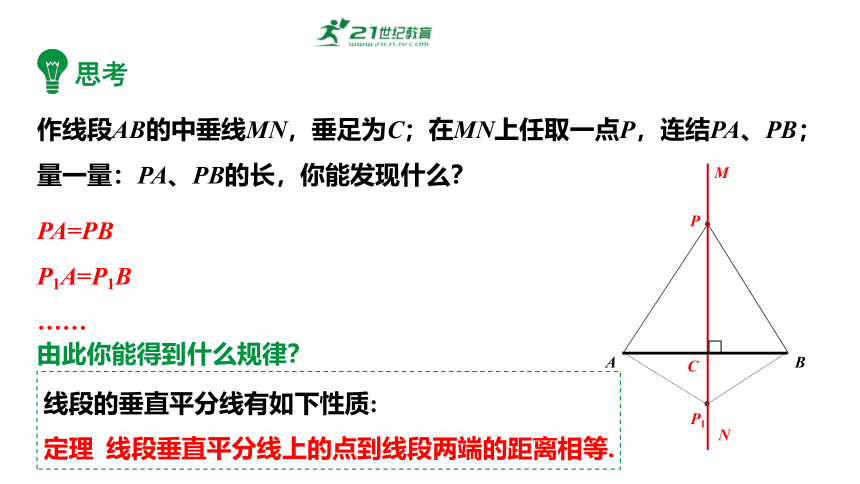
作线段AB的中垂线MN,垂足为C;在MN上任取一点P,连结PA、PB;
量一量:PA、PB的长,你能发现什么?
由此你能得到什么规律?
思考
A
B
P1
P
M
N
C
线段的垂直平分线有如下性质:
定理 线段垂直平分线上的点到线段两端的距离相等.
A
B
P
M
N
O
例1:如图直线MN经过AB的中点O,且MN⊥AB, P是MN上任意一点上.
求证:PA=PB.
证明:∵MN⊥AB
∴ ∠POA= ∠BOP=90
在 ΔAOP和Δ BOP中,
AO=BO
∠AOP=∠BOP
PO=PO
∴ ΔAOP ≌Δ BOP (SAS)
∴PA=PB
例2 如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,求BC的长.
解:∵DE垂直平分AB,
∴AD=BD
∵△DBC的周长为BC+BD+CD=35(cm),
∴ BC+AD+CD=35cm.
∵AC=AD+DC=20cm,
∴BC=35-20=15(cm).
你能写出上面定理的逆命题吗 它是真命题吗 如果是真命题,请给出证明.
思考
定理 到线段两端距离相等的点在线段的垂直平分线上.
证明:
如图,过点P作 PO⊥ AB,垂足为点O,
在△PAO和△PBO,因为∠POA =∠POB=90°
△PAO≌△PBO,因此 AO=BO,即PO是线段AB的垂直平分线.
A
B
P
M
N
O
证明:连接PA,PB,PC.
∵点P在AB, AC的垂直平分线上,(已知)
∴PA = PB, PA = PC.
(线段垂直平分线上的点到线段两端的距离相等)
∴PB = PC.(等量代换)
∴点P在BC的垂直平分线上.
(到线段两端距离相等的点在线段的垂直平分线上)
例3 已知:如图,△ABC的边AB, AC的垂直平分线相交于点P.
求证:点P在BC的垂直平分线上.
归纳
这个例子说明:三角形三边的垂直平分线相交于一点,这点到三角形三个顶点的距离相等.
例4 如图,有A,B,C三个村庄,现准备要建一所自来水厂,要求自来水厂到三个村庄的距离相等,请你确定自来水厂的位置.
B
C
A
解:由题意可知,水厂应建在连接任意两点的两条线段的垂直平分线的交点处.
1.如图,在△ABC中,分别以点A,B为圆心,大于 AB长为半径画弧,两弧分别交于点D,E,则直线DE是( )
A.∠A的平分线
B.AC边的中线
C.BC边的高线
D.AB边的垂直平分线
D
随堂练习
B
2.如图,直线CD是线段AB的垂直平分线,P为直线CD 上的一点,已知线段PA=5,则线段PB的长度为( ).
A.6 B.5 C.4 D.3
3.如图,OC是∠AOB的平分线,AC⊥AO, BC⊥BO,则OC与AB的关系是( ).
A. AB垂直平分OC
B. OC垂直平分AB
C. OC只平分AB但不平分
D. OC只垂直AB但不平分
B
4.下列说法错误的是( )
A.点D,E在线段AB垂直平分线上,则AD=BD,AE=BE
B.若AD=BD,AE=BE,则DE是线段AB的垂直平分线
C.若PA=PB,则点P在线段AB的垂直平分线上
D.若PA=PB,则过点P的直线是AB的垂直平分线
D
5.如图,△ABC中,AB=AC,AB的垂直平分线交AC于E,连接BE,AB+BC=16cm,则△BCE的周长是 cm.
16
A
B
C
D
E
6.已知:如图,点C,D是线段AB外的两点,且AC =BC, AD=BD,AB与CD相交于点O.
求证:AO=BO.
证明: ∵ AC =BC,AD=BD,
∴
点C和点D在线段AB的垂直平分线上,
∴ CD为线段AB的垂直平分线.
又 ∵AB与CD相交于点O,
∴
AO=BO.
判定
线段的垂直平分线上的点到线段的两个端点的距离相等
到线段的两个端点距离相等的点在线段的垂直平分线上
线段的
垂直平分线
性质
课堂小结
沪科版
15.2 线段的垂直平分线
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.掌握线段的垂直平分线以及它的逆定理的条件和结论,学会应用到证明中;
2.经历探索线段的垂直平分线定理、逆定理的过程,明确应用方法.
学习目标
重点
根据之前所学知识,请你写出垂直平分线的定义
经过线段的中点并且垂直于这条线段的直线叫做这条线段的垂直平分线 ,又叫做线段的中垂线.
你知道如何作出线段的垂直平分线吗?
新课引入
通过折纸可以作出线段的垂直平分线.在半透明纸上画一条线段AA',折纸,使A 与A'重合,得到的折痕l是线段AA'的垂直平分线.
方法1
新知学习
方法2
也可以用刻度尺量出线段的中点,再用三角尺过中点画垂线的方法作出线段的垂直平分线.
下面介绍用尺规作图,作出线段AB的垂直平分线.
作法:
则直线CD就是线段AB的垂直平分线.
2. 过点C,D作直线CD.
1.分别以点A,B为圆心, 大于 AB长为半径作弧,
两弧交于点C和D.
A
B
C
D
为什么这样作出的直线CD,就是线段AB的垂直平分线呢 设所作直线CD交AB于点О,你能给出证明吗
A
B
C
D
证:设CD与AB相交于点E
在△ACD和△BCD中
AC=BC
AD=BD
CD=CD
∴△ACD ≌△BCD(SSS)
∴∠ACD=∠BCD
∴CD是AB的垂直平分线
E
AC=BC
∠ACD=∠BCD
CE=CE
∴△ACE ≌△BCE(SAS)
∴∠AEC=∠BEC=90°
∴AO=BO
∴AB⊥CD
PA=PB
P1A=P1B
……
作线段AB的中垂线MN,垂足为C;在MN上任取一点P,连结PA、PB;
量一量:PA、PB的长,你能发现什么?
由此你能得到什么规律?
思考
A
B
P1
P
M
N
C
线段的垂直平分线有如下性质:
定理 线段垂直平分线上的点到线段两端的距离相等.
A
B
P
M
N
O
例1:如图直线MN经过AB的中点O,且MN⊥AB, P是MN上任意一点上.
求证:PA=PB.
证明:∵MN⊥AB
∴ ∠POA= ∠BOP=90
在 ΔAOP和Δ BOP中,
AO=BO
∠AOP=∠BOP
PO=PO
∴ ΔAOP ≌Δ BOP (SAS)
∴PA=PB
例2 如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,求BC的长.
解:∵DE垂直平分AB,
∴AD=BD
∵△DBC的周长为BC+BD+CD=35(cm),
∴ BC+AD+CD=35cm.
∵AC=AD+DC=20cm,
∴BC=35-20=15(cm).
你能写出上面定理的逆命题吗 它是真命题吗 如果是真命题,请给出证明.
思考
定理 到线段两端距离相等的点在线段的垂直平分线上.
证明:
如图,过点P作 PO⊥ AB,垂足为点O,
在△PAO和△PBO,因为∠POA =∠POB=90°
△PAO≌△PBO,因此 AO=BO,即PO是线段AB的垂直平分线.
A
B
P
M
N
O
证明:连接PA,PB,PC.
∵点P在AB, AC的垂直平分线上,(已知)
∴PA = PB, PA = PC.
(线段垂直平分线上的点到线段两端的距离相等)
∴PB = PC.(等量代换)
∴点P在BC的垂直平分线上.
(到线段两端距离相等的点在线段的垂直平分线上)
例3 已知:如图,△ABC的边AB, AC的垂直平分线相交于点P.
求证:点P在BC的垂直平分线上.
归纳
这个例子说明:三角形三边的垂直平分线相交于一点,这点到三角形三个顶点的距离相等.
例4 如图,有A,B,C三个村庄,现准备要建一所自来水厂,要求自来水厂到三个村庄的距离相等,请你确定自来水厂的位置.
B
C
A
解:由题意可知,水厂应建在连接任意两点的两条线段的垂直平分线的交点处.
1.如图,在△ABC中,分别以点A,B为圆心,大于 AB长为半径画弧,两弧分别交于点D,E,则直线DE是( )
A.∠A的平分线
B.AC边的中线
C.BC边的高线
D.AB边的垂直平分线
D
随堂练习
B
2.如图,直线CD是线段AB的垂直平分线,P为直线CD 上的一点,已知线段PA=5,则线段PB的长度为( ).
A.6 B.5 C.4 D.3
3.如图,OC是∠AOB的平分线,AC⊥AO, BC⊥BO,则OC与AB的关系是( ).
A. AB垂直平分OC
B. OC垂直平分AB
C. OC只平分AB但不平分
D. OC只垂直AB但不平分
B
4.下列说法错误的是( )
A.点D,E在线段AB垂直平分线上,则AD=BD,AE=BE
B.若AD=BD,AE=BE,则DE是线段AB的垂直平分线
C.若PA=PB,则点P在线段AB的垂直平分线上
D.若PA=PB,则过点P的直线是AB的垂直平分线
D
5.如图,△ABC中,AB=AC,AB的垂直平分线交AC于E,连接BE,AB+BC=16cm,则△BCE的周长是 cm.
16
A
B
C
D
E
6.已知:如图,点C,D是线段AB外的两点,且AC =BC, AD=BD,AB与CD相交于点O.
求证:AO=BO.
证明: ∵ AC =BC,AD=BD,
∴
点C和点D在线段AB的垂直平分线上,
∴ CD为线段AB的垂直平分线.
又 ∵AB与CD相交于点O,
∴
AO=BO.
判定
线段的垂直平分线上的点到线段的两个端点的距离相等
到线段的两个端点距离相等的点在线段的垂直平分线上
线段的
垂直平分线
性质
课堂小结
