2024-2025学年北师大版九年级数学上册 1.2矩形的性质与判定第2课时 矩形的判定 课件(共32张PPT)
文档属性
| 名称 | 2024-2025学年北师大版九年级数学上册 1.2矩形的性质与判定第2课时 矩形的判定 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-04 12:50:55 | ||
图片预览







文档简介
(共32张PPT)
北师大版九年级数学上册课件
第一章 特殊平行四边形
1.2 矩形的性质与判定
第2课时 矩形的判定
探索并证明矩形的判定定理:三个角是直角的四边形是矩形,对角线相等的平行四边形是矩形.
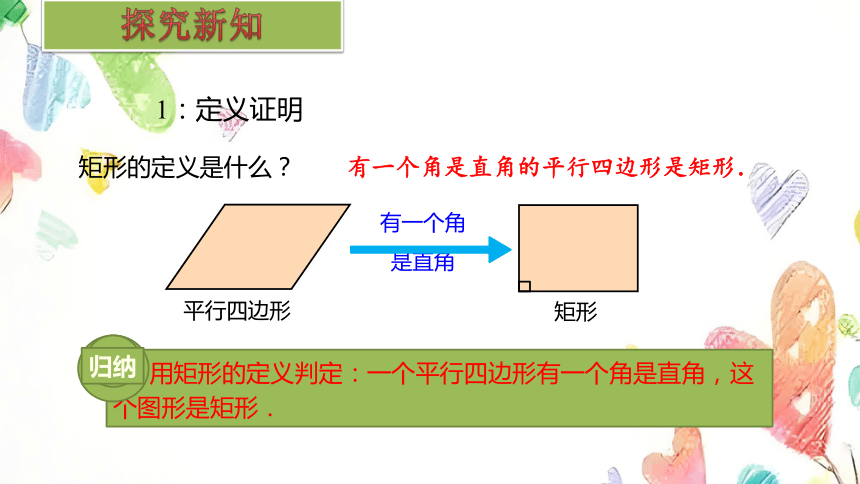
1:定义证明
矩形的定义是什么?
有一个角是直角的平行四边形是矩形.
有一个角
是直角
平行四边形
矩形
用矩形的定义判定:一个平行四边形有一个角是直角,这个图形是矩形.
归纳
探究新知
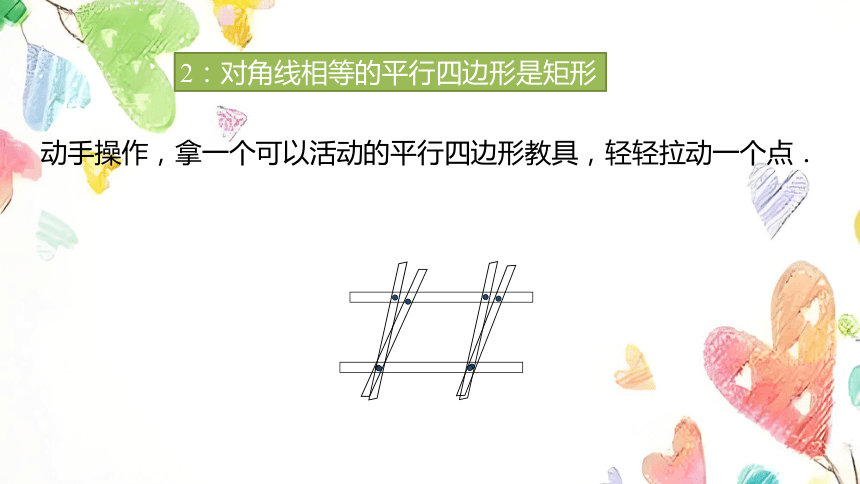
2:对角线相等的平行四边形是矩形
动手操作,拿一个可以活动的平行四边形教具,轻轻拉动一个点.
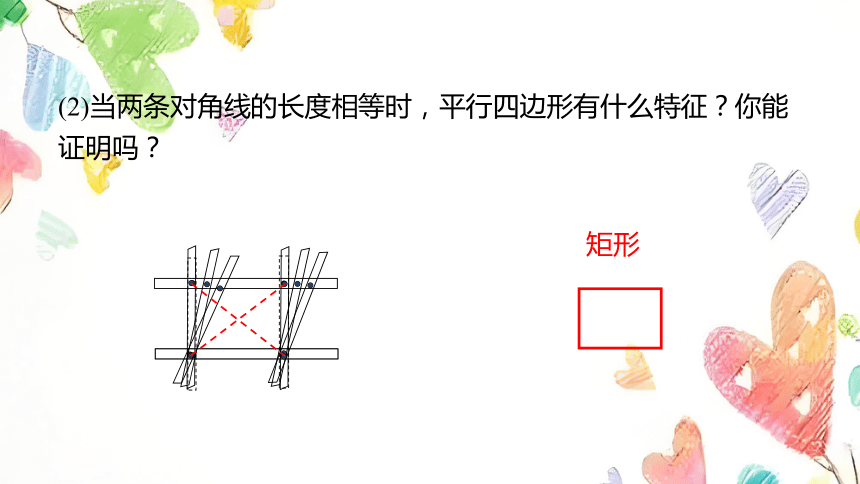
(2)当两条对角线的长度相等时,平行四边形有什么特征?你能证明吗?
矩形
归纳总结
矩形的判定1:
定理:对角线相等的平行四边形是矩形.
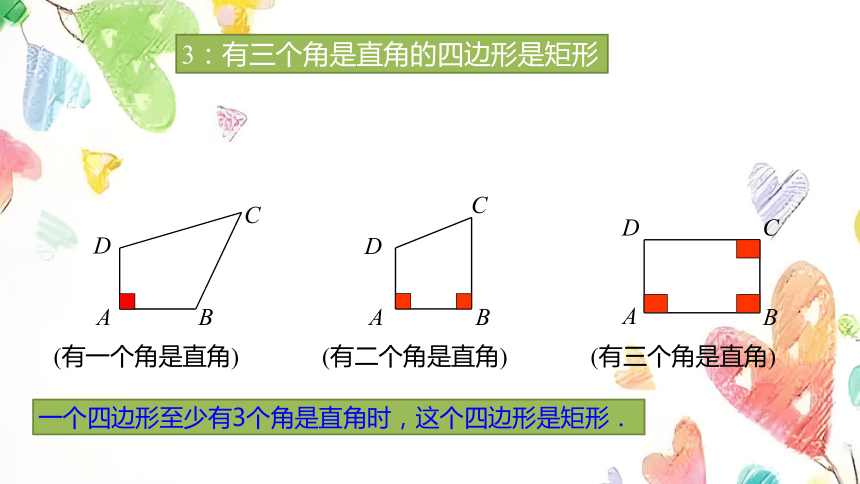
一个四边形至少有3个角是直角时,这个四边形是矩形.
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
3:有三个角是直角的四边形是矩形
归纳总结
矩形的判定2:
定理:有三个角是直角的四边形是矩形.
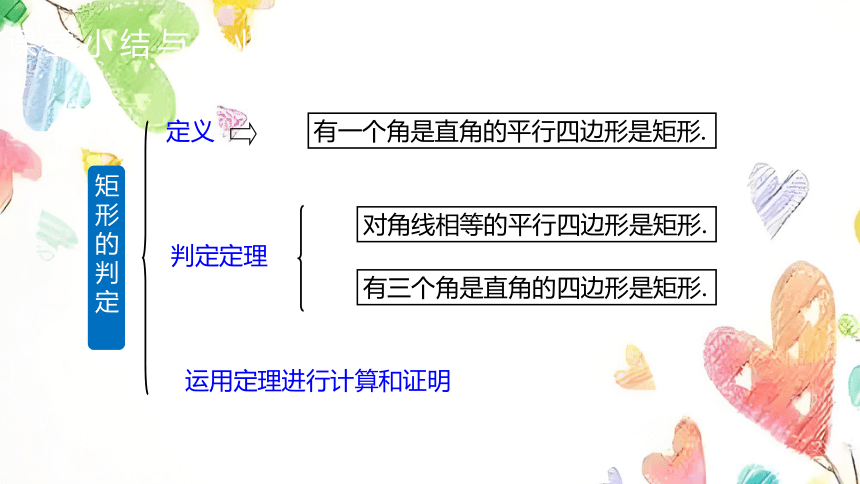
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
运用定理进行计算和证明
定义
判定定理
矩形的判定
课堂小结与作业
1.有一个角是______的平行四边形是矩形.
2.对角线______的平行四边形是矩形.
3.有三个角是______的四边形是矩形.
直角
相等
直角
知识点一 由平行四边形证明矩形
1.下列说法中正确的是( )
D
A.有一个角是直角的四边形是矩形
B.四边相等的四边形是矩形
C.对角线互相垂直的平行四边形是矩形
D.对角线相等的平行四边形是矩形
(第2题图)
2.如图,在 中, , 是 上
两点, ,连接 , ,
, ,添加一个条件,能判定四边形
是矩形的是( )
B
A. B.
C. D.
(第3题图)
3.如图,在 中,对角线 , 相交于点
,且 , ,则 的度数
为( )
A
A. B. C. D.
4.如图,点 是 的中点,四边形 是平行四
边形.若 ,求证:四边形 是矩形.
证明: 四边形 是平行四边形,
,且 , .
点 是 的中点,
.
, 四边形 是平行四边形.
, .
四边形 是矩形.
知识点二 有三个角是直角的四边形是矩形
5.如图,过 的顶点 分别作 及其邻
补角的平分线的垂线,垂足分别为 , ,求证:
四边形 是矩形.
证明: 平分 , 平分 ,
, .
,
,
即 .
又 , ,
.
四边形 是矩形.
易错点 菱形的判定与矩形的判定相互混淆
6.已知平行四边形 的对角线 与 相交于点 ,下列结论中
不正确的是( )
D
A.当 时,四边形 是矩形
B.当 时,四边形 是菱形
C.当 时,四边形 是矩形
D.当 时,四边形 是菱形
(第7题图)
7.如图,在 中, ,
.连接 ,过点 作 ,
交 的延长线于点 ,连接 ,交 于
点 .若 ,则四边形
的面积为_ ____.
(第8题图)
8.如图,直线 与 轴交于点 ,
与 轴交于点 ,点 为线段 上的一个动点,
作 轴于点 , 轴于点 ,连接
,则线段 长的最小值为_ ___.
9.如图,在 中,各个内角的平分线相交于
点 , , , ,连接 , .
(1) 猜想 与 之间的关系;
(2) 请证明你的猜想.
(1) 猜想 与 之间的关系;
解: .
(2) 请证明你的猜想.
证明: 四边形 是平行四边形,
, .
.
又 , 分别平分 , ,
.
.
同理可证 , ,
四边形 为矩形.
.
10.如图,菱形 的对角线 , 相交
于点 ,过点 作 ,且 ,
连接 .
(1) 求证:四边形 为矩形.
(2) 连接 ,若 , ,求 的长.
(1) 求证:四边形 为矩形.
证明: 四边形 是菱形,
, .
.
, ,
, .
四边形 是平行四边形.
又 ,
平行四边形 是矩形.
(2) 连接 ,若 , ,求 的长.
解: 四边形 是菱形,
.
由(1)得四边形 为矩形,
, .
在 中,由勾股定理得
,
即 的长为 .
完成学生用书对应课时练习
谢谢大家欣赏
北师大版九年级数学上册课件
第一章 特殊平行四边形
1.2 矩形的性质与判定
第2课时 矩形的判定
探索并证明矩形的判定定理:三个角是直角的四边形是矩形,对角线相等的平行四边形是矩形.
1:定义证明
矩形的定义是什么?
有一个角是直角的平行四边形是矩形.
有一个角
是直角
平行四边形
矩形
用矩形的定义判定:一个平行四边形有一个角是直角,这个图形是矩形.
归纳
探究新知
2:对角线相等的平行四边形是矩形
动手操作,拿一个可以活动的平行四边形教具,轻轻拉动一个点.
(2)当两条对角线的长度相等时,平行四边形有什么特征?你能证明吗?
矩形
归纳总结
矩形的判定1:
定理:对角线相等的平行四边形是矩形.
一个四边形至少有3个角是直角时,这个四边形是矩形.
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
3:有三个角是直角的四边形是矩形
归纳总结
矩形的判定2:
定理:有三个角是直角的四边形是矩形.
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
运用定理进行计算和证明
定义
判定定理
矩形的判定
课堂小结与作业
1.有一个角是______的平行四边形是矩形.
2.对角线______的平行四边形是矩形.
3.有三个角是______的四边形是矩形.
直角
相等
直角
知识点一 由平行四边形证明矩形
1.下列说法中正确的是( )
D
A.有一个角是直角的四边形是矩形
B.四边相等的四边形是矩形
C.对角线互相垂直的平行四边形是矩形
D.对角线相等的平行四边形是矩形
(第2题图)
2.如图,在 中, , 是 上
两点, ,连接 , ,
, ,添加一个条件,能判定四边形
是矩形的是( )
B
A. B.
C. D.
(第3题图)
3.如图,在 中,对角线 , 相交于点
,且 , ,则 的度数
为( )
A
A. B. C. D.
4.如图,点 是 的中点,四边形 是平行四
边形.若 ,求证:四边形 是矩形.
证明: 四边形 是平行四边形,
,且 , .
点 是 的中点,
.
, 四边形 是平行四边形.
, .
四边形 是矩形.
知识点二 有三个角是直角的四边形是矩形
5.如图,过 的顶点 分别作 及其邻
补角的平分线的垂线,垂足分别为 , ,求证:
四边形 是矩形.
证明: 平分 , 平分 ,
, .
,
,
即 .
又 , ,
.
四边形 是矩形.
易错点 菱形的判定与矩形的判定相互混淆
6.已知平行四边形 的对角线 与 相交于点 ,下列结论中
不正确的是( )
D
A.当 时,四边形 是矩形
B.当 时,四边形 是菱形
C.当 时,四边形 是矩形
D.当 时,四边形 是菱形
(第7题图)
7.如图,在 中, ,
.连接 ,过点 作 ,
交 的延长线于点 ,连接 ,交 于
点 .若 ,则四边形
的面积为_ ____.
(第8题图)
8.如图,直线 与 轴交于点 ,
与 轴交于点 ,点 为线段 上的一个动点,
作 轴于点 , 轴于点 ,连接
,则线段 长的最小值为_ ___.
9.如图,在 中,各个内角的平分线相交于
点 , , , ,连接 , .
(1) 猜想 与 之间的关系;
(2) 请证明你的猜想.
(1) 猜想 与 之间的关系;
解: .
(2) 请证明你的猜想.
证明: 四边形 是平行四边形,
, .
.
又 , 分别平分 , ,
.
.
同理可证 , ,
四边形 为矩形.
.
10.如图,菱形 的对角线 , 相交
于点 ,过点 作 ,且 ,
连接 .
(1) 求证:四边形 为矩形.
(2) 连接 ,若 , ,求 的长.
(1) 求证:四边形 为矩形.
证明: 四边形 是菱形,
, .
.
, ,
, .
四边形 是平行四边形.
又 ,
平行四边形 是矩形.
(2) 连接 ,若 , ,求 的长.
解: 四边形 是菱形,
.
由(1)得四边形 为矩形,
, .
在 中,由勾股定理得
,
即 的长为 .
完成学生用书对应课时练习
谢谢大家欣赏
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
