人教版六年级上册数学圆的周长和面积课件(共31张PPT)
文档属性
| 名称 | 人教版六年级上册数学圆的周长和面积课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-04 11:04:37 | ||
图片预览










文档简介
(共31张PPT)
第十讲:圆的周长和面积初步
本讲聚焦
1、半径、直径和圆周率之间的关系
2、圆的周长与面积计算
3. 圆的周长与面积应用
01
半径、直径
和圆周率
PART.01
√
×
×
√
×
×
(注:对称轴是直线,而直径是线段)(直径所在的直线是圆的对称轴)
(π是一个无限不循环小数)
(要在同一个圆内才能比较)
C = 2πr C÷r = 2π (固定)
(C半圆 = 圆周长一半 + 1条直径 C半圆 = πr + 2r = 5.14r )
【半径、直径和圆周率的特征及关系】
例题1:判断
①直径是圆里最长的线段。( )
②直径比半径长。( )
③直径是圆的对称轴,圆有无数条直径,所以圆有无数条对称轴。( )
④ ( )
⑤大小不同的两个圆,它们的周长与半径的比值是相等的。( )
⑥半圆的周长等于与它半径相同圆的周长的一半( )
圆的周长及面积计算
PART.02
练习1:
【圆的周长及面积计算】
圆的周长:C圆=( )或C圆=( );
半圆的周长:C半圆=( );
圆的面积:S圆=( );
圆环的面积:S圆环=( )。
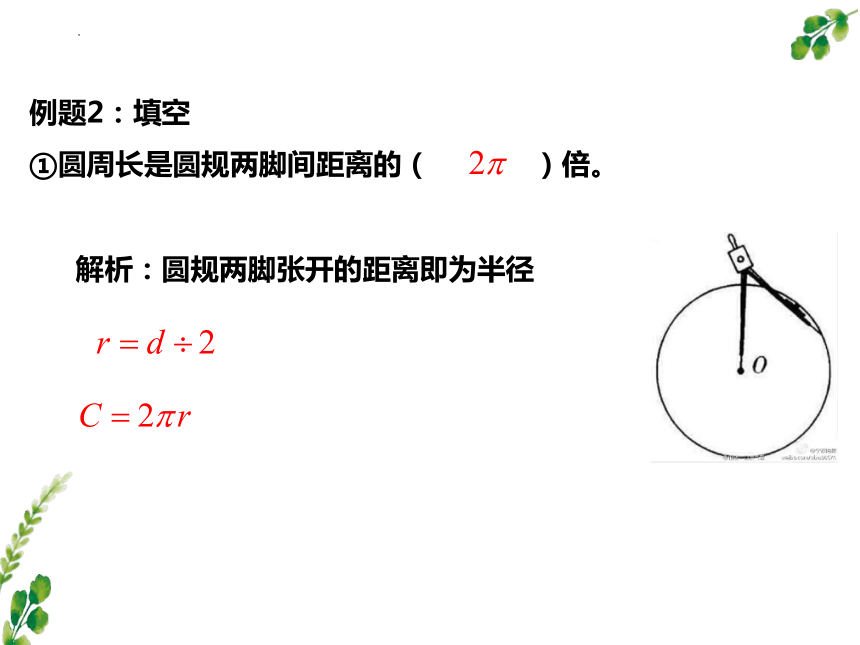
解析:圆规两脚张开的距离即为半径
例题2:填空
①圆周长是圆规两脚间距离的( )倍。
②自行车的轮胎直径是0.8米,如果每分钟转50周,十分钟可以行( )米。
1256
解析:车轮转动一周即前进一周的距离。
轮胎周长:3.14×0.8=2.512(米)
每分钟转50周,十分钟转:10×50=500(周)
十分钟可行:2.512×500=1256(米)
③一个圆形花坛,周长25.12米。周围修一条1米宽的小路,小路的面积是( )平方米。
28.26
r : 25.12÷3.14÷2 = 4 (m)
R : 4+1 = 5 (m)
S圆环:3.14×(52-42)=
r=4
1
解析:圆环面积公式 :
R=4+1
3.14×(25 — 16)
= 3.14×9
= 28.26(m2)
④两个圆的半径比是3:4,周长比是( ),面积比是( )。
3:4
9:16
结论:周长比=半径比=直径比 面积比=半径的平方比
解析:假设两个圆的半径分别是3和4,
⑤面积为6.28平方厘米的半圆片,半径是( )厘米,周长是( )厘米。
10.28
2
r2:12.56÷3.14 = 4(cm2)
r = 2(cm)
= 5.14×2 = 10.28(cm)
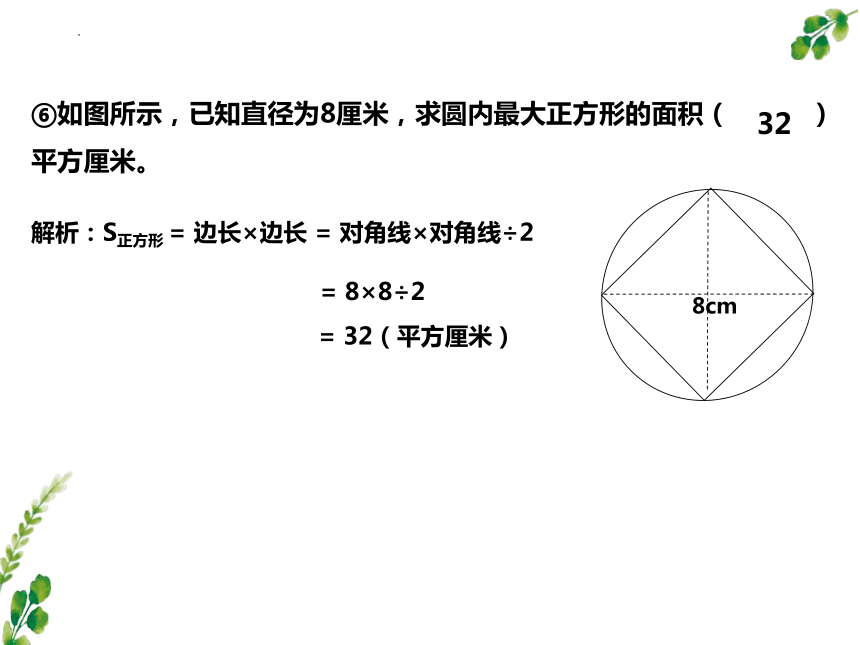
⑥如图所示,已知直径为8厘米,求圆内最大正方形的面积( )平方厘米。
8cm
= 8×8÷2
= 32(平方厘米)
32
解析:S正方形 = 边长×边长 = 对角线×对角线÷2
⑦
亮亮用一张长20厘米,宽12厘米的的长方形硬纸板剪半径为5厘米的圆,他最多能剪( )个。
解析:r = 5cm,则 d = 10cm
长有几个直径: 20÷10=2(个),
宽有几个直径:12÷10=1(个)...2(厘米)
共有几个圆: 2×1=2(个)
所以最多能剪2个
20厘米
12厘米
2
⑧周长相等的正方形、长方形和圆,面积最大的是( );
若面积相等中周长最大的是 ( )。
长方形
圆
结论:面积相等的正方形,长方形,圆中,周长最大的是长方形。
假设正方形、长方形和圆形的周长都是16,
则圆的面积为: ;
正方形的边长为:16÷4=4,面积为:4×4=16;
长方形长宽越接近面积越大,就取长为5宽为3,面积为:5×3=15,
当长方形的长和宽最接近时面积也小于16;
结论 : 周长相等的正方形、长方形和圆形,圆面积最大。
由圆的面积公式推导,可知,把圆无限切分近似组合为一个长方形,
其面积和圆面积相等,周长比圆的周长多一条直径。
所以:面积相等的长方形和圆,长方形的周长大于圆的周长。
面积相等的正方形和长方形:假设正方形的边长为6;
长方形的长为9,宽为4;它们的面积都为36。
则正方形周长:4×6=24,
长方形周长:(4+9)×2=26。
所以:面积相等正方形和长方形,长方形的周长大于正方形的周长。
03
圆面积和周长应用
PART.03
【圆面积和周长运用】
例题3:把圆转化成近似的长方形后,形状发生改变,面积不变。
长方形的长相当于圆的( ),
长方形的宽相当于圆的( ),
长方形的周长比圆的周长多了( )。如果圆的半径用r表示,则长方形的宽用( )表示,
长用( )表示。长方形的面积 = 长 × 宽 ,所以:S =( ) ×( )。
周长的一半
半径
2条半径
或 1条直径
练习3:圆面积公式的推导有不同的方法。有一个同学是这样做的:把圆平均分成4份、9份、16份、25份……得到若干个大小相同的小扇形,再把小扇形拼成一个近似的三角形(份数分的越多,拼成的图形越接近三角形)。
如右图是把圆平均分成9份后拼成的图形。如果圆的半径用r表示,
那么三角形的底可以表示成( )则三角形的面积是( ),由此可得到圆的面积是( )。
例题4:一个挂钟时针长5厘米,则时针尖端一昼夜所走的路程是多少米,所扫过的面积是多少平方厘米?
1圈路程:C=3.14×5×2 = 31.4(cm)
所走路程:31.4×2 = 62.8(cm) =0.628(m)
1圈面积:S=3.14×52 = 78.5(cm2)
扫过面积:78.5×2 = 157(平方厘米)
r = 5cm
24小时 = 时针转2圈
练习4:一个钟表的分针长30厘米,从上午9点10分到9点50分,分针针尖走过的路程是多少厘米?扫过的面积是多少平方厘米?
解析:
从9点10分到9点50分,分针走了40分钟,一圈60分钟,分针走了
1圈的周长:3.14×30×2=188.4(厘米)
1圈的面积:3.14×30×30=2826(平方厘米)
半径长
04
综合巩固
综合巩固
①半径为2厘米的圆,半径增加1厘米后,它的面积增加( )
平方厘米。
解析:增加的面积即为圆环的面积。
r=2(厘米),R=2+1=3(厘米)
3.14×(32-22)=15.7(平方厘米)
15.7
②一个圆的面积为28.26平方厘米,这个圆的半径是( ) 厘米。
解析:
3
③半圆的周长为10.28厘米,它的面积为( )平方厘米。
S半圆 = 3.14 ×22÷2 = 6.28(cm2)
解析:
6.28
④如图,明星学校有一个运动场,运动场的中间是长方形,长方形的长是60米,宽是40米,两头是半圆形。求出它的周长( )米,面积( )平方米。
解析:周长 = C圆 + 50×2
面积 = S圆 + S长
60米
40米
面积:3.14×20×20 + 40×60 = 3656 (平方米)
r:40÷2 = 20 (米)
周长:3.14×40 + 60×2 = 245.6 (米)
245.6
3256
⑤一种自行车的前齿轮齿数是45,后轮齿数是15,后轮直径是60厘米,如果前轮转动两周,自行车大约前进( )米。
分析:前轮走的路程等于后轮走的路程
前轮齿数×圈数=后轮齿数×圈数
45×2 ÷ 15 = 6(周)
所以:前轮转动2周,后轮转动6周
自行车大约前进:3.14×60×6 = 1130.4cm = 11.304m
11.304
⑥直径是1.6米的圆形餐桌,高1米,上面铺了一块正方形台布,台布的四个角正好触到地面,这块台布的面积是( )平方米。
桌布对角线长度 = 1.6+1+1=3.6(米)
1.6
1
1
S正 = 对角线×对角线÷2
= 3.6×3.6÷2
= 6.48(平方米)
结论:正方形的面积 = 边长×边长 = 对角线×对角线÷2
6.48
⑦把一个圆平均分成2018个小扇形后,拼成一个近似的长方形,周长比原来增加了8厘米,求这个圆的面积是( )。
解析:拼成近似的长方形,面积不变,周长增加两条半径
r : 8÷2 = 4(厘米)
S : 3.14×42 = 50.24(平方厘米)
50.24平方厘米
⑧如图,三个相同的圆面积都是18平方厘米,求阴影部分的面积和是多少?
解析:
三个圆面积相同 三个圆的 r 相同。
∠A+∠B+∠C = 1800
可知:三个阴影部分面积之和 = 半圆的面积
S阴 = 18÷2 = 9(cm2)
⑧如图,大圆的直径是小圆直径的 倍,如果阴影部分的面积是 65 平方厘米, 那么小圆的面积是( )平方厘米。
16
⑨石头落到水中,平静水面产生的许多圆形波纹叫涟漪。
(1)设波纹以每秒 1 米的速度向四周扩散,试求 2 秒后波纹的面积?
(2)如果每秒产生一个新的波纹,并且后面的波纹以相同的速度向四周扩散。石头落到水中 3 秒后,产生的第一个波纹比第二个波纹的面积大多少平方米?
(1)分析:此时波纹形成了一个半径为2米的圆
(2)分析:根据题意求圆环的面积
THANKS
第十讲:圆的周长和面积初步
本讲聚焦
1、半径、直径和圆周率之间的关系
2、圆的周长与面积计算
3. 圆的周长与面积应用
01
半径、直径
和圆周率
PART.01
√
×
×
√
×
×
(注:对称轴是直线,而直径是线段)(直径所在的直线是圆的对称轴)
(π是一个无限不循环小数)
(要在同一个圆内才能比较)
C = 2πr C÷r = 2π (固定)
(C半圆 = 圆周长一半 + 1条直径 C半圆 = πr + 2r = 5.14r )
【半径、直径和圆周率的特征及关系】
例题1:判断
①直径是圆里最长的线段。( )
②直径比半径长。( )
③直径是圆的对称轴,圆有无数条直径,所以圆有无数条对称轴。( )
④ ( )
⑤大小不同的两个圆,它们的周长与半径的比值是相等的。( )
⑥半圆的周长等于与它半径相同圆的周长的一半( )
圆的周长及面积计算
PART.02
练习1:
【圆的周长及面积计算】
圆的周长:C圆=( )或C圆=( );
半圆的周长:C半圆=( );
圆的面积:S圆=( );
圆环的面积:S圆环=( )。
解析:圆规两脚张开的距离即为半径
例题2:填空
①圆周长是圆规两脚间距离的( )倍。
②自行车的轮胎直径是0.8米,如果每分钟转50周,十分钟可以行( )米。
1256
解析:车轮转动一周即前进一周的距离。
轮胎周长:3.14×0.8=2.512(米)
每分钟转50周,十分钟转:10×50=500(周)
十分钟可行:2.512×500=1256(米)
③一个圆形花坛,周长25.12米。周围修一条1米宽的小路,小路的面积是( )平方米。
28.26
r : 25.12÷3.14÷2 = 4 (m)
R : 4+1 = 5 (m)
S圆环:3.14×(52-42)=
r=4
1
解析:圆环面积公式 :
R=4+1
3.14×(25 — 16)
= 3.14×9
= 28.26(m2)
④两个圆的半径比是3:4,周长比是( ),面积比是( )。
3:4
9:16
结论:周长比=半径比=直径比 面积比=半径的平方比
解析:假设两个圆的半径分别是3和4,
⑤面积为6.28平方厘米的半圆片,半径是( )厘米,周长是( )厘米。
10.28
2
r2:12.56÷3.14 = 4(cm2)
r = 2(cm)
= 5.14×2 = 10.28(cm)
⑥如图所示,已知直径为8厘米,求圆内最大正方形的面积( )平方厘米。
8cm
= 8×8÷2
= 32(平方厘米)
32
解析:S正方形 = 边长×边长 = 对角线×对角线÷2
⑦
亮亮用一张长20厘米,宽12厘米的的长方形硬纸板剪半径为5厘米的圆,他最多能剪( )个。
解析:r = 5cm,则 d = 10cm
长有几个直径: 20÷10=2(个),
宽有几个直径:12÷10=1(个)...2(厘米)
共有几个圆: 2×1=2(个)
所以最多能剪2个
20厘米
12厘米
2
⑧周长相等的正方形、长方形和圆,面积最大的是( );
若面积相等中周长最大的是 ( )。
长方形
圆
结论:面积相等的正方形,长方形,圆中,周长最大的是长方形。
假设正方形、长方形和圆形的周长都是16,
则圆的面积为: ;
正方形的边长为:16÷4=4,面积为:4×4=16;
长方形长宽越接近面积越大,就取长为5宽为3,面积为:5×3=15,
当长方形的长和宽最接近时面积也小于16;
结论 : 周长相等的正方形、长方形和圆形,圆面积最大。
由圆的面积公式推导,可知,把圆无限切分近似组合为一个长方形,
其面积和圆面积相等,周长比圆的周长多一条直径。
所以:面积相等的长方形和圆,长方形的周长大于圆的周长。
面积相等的正方形和长方形:假设正方形的边长为6;
长方形的长为9,宽为4;它们的面积都为36。
则正方形周长:4×6=24,
长方形周长:(4+9)×2=26。
所以:面积相等正方形和长方形,长方形的周长大于正方形的周长。
03
圆面积和周长应用
PART.03
【圆面积和周长运用】
例题3:把圆转化成近似的长方形后,形状发生改变,面积不变。
长方形的长相当于圆的( ),
长方形的宽相当于圆的( ),
长方形的周长比圆的周长多了( )。如果圆的半径用r表示,则长方形的宽用( )表示,
长用( )表示。长方形的面积 = 长 × 宽 ,所以:S =( ) ×( )。
周长的一半
半径
2条半径
或 1条直径
练习3:圆面积公式的推导有不同的方法。有一个同学是这样做的:把圆平均分成4份、9份、16份、25份……得到若干个大小相同的小扇形,再把小扇形拼成一个近似的三角形(份数分的越多,拼成的图形越接近三角形)。
如右图是把圆平均分成9份后拼成的图形。如果圆的半径用r表示,
那么三角形的底可以表示成( )则三角形的面积是( ),由此可得到圆的面积是( )。
例题4:一个挂钟时针长5厘米,则时针尖端一昼夜所走的路程是多少米,所扫过的面积是多少平方厘米?
1圈路程:C=3.14×5×2 = 31.4(cm)
所走路程:31.4×2 = 62.8(cm) =0.628(m)
1圈面积:S=3.14×52 = 78.5(cm2)
扫过面积:78.5×2 = 157(平方厘米)
r = 5cm
24小时 = 时针转2圈
练习4:一个钟表的分针长30厘米,从上午9点10分到9点50分,分针针尖走过的路程是多少厘米?扫过的面积是多少平方厘米?
解析:
从9点10分到9点50分,分针走了40分钟,一圈60分钟,分针走了
1圈的周长:3.14×30×2=188.4(厘米)
1圈的面积:3.14×30×30=2826(平方厘米)
半径长
04
综合巩固
综合巩固
①半径为2厘米的圆,半径增加1厘米后,它的面积增加( )
平方厘米。
解析:增加的面积即为圆环的面积。
r=2(厘米),R=2+1=3(厘米)
3.14×(32-22)=15.7(平方厘米)
15.7
②一个圆的面积为28.26平方厘米,这个圆的半径是( ) 厘米。
解析:
3
③半圆的周长为10.28厘米,它的面积为( )平方厘米。
S半圆 = 3.14 ×22÷2 = 6.28(cm2)
解析:
6.28
④如图,明星学校有一个运动场,运动场的中间是长方形,长方形的长是60米,宽是40米,两头是半圆形。求出它的周长( )米,面积( )平方米。
解析:周长 = C圆 + 50×2
面积 = S圆 + S长
60米
40米
面积:3.14×20×20 + 40×60 = 3656 (平方米)
r:40÷2 = 20 (米)
周长:3.14×40 + 60×2 = 245.6 (米)
245.6
3256
⑤一种自行车的前齿轮齿数是45,后轮齿数是15,后轮直径是60厘米,如果前轮转动两周,自行车大约前进( )米。
分析:前轮走的路程等于后轮走的路程
前轮齿数×圈数=后轮齿数×圈数
45×2 ÷ 15 = 6(周)
所以:前轮转动2周,后轮转动6周
自行车大约前进:3.14×60×6 = 1130.4cm = 11.304m
11.304
⑥直径是1.6米的圆形餐桌,高1米,上面铺了一块正方形台布,台布的四个角正好触到地面,这块台布的面积是( )平方米。
桌布对角线长度 = 1.6+1+1=3.6(米)
1.6
1
1
S正 = 对角线×对角线÷2
= 3.6×3.6÷2
= 6.48(平方米)
结论:正方形的面积 = 边长×边长 = 对角线×对角线÷2
6.48
⑦把一个圆平均分成2018个小扇形后,拼成一个近似的长方形,周长比原来增加了8厘米,求这个圆的面积是( )。
解析:拼成近似的长方形,面积不变,周长增加两条半径
r : 8÷2 = 4(厘米)
S : 3.14×42 = 50.24(平方厘米)
50.24平方厘米
⑧如图,三个相同的圆面积都是18平方厘米,求阴影部分的面积和是多少?
解析:
三个圆面积相同 三个圆的 r 相同。
∠A+∠B+∠C = 1800
可知:三个阴影部分面积之和 = 半圆的面积
S阴 = 18÷2 = 9(cm2)
⑧如图,大圆的直径是小圆直径的 倍,如果阴影部分的面积是 65 平方厘米, 那么小圆的面积是( )平方厘米。
16
⑨石头落到水中,平静水面产生的许多圆形波纹叫涟漪。
(1)设波纹以每秒 1 米的速度向四周扩散,试求 2 秒后波纹的面积?
(2)如果每秒产生一个新的波纹,并且后面的波纹以相同的速度向四周扩散。石头落到水中 3 秒后,产生的第一个波纹比第二个波纹的面积大多少平方米?
(1)分析:此时波纹形成了一个半径为2米的圆
(2)分析:根据题意求圆环的面积
THANKS
