15.4角的平分线第3课时角平分线的判定课件(共19张PPT)2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 15.4角的平分线第3课时角平分线的判定课件(共19张PPT)2024-2025学年度八年级上册沪科版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 477.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-04 13:00:08 | ||
图片预览





文档简介
(共19张PPT)
沪科版
15.4.3 角平分线的判定
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1. 探索并证明角平分线的判定:角的内部到角两边的距离相等的点在角的平分线上.
3. 会用角平分线的判定解决实际问题.
学习目标
难点
难点
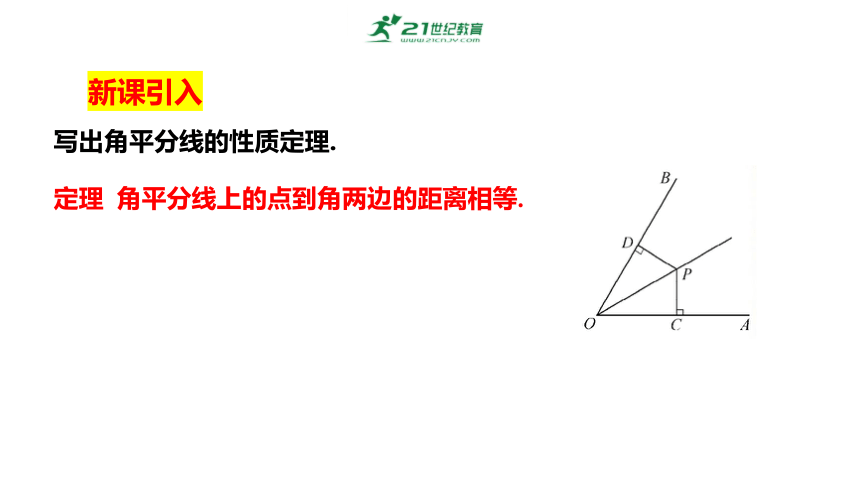
写出角平分线的性质定理.
定理 角平分线上的点到角两边的距离相等.
新课引入
写出角平分线的性质定理的逆命题.
思考
这逆命题是真命题吗?如果是真命题请写出已知、求证,并指出证明.
角的内部到角两边距离相等的点在角的平分线上.
一 角平分线的判定
新知学习
证明
如图,点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE. 求证:点P在∠AOB的平分线OC上.
O
A
B
C
P
D
E
┐
证明:∵PD⊥OA,PE⊥OB,
∴∠PEO=∠PDO=90°.
∵在Rt△PEO和Rt△PDO中,
PE=PD,
PO=PO, ∴Rt△PEO≌Rt△PDO(HL).
∴∠AOC=∠BOC. ∴点P在∠AOB的平分线OC上.
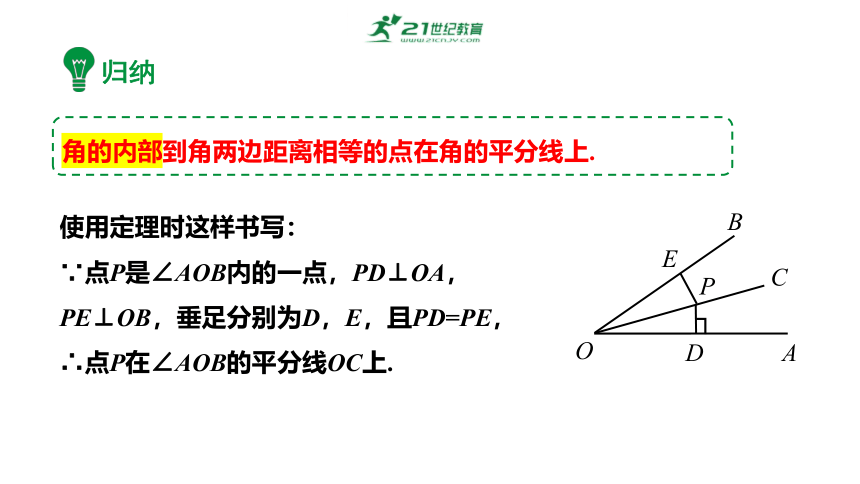
归纳
角的内部到角两边距离相等的点在角的平分线上.
使用定理时这样书写:
∵点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE,∴点P在∠AOB的平分线OC上.
O
A
B
C
P
D
E
┐
例1 如图,CD⊥AB,BE⊥AC,垂足分别为点D,E.BE,CD相交于点O,且OB=OC.求证:点O在∠BAC的平分线上.
证明:∵CD⊥AB,BE⊥AC,∴∠BDO=∠CEO=90°.
又∵OB=OC,∠BOD=∠COE,
∴△BOD≌△COE(AAS)
∴OD=OE.
∴点O在∠BAC的平分线上.
(角的内部到角两边距离相等的点在角的平分线上)
二 三角形的内角平分线
探究1
分别画出以下三角形的三个内角的角平分线,你发现了什么?
三角形的三条角平分线相交于一点,且交点位于三角形的内部.
A
B
C
┐
A
B
C
A
B
C
探究2
过交点分别作三角形三边的垂线,测量一下每一组垂线段的长度,你发现了什么?
A
B
C
A
B
B
C
A
C
过三角形三条角平分线交点作三角形三边的垂线段相等.
┐
┐
┐
┐
┐
┐
┐
┐
┐
例2 已知:如图,△ABC中,∠B的平分线BE与∠C的平分线CF相交于点P.
求证:AP平分∠BAC.
证明:过点P分别作PM⊥BC,PN⊥AC, PQ⊥ AB,垂足分别为点M,N,Q.
∵BE是∠B的平分线,点P在BE上,(已知)
∴PQ=PM.(角平分线上的点到角两边的距离相等)
同理,PN=PM.
∴PN=PQ.(等量代换)
∴AP平分∠BAC.(角的内部到角两边距离相等的点在角的平分线上)
三角形三条内角平分线相交于一点,这点到三角形三边的距离相等.
通过上面的例题可以得到什么结论?
1.到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点
B.三条高的交点
C.三条边的垂直平分线的交点
D.三条角平分线的交点
D
针对训练
随堂练习
1.如图,在△ABC 中,点 O 是△ABC 内一点,且点 O 到△ABC 三边的距离相等.若∠A=40°,则∠BOC 的度数为 ( )
A. 110° B. 120° C. 130° D. 140°
解析:由于 O 到△ABC 三边的距离相等,
故 O 是三条内角平分线的交点,
即 BO,CO 都是内角的平分线,
则∠OBC= ∠ABC,∠OCB= ∠ACB.
∵∠ABC+∠ACB=180°-∠A=180°-40°=140°,
∴∠OBC+∠OCB=70°.
∴∠BOC=180°-70°=110°.
答案:A
证明:如图,过点F作FG⊥AE于点G,FH⊥AD于点H,FM⊥BC于点M.
2.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F.
求证:点F在∠BAC的平分线上.
G
H
M
∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC.
∴FG=FM.
同理可得∴FM=FH.
∴FG=FH,
∴点F在∠BAC的平分线上.
3.如图,在直角△ABC 中,AC=BC,∠C =90°,AP 平分∠BAC,BD 平分∠ABC;AP,BD 交于点 O,过点 O 作 OM⊥AC 于点 M,若 OM=4.
(1) 求点 O 到△ABC 三边的距离和;
M
E
N
A
B
C
P
O
D
解:如图,过点 O 作 ON⊥BC 于点 N,过点 O 作 OE⊥AB 于点 E,
∵OM=4.
∴OM+ON+OE=4+4+4=12.
(2) 若△ABC 的周长为 32,求 △ABC 的面积.
解:连接 OC.
E
N
A
B
C
P
O
D
M
三角形三
条内角平
分线性质
定理 角的内部到角两边距离相等的点在角的平分线上.
三角形三条内角平分线相交于一点,这点到三角形三边
的距离相等.
角平分线
的判定
角平分线
的判定定理
课堂小结
沪科版
15.4.3 角平分线的判定
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1. 探索并证明角平分线的判定:角的内部到角两边的距离相等的点在角的平分线上.
3. 会用角平分线的判定解决实际问题.
学习目标
难点
难点
写出角平分线的性质定理.
定理 角平分线上的点到角两边的距离相等.
新课引入
写出角平分线的性质定理的逆命题.
思考
这逆命题是真命题吗?如果是真命题请写出已知、求证,并指出证明.
角的内部到角两边距离相等的点在角的平分线上.
一 角平分线的判定
新知学习
证明
如图,点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE. 求证:点P在∠AOB的平分线OC上.
O
A
B
C
P
D
E
┐
证明:∵PD⊥OA,PE⊥OB,
∴∠PEO=∠PDO=90°.
∵在Rt△PEO和Rt△PDO中,
PE=PD,
PO=PO, ∴Rt△PEO≌Rt△PDO(HL).
∴∠AOC=∠BOC. ∴点P在∠AOB的平分线OC上.
归纳
角的内部到角两边距离相等的点在角的平分线上.
使用定理时这样书写:
∵点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE,∴点P在∠AOB的平分线OC上.
O
A
B
C
P
D
E
┐
例1 如图,CD⊥AB,BE⊥AC,垂足分别为点D,E.BE,CD相交于点O,且OB=OC.求证:点O在∠BAC的平分线上.
证明:∵CD⊥AB,BE⊥AC,∴∠BDO=∠CEO=90°.
又∵OB=OC,∠BOD=∠COE,
∴△BOD≌△COE(AAS)
∴OD=OE.
∴点O在∠BAC的平分线上.
(角的内部到角两边距离相等的点在角的平分线上)
二 三角形的内角平分线
探究1
分别画出以下三角形的三个内角的角平分线,你发现了什么?
三角形的三条角平分线相交于一点,且交点位于三角形的内部.
A
B
C
┐
A
B
C
A
B
C
探究2
过交点分别作三角形三边的垂线,测量一下每一组垂线段的长度,你发现了什么?
A
B
C
A
B
B
C
A
C
过三角形三条角平分线交点作三角形三边的垂线段相等.
┐
┐
┐
┐
┐
┐
┐
┐
┐
例2 已知:如图,△ABC中,∠B的平分线BE与∠C的平分线CF相交于点P.
求证:AP平分∠BAC.
证明:过点P分别作PM⊥BC,PN⊥AC, PQ⊥ AB,垂足分别为点M,N,Q.
∵BE是∠B的平分线,点P在BE上,(已知)
∴PQ=PM.(角平分线上的点到角两边的距离相等)
同理,PN=PM.
∴PN=PQ.(等量代换)
∴AP平分∠BAC.(角的内部到角两边距离相等的点在角的平分线上)
三角形三条内角平分线相交于一点,这点到三角形三边的距离相等.
通过上面的例题可以得到什么结论?
1.到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点
B.三条高的交点
C.三条边的垂直平分线的交点
D.三条角平分线的交点
D
针对训练
随堂练习
1.如图,在△ABC 中,点 O 是△ABC 内一点,且点 O 到△ABC 三边的距离相等.若∠A=40°,则∠BOC 的度数为 ( )
A. 110° B. 120° C. 130° D. 140°
解析:由于 O 到△ABC 三边的距离相等,
故 O 是三条内角平分线的交点,
即 BO,CO 都是内角的平分线,
则∠OBC= ∠ABC,∠OCB= ∠ACB.
∵∠ABC+∠ACB=180°-∠A=180°-40°=140°,
∴∠OBC+∠OCB=70°.
∴∠BOC=180°-70°=110°.
答案:A
证明:如图,过点F作FG⊥AE于点G,FH⊥AD于点H,FM⊥BC于点M.
2.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F.
求证:点F在∠BAC的平分线上.
G
H
M
∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC.
∴FG=FM.
同理可得∴FM=FH.
∴FG=FH,
∴点F在∠BAC的平分线上.
3.如图,在直角△ABC 中,AC=BC,∠C =90°,AP 平分∠BAC,BD 平分∠ABC;AP,BD 交于点 O,过点 O 作 OM⊥AC 于点 M,若 OM=4.
(1) 求点 O 到△ABC 三边的距离和;
M
E
N
A
B
C
P
O
D
解:如图,过点 O 作 ON⊥BC 于点 N,过点 O 作 OE⊥AB 于点 E,
∵OM=4.
∴OM+ON+OE=4+4+4=12.
(2) 若△ABC 的周长为 32,求 △ABC 的面积.
解:连接 OC.
E
N
A
B
C
P
O
D
M
三角形三
条内角平
分线性质
定理 角的内部到角两边距离相等的点在角的平分线上.
三角形三条内角平分线相交于一点,这点到三角形三边
的距离相等.
角平分线
的判定
角平分线
的判定定理
课堂小结
