人教版六年级上册数学圆的周长和面积进阶课件(共25张PPT)
文档属性
| 名称 | 人教版六年级上册数学圆的周长和面积进阶课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-04 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
第十一讲:圆的周长和面积进阶
本讲聚焦
1. 方圆关系
2. 平移、旋转、割补、对称
3. 整体代入
方圆关系
PART.01
例题5:根据下面三个图形,写出圆与正方形的面积比的推到过程。(结果保留π)
①正方形内最大的圆(外切关系)
思考:圆与正方形的联系在哪里?
分析:圆的直径为正方形的边长,所以设圆的直径为2r
r
2 r
【外方内圆与外圆内方】
思考:圆与正方形的联系在哪里?
分析:圆的直径为正方形的对角线,所以设圆的直径为2r
提示:对角线互相垂直的四边形,面积都可以用对角线乘积的一半来求
2r
S正方形 = 对角线×对角线÷2
②圆内最大的正方形(内接关系)
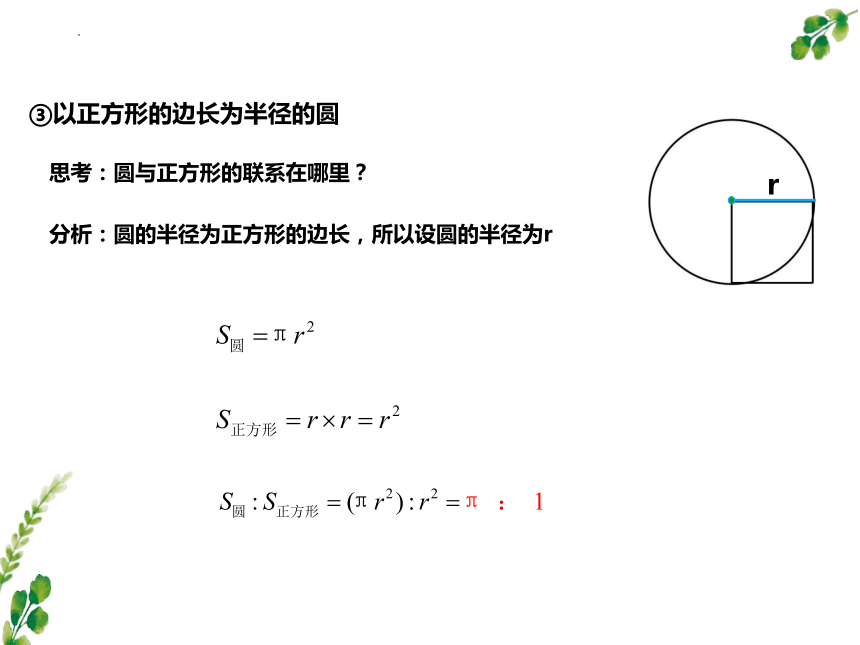
③以正方形的边长为半径的圆
思考:圆与正方形的联系在哪里?
分析:圆的半径为正方形的边长,所以设圆的半径为r
r
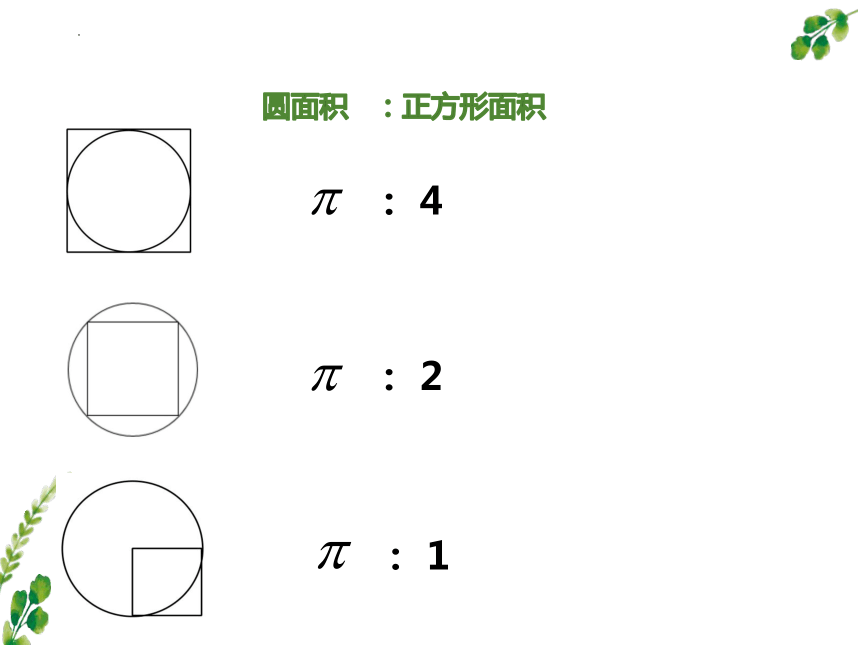
圆面积 :正方形面积
: 4
: 1
: 2
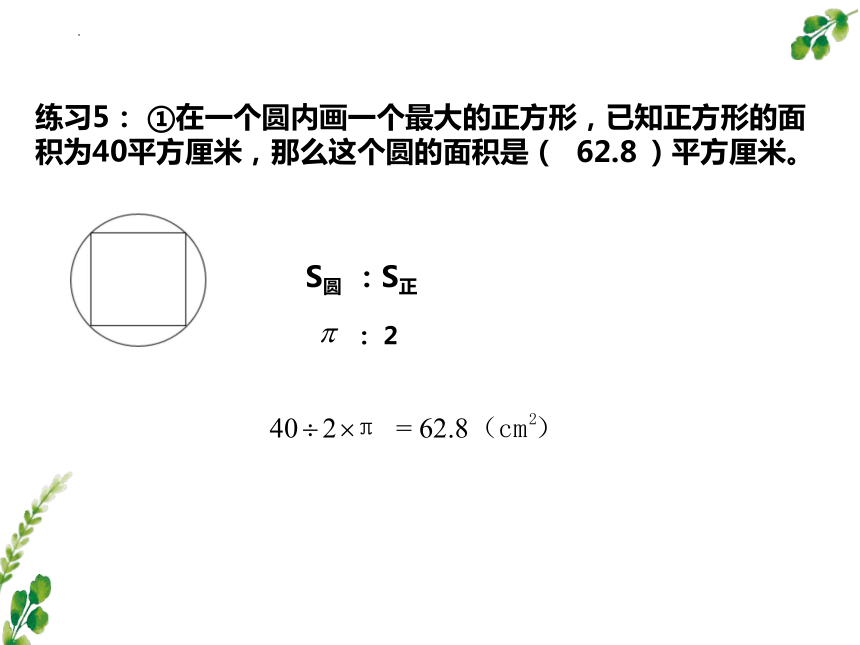
练习5: ①在一个圆内画一个最大的正方形,已知正方形的面积为40平方厘米,那么这个圆的面积是( )平方厘米。
62.8
: 2
S圆 :S正
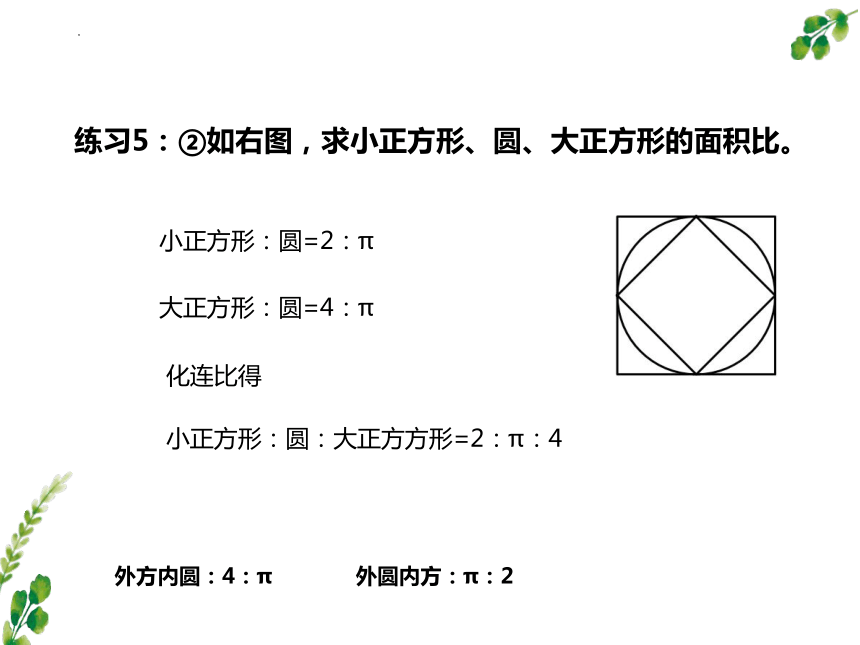
练习5:②如右图,求小正方形、圆、大正方形的面积比。
小正方形:圆=2:π
大正方形:圆=4:π
化连比得
小正方形:圆:大正方方形=2:π:4
外方内圆:4:π 外圆内方:π:2
平移、旋转、割补、对称
PART.02
例题6:计算图中阴影部分的面积(单位:厘米)
S阴 :(6+10)×6÷2=48(cm2)
S梯 = (上底+下底)×高÷2
求面积
间接法
直接法
规则图形
不规则图形 规则图形
平移、旋转、分割组合
练习6:如图,阴影部分的面积是多少?
分析:通过平移将阴影部分组合成长方形
例题7:求右图中阴影部分的面积。(π取3)
r:20÷2 = 10(cm)
S半圆:3×10×10÷2 = 150(cm2)
r:10cm
S正:10×10÷2 = 50(cm2)
S阴:150 - 50 = 100(cm2)
分析:可通过旋转平移,将两个三角形拼成一个对角线为10cm的正方形,采用整体减空白即可求出阴影部分面积。
练习7:用一张斜边为30厘米的红色直角三角形纸片,一张斜边为50厘米的蓝色直角三角形纸片,一张黄色的正方形纸片,拼成一个直角三角形;问:红、蓝两张三角形纸片的面积之和是多少?
A
B
C
D
E
E'
C'
S△:50×30÷2 = 750(cm )
50厘米
30厘米
30厘米
例题8:如图,长方形的长是8cm,则阴影部分的面积是多少平方厘米?
S阴 = (S长 - S圆×2)
÷2
8cm
r
r:8÷2÷2 = 2(cm)
4cm
宽:2×2 = 4(cm)
8×4 -
3.14×2×2×2 = 6.88 (cm2)
6.88÷2 = 3.44(cm2)
8cm
a:8÷2 = 4(cm)
a
r:4÷2 = 2(cm)
S阴 = S正 - S圆
= 4×4 - 3.14×2×2 =3.44(cm2)
法①
法②
练习8:右图中大正方形的边长是6厘米,阴影部分的面积是多少平方厘米?
6cm
S大正: 6×6 = 36(cm2)
S小正:6×6 ÷2 = 18(cm2)
(S正 = 对角线×对角线÷2)
S阴:(36 -18)÷2 = 9(cm2)
6cm
6cm
例题9:①如图所示,已知正方形的面积是10平方厘米,求圆的面积。
分析:正方形的边长等于圆的半径
S正方形=r2=10(平方厘米)
S圆=πr2=3.14×10=31.4(平方厘米)
练习9:①如图,直角三角形(直角顶点正好在圆心位置)的面积是20平方厘米,求圆的面积。
分析:直角三角形的底和高等于圆的半径
S三角形=r2÷2=20(平方厘米)
r2=20×2=40(平方厘米)
S圆=πr2=3.14×40=125.6(平方厘米)
练习9:②如图所示,阴影部分的面积是40平方米,求圆环的面积。
分析:小三角形的底和高等于小圆的半径
大三角形的底和高等于大圆的半径
令小圆半径为r,大圆半径为R,则有
R×R÷2-r×r÷2=40
(R2-r2)=80
S圆环=π(R2-r2)=3.14×80=251.2(平方米)
曲线有关的图形
1. 外方内圆:4:π 外圆内方:π:2
圆的面积;扇形的面积。(n为圆心角的度数)
圆的周长;扇形的弧长。
扇形的周长所在圆的周长直径。
3.“月牙”: 一般来说,月牙面积扇形面积-三角形面积.(除了半圆)
4.“弯角”: 弯角的面积正方形-扇形
5.“谷子”: 谷子的面积月牙面积
6.常用的思想方法:转化思想、变形、借来还去。
04
综合巩固
综合巩固
①如图,已知空白部分面积是 43dm2 。图中圆的面积是( )cm2 。
②如图,已知等腰直角三角形的直角边 AB=12cm,求阴影部分面积。(π取 3.14)
答:阴影部分的面积是20.52平方厘米。
S半圆:3.14×(12÷2)2÷2 = 56.52(cm2)
S三角形:12×(12÷2)÷2 = 36(cm2)
56.52 - 36 = 20.52(cm2)
S阴 = S半圆 - S三角形
③如图所示,在直角△ABC 中,∠C=90°,四边形 ECFD 为正方形,若 AD=36cm,DB=4cm,阴影部分的面积是( ) 。
36cm
4cm
THANKS
第十一讲:圆的周长和面积进阶
本讲聚焦
1. 方圆关系
2. 平移、旋转、割补、对称
3. 整体代入
方圆关系
PART.01
例题5:根据下面三个图形,写出圆与正方形的面积比的推到过程。(结果保留π)
①正方形内最大的圆(外切关系)
思考:圆与正方形的联系在哪里?
分析:圆的直径为正方形的边长,所以设圆的直径为2r
r
2 r
【外方内圆与外圆内方】
思考:圆与正方形的联系在哪里?
分析:圆的直径为正方形的对角线,所以设圆的直径为2r
提示:对角线互相垂直的四边形,面积都可以用对角线乘积的一半来求
2r
S正方形 = 对角线×对角线÷2
②圆内最大的正方形(内接关系)
③以正方形的边长为半径的圆
思考:圆与正方形的联系在哪里?
分析:圆的半径为正方形的边长,所以设圆的半径为r
r
圆面积 :正方形面积
: 4
: 1
: 2
练习5: ①在一个圆内画一个最大的正方形,已知正方形的面积为40平方厘米,那么这个圆的面积是( )平方厘米。
62.8
: 2
S圆 :S正
练习5:②如右图,求小正方形、圆、大正方形的面积比。
小正方形:圆=2:π
大正方形:圆=4:π
化连比得
小正方形:圆:大正方方形=2:π:4
外方内圆:4:π 外圆内方:π:2
平移、旋转、割补、对称
PART.02
例题6:计算图中阴影部分的面积(单位:厘米)
S阴 :(6+10)×6÷2=48(cm2)
S梯 = (上底+下底)×高÷2
求面积
间接法
直接法
规则图形
不规则图形 规则图形
平移、旋转、分割组合
练习6:如图,阴影部分的面积是多少?
分析:通过平移将阴影部分组合成长方形
例题7:求右图中阴影部分的面积。(π取3)
r:20÷2 = 10(cm)
S半圆:3×10×10÷2 = 150(cm2)
r:10cm
S正:10×10÷2 = 50(cm2)
S阴:150 - 50 = 100(cm2)
分析:可通过旋转平移,将两个三角形拼成一个对角线为10cm的正方形,采用整体减空白即可求出阴影部分面积。
练习7:用一张斜边为30厘米的红色直角三角形纸片,一张斜边为50厘米的蓝色直角三角形纸片,一张黄色的正方形纸片,拼成一个直角三角形;问:红、蓝两张三角形纸片的面积之和是多少?
A
B
C
D
E
E'
C'
S△:50×30÷2 = 750(cm )
50厘米
30厘米
30厘米
例题8:如图,长方形的长是8cm,则阴影部分的面积是多少平方厘米?
S阴 = (S长 - S圆×2)
÷2
8cm
r
r:8÷2÷2 = 2(cm)
4cm
宽:2×2 = 4(cm)
8×4 -
3.14×2×2×2 = 6.88 (cm2)
6.88÷2 = 3.44(cm2)
8cm
a:8÷2 = 4(cm)
a
r:4÷2 = 2(cm)
S阴 = S正 - S圆
= 4×4 - 3.14×2×2 =3.44(cm2)
法①
法②
练习8:右图中大正方形的边长是6厘米,阴影部分的面积是多少平方厘米?
6cm
S大正: 6×6 = 36(cm2)
S小正:6×6 ÷2 = 18(cm2)
(S正 = 对角线×对角线÷2)
S阴:(36 -18)÷2 = 9(cm2)
6cm
6cm
例题9:①如图所示,已知正方形的面积是10平方厘米,求圆的面积。
分析:正方形的边长等于圆的半径
S正方形=r2=10(平方厘米)
S圆=πr2=3.14×10=31.4(平方厘米)
练习9:①如图,直角三角形(直角顶点正好在圆心位置)的面积是20平方厘米,求圆的面积。
分析:直角三角形的底和高等于圆的半径
S三角形=r2÷2=20(平方厘米)
r2=20×2=40(平方厘米)
S圆=πr2=3.14×40=125.6(平方厘米)
练习9:②如图所示,阴影部分的面积是40平方米,求圆环的面积。
分析:小三角形的底和高等于小圆的半径
大三角形的底和高等于大圆的半径
令小圆半径为r,大圆半径为R,则有
R×R÷2-r×r÷2=40
(R2-r2)=80
S圆环=π(R2-r2)=3.14×80=251.2(平方米)
曲线有关的图形
1. 外方内圆:4:π 外圆内方:π:2
圆的面积;扇形的面积。(n为圆心角的度数)
圆的周长;扇形的弧长。
扇形的周长所在圆的周长直径。
3.“月牙”: 一般来说,月牙面积扇形面积-三角形面积.(除了半圆)
4.“弯角”: 弯角的面积正方形-扇形
5.“谷子”: 谷子的面积月牙面积
6.常用的思想方法:转化思想、变形、借来还去。
04
综合巩固
综合巩固
①如图,已知空白部分面积是 43dm2 。图中圆的面积是( )cm2 。
②如图,已知等腰直角三角形的直角边 AB=12cm,求阴影部分面积。(π取 3.14)
答:阴影部分的面积是20.52平方厘米。
S半圆:3.14×(12÷2)2÷2 = 56.52(cm2)
S三角形:12×(12÷2)÷2 = 36(cm2)
56.52 - 36 = 20.52(cm2)
S阴 = S半圆 - S三角形
③如图所示,在直角△ABC 中,∠C=90°,四边形 ECFD 为正方形,若 AD=36cm,DB=4cm,阴影部分的面积是( ) 。
36cm
4cm
THANKS
