人教版六年级下册数学第三单元《圆柱与圆锥》单元整体教学设计说课课件(共34张PPT)
文档属性
| 名称 | 人教版六年级下册数学第三单元《圆柱与圆锥》单元整体教学设计说课课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 19.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-04 11:12:25 | ||
图片预览






文档简介
(共34张PPT)
《圆柱与圆锥》单元教学设计
转
化
建
结
维
度
寻
促
迁
移
径
探
人教版六年级数学下册第三单元
路
构
有效的数学学习活动不能单纯的依赖模仿与记忆。动手实践,自主探索与合作交流是学生学习数学的重要方式。
一
目录
CONTENT
理论依据
教学背景
活动设计
二
三
四
五
学习目标
课时安排
六
评价设计
七
作业设计
八
教学反思
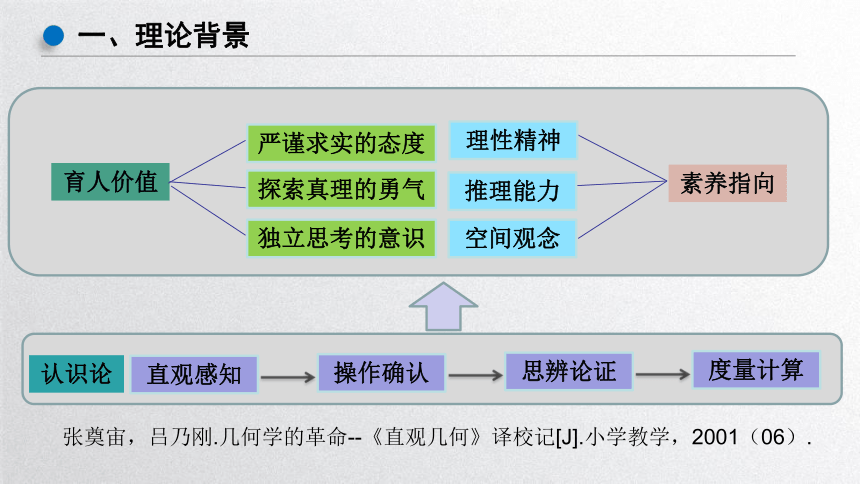
直观感知
操作确认
思辨论证
度量计算
张奠宙,吕乃刚.几何学的革命--《直观几何》译校记[J].小学教学,2001(06).
认识论
一、理论背景
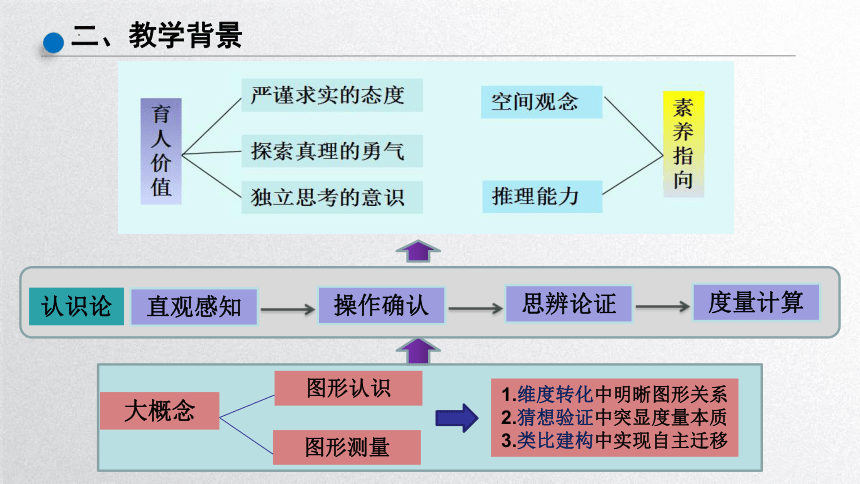
空间观念
素养指向
育人价值
理性精神
推理能力
严谨求实的态度
探索真理的勇气
独立思考的意识
一、理论背景
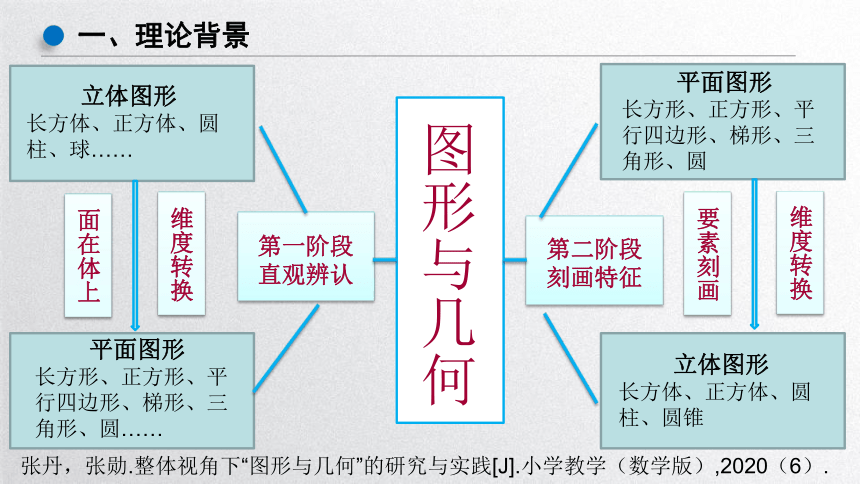
图形与几何
立体图形
长方体、正方体、圆柱、球……
平面图形
长方形、正方形、平行四边形、梯形、三角形、圆
立体图形
长方体、正方体、圆柱、圆锥
第一阶段
直观辨认
第二阶段
刻画特征
面在体上
维度转换
平面图形
长方形、正方形、平行四边形、梯形、三角形、圆……
要素刻画
维度转换
张丹,张勋.整体视角下“图形与几何”的研究与实践[J].小学教学(数学版),2020(6).
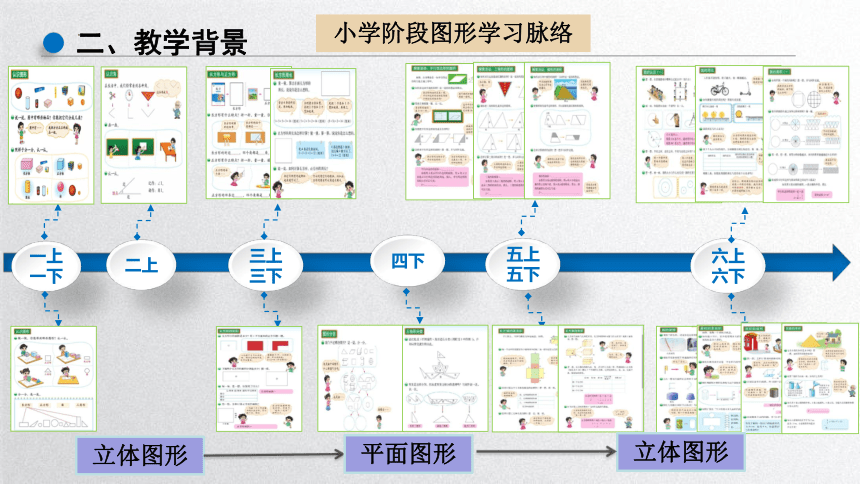
一上
一下
二、教学背景
二上
三上
三下
四下
五上
五下
六上
六下
立体图形
平面图形
立体图形
小学阶段图形学习脉络
本单元的教学内容为:
圆柱和圆锥的认识、圆柱的表面积、圆柱和圆锥的体积。
二、教学背景
本单元的学情分析:
学生已经探索并掌握了长方形、正方形和圆等一些常见的平面图形的特征,以及长方体、正方体的特征,并直观认识了圆柱与圆锥,并且已经掌握了有关“转化”的数学思想,积累了探索的经验,准备了研究的方法。为探究圆柱的侧面积、表面积以及圆柱与圆锥的体积奠定了基础。
二、教学背景
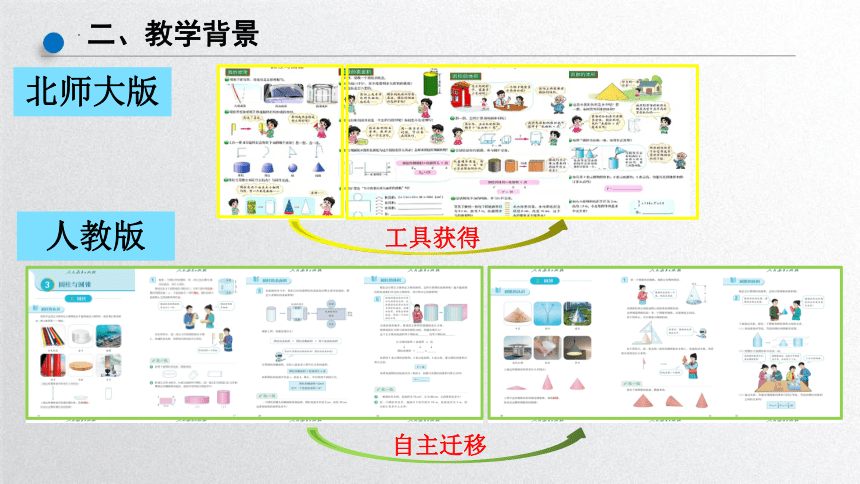
二、教学背景
北师大版
人教版
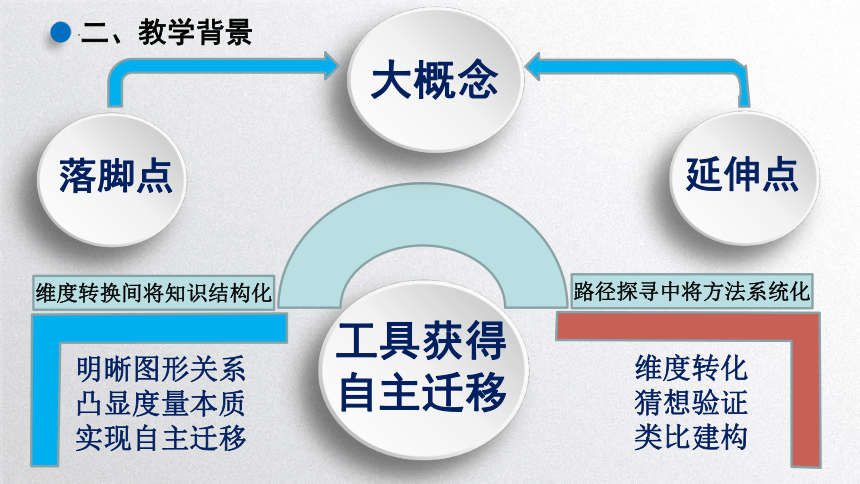
工具获得
自主迁移
二、教学背景
调研题目 调研展示 数据呈现 归因分析
人数:45人 占比:71.43%
人数:42人 占比:66.67%
人数:50人 占比:79.36%
学生头脑中还没有形成一个研究立体图形的思维路径。
缺少动手实践的活动经验去推导新图形的公式,缺少空间观念、推理意识。
工具获得
自主迁移
大概念
明晰图形关系
凸显度量本质
实现自主迁移
维度转化
猜想验证
类比建构
落脚点
延伸点
维度转换间将知识结构化
路径探寻中将方法系统化
二、教学背景
二、教学背景
1.维度转化中明晰图形关系
2.猜想验证中突显度量本质
3.类比建构中实现自主迁移
大概念
图形认识
图形测量
直观感知
操作确认
思辨论证
度量计算
认识论
三、学习目标
体会数学与生活的密切联系,感受平面图形与立体图形转化的价值,获得自主探索、发现创造、乐学善学的情感体验。
K 知能目标
认识圆柱和圆锥的基本特征和各部分名称,掌握圆柱的表面积、圆柱与圆锥的体积的计算方法,会解决与圆柱、圆锥相关的实际问题。
U 理解目标
经历展开与折叠、视图与还原、切割与堆积、旋转的过程,实现圆柱与平面图形的互相转化,在“类比猜想﹣验证”的探索过程中,获得体验与结论,形成空间观念和推理意识,积累几何活动经验。
T 迁移目标
当遇到一个新的立体图形时,有从不同角度来刻画的意识,并得到有道理的结论。
E 情感目标
三、学习目标
自觉有效使用工具研究新图形。
学习重点
理解圆柱圆锥公式的推导并能灵活应用。
学习难点
四、课时安排
圆柱与圆锥
研究内容
方法与工具
核心问题
知识技能
学习表现
旋转体的特征
表面积
体积
分类
猜想
验证
应用
如何
区分图形?
线面体互化
定性研究
定量研究
分析
表示
如何
得到图形?
如何推导
图形公式?
如何应用
图形公式?
图形要素构成与关系
二、三维之间转化关系
度量公式的获得
度量公式的应用
平移和旋转
转化和推理
研究新图形
四、课时安排
教材原有课时安排
统筹后的课时安排
图形认识 (2课时)
图形测量 (3课时)
图形应用 (4课时)
圆柱的特征
圆柱的展开图
圆锥的特征
圆柱和圆锥的认识
制作圆柱和圆锥
圆柱表面积的概念及其推导
圆柱体积公式的推导
圆锥体积公式的推导
圆柱表面积公式推导
圆柱体积公式推导
圆锥体积公式推导
圆柱表面积的实际应用
圆柱体积的实际应用
求瓶子的容积
圆锥体积的实际应用
解决问题(一)
解决问题(二)
圆柱与圆锥练习课
圆柱与圆锥复习课
五、活动设计
统筹后的课时安排
图形认识 (2课时) 圆柱和圆锥的认识
制作圆柱和圆锥
图形测量 (3课时) 圆柱表面积公式推导
圆柱体积公式推导
圆锥体积公式推导
图形应用 (4课时) 解决问题(一)
解决问题(二)
圆柱与圆锥练习课
圆柱与圆锥复习课
课程类型
关键问题
课程类型
如何
区分图形?
如何
得到图形?
如何推导
图形公式?
如何应用
图形公式?
任务1:图形分类,获得研究对象。
任务2:制定计划,获得研究方法。
任务3:动静结合研究要素及关系。
任务4:自主迁移,探索圆锥的特征。
任务5:思考得到圆柱的办法。
任务6:制作任意大小的圆柱。
任务7:制作指定大小的圆柱并探索决
定圆柱大小的要素。
任务8:探究圆锥得到的途径。
任务 9:推导圆柱的表面积公式。
任务10:猜想并验证圆柱的体积公式。
任务11:猜想并验证圆锥的体积公式。
任务12:反思研究表面积或体积的方法。
任务13:解决生活中相关实际问题。
任务14:依托图形要素进行再分类。
任务15:研究新图形的表面积或体积。
任务16:回顾反思探究图形的方法。
问题化
任务化
数学化
五、活动设计
统筹后的课时安排
图形认识 (2课时) 圆柱和圆锥的认识
制作圆柱和圆锥
课程类型
关键问题
课程类型
如何
区分图形?
任务1:图形分类,获得研究对象。
任务2:制定计划,获得研究方法。
任务3:动静结合研究要素及关系。
任务4:自主迁移,探索圆锥的特征。
课例1:《圆柱和圆锥的认识》
五、活动设计
课例1:《圆柱和圆锥的认识》
关键问题:如何区分图形?
获得研究对象
形成研究方案
明晰研究要素
实现自主迁移
任务一
图形分类
任务二
制定研究方案
任务三
动静结合探索圆柱特征
任务四
自主探索圆锥的特征
五、活动设计
课例1:《圆柱和圆锥的认识》
关键问题:如何区分图形?
“破”
“立”
构建关系
维度转换
获得要素
五、活动设计
课例2:《圆柱体积》
统筹后的课时安排
图形测量 (3课时) 圆柱表面积公式推导
圆柱体积公式推导
圆锥体积公式推导
课程类型
关键问题
课程类型
如何推导
图形公式?
任务 9:推导圆柱的表面积公式。
任务10:猜想并验证圆柱的体积公式。
任务11:猜想并验证圆锥的体积公式。
任务12:反思研究表面积或体积的方法。
五、活动设计
课例2:《圆柱体积》
关键问题:如何推导图形公式?
任务1:依托要素猜想公式
从图形走向要素
实现猜想进阶
从猜想走向验证
深化公式理解
从知识走向方法
初现路径端倪
任务2:借助经验验证公式
任务3:回顾反思概括路径
回顾我们是如何研究圆柱体积的?
五、活动设计
课例2:《圆柱体积》
关键问题:如何推导图形公式?
任务3:回顾反思概括路径
建立
联系
获得猜想
验证猜想
迁移应用
五、活动设计
统筹后的课时安排
图形应用 (4课时) 解决问题(一)
解决问题(二)
圆柱与圆锥练习课
圆柱与圆锥复习课
课程类型
关键问题
课程类型
如何应用
图形公式?
任务13:解决生活中相关实际问题。
任务14:依托图形要素进行再分类。
任务15:研究新图形的表面积或体积。
任务16:回顾反思探究图形的方法。
课例3:《圆柱和圆锥复习课》
五、活动设计
课例3:《圆柱和圆锥复习课》
关键问题:如何应用图形公式?
任务1:依托图形要素进行再分类
核心问题:
我们学过哪些立体图形?
能依据特征进行分类吗?
为什么长方体、正方体、圆柱都可以利用底面积×高计算体积?
你能从图形特征的角度分析吗?
你能用切截堆叠的工具验证吗?
实物操作
工具使用
能分类吗?
分类
标准
特征
首先找什么?
如何得到标准?
分类中寻找图形关系
辨析中加深特征理解
问题支架下,寻找共性
维度转化中,初步诠释
五、活动设计
课例3:《圆柱和圆锥复习课》
关键问题:如何应用图形公式?
任务2:操作思辨实现公式推广
V=Sh
改变底面形状
改变平移方向
长、正方形-圆-多边形-任意图形
直-倾斜-旋转
五、活动设计
课例3:《圆柱和圆锥复习课》
关键问题:如何应用图形公式?
任务3:回顾反思探究图形的方法
核心
问题
基本途径
达成目标
素养指向
如何得到公式?
有何新的想法?
直观感知
操作确认
思辨论证
度量计算
数学世界
工具获得 自主迁移
理性精神
推理能力
空间观念
育人价值
严谨求实的态度
探索真理的勇气
独立思考的意识
迁移
思维
结构
认识图形的维度
图形特征
度量公式
认知
测量
研究内容
研究方法
与要素的关系
获得公式的方法及过程
特征
表面积
体积
六、评价设计
七、作业设计
八、教学反思
在维度转化中建立知识结构凸显度量本质
在路径探寻中促进自主迁移发展核心素养
八、教学反思
1.本单元教学以“动手实践”为主线,以问题驱动数学活动,使学生在完成任务时积累几何活动经验,培养学生的空间能力、推理意识等核心素养。
2.应用几何画板的信息技术与数学学科教学相融合。有效的辅助活动突出重点、突破难点,培养学生实践能力和创新意识。
3.应用思维导图和数学日记进行整合本单元的知识,使学生构建知
识体系,实现自主迁移。
一
主
两
用
八、教学反思
严谨求实的态度
探索真理的勇气
独立思考的意识
动手实践
数学美
八、教学反思
探索怎样把过去的知识
转化成处理未来问题的有力工具
谢谢
延时符
谢 谢
《圆柱与圆锥》单元教学设计
转
化
建
结
维
度
寻
促
迁
移
径
探
人教版六年级数学下册第三单元
路
构
有效的数学学习活动不能单纯的依赖模仿与记忆。动手实践,自主探索与合作交流是学生学习数学的重要方式。
一
目录
CONTENT
理论依据
教学背景
活动设计
二
三
四
五
学习目标
课时安排
六
评价设计
七
作业设计
八
教学反思
直观感知
操作确认
思辨论证
度量计算
张奠宙,吕乃刚.几何学的革命--《直观几何》译校记[J].小学教学,2001(06).
认识论
一、理论背景
空间观念
素养指向
育人价值
理性精神
推理能力
严谨求实的态度
探索真理的勇气
独立思考的意识
一、理论背景
图形与几何
立体图形
长方体、正方体、圆柱、球……
平面图形
长方形、正方形、平行四边形、梯形、三角形、圆
立体图形
长方体、正方体、圆柱、圆锥
第一阶段
直观辨认
第二阶段
刻画特征
面在体上
维度转换
平面图形
长方形、正方形、平行四边形、梯形、三角形、圆……
要素刻画
维度转换
张丹,张勋.整体视角下“图形与几何”的研究与实践[J].小学教学(数学版),2020(6).
一上
一下
二、教学背景
二上
三上
三下
四下
五上
五下
六上
六下
立体图形
平面图形
立体图形
小学阶段图形学习脉络
本单元的教学内容为:
圆柱和圆锥的认识、圆柱的表面积、圆柱和圆锥的体积。
二、教学背景
本单元的学情分析:
学生已经探索并掌握了长方形、正方形和圆等一些常见的平面图形的特征,以及长方体、正方体的特征,并直观认识了圆柱与圆锥,并且已经掌握了有关“转化”的数学思想,积累了探索的经验,准备了研究的方法。为探究圆柱的侧面积、表面积以及圆柱与圆锥的体积奠定了基础。
二、教学背景
二、教学背景
北师大版
人教版
工具获得
自主迁移
二、教学背景
调研题目 调研展示 数据呈现 归因分析
人数:45人 占比:71.43%
人数:42人 占比:66.67%
人数:50人 占比:79.36%
学生头脑中还没有形成一个研究立体图形的思维路径。
缺少动手实践的活动经验去推导新图形的公式,缺少空间观念、推理意识。
工具获得
自主迁移
大概念
明晰图形关系
凸显度量本质
实现自主迁移
维度转化
猜想验证
类比建构
落脚点
延伸点
维度转换间将知识结构化
路径探寻中将方法系统化
二、教学背景
二、教学背景
1.维度转化中明晰图形关系
2.猜想验证中突显度量本质
3.类比建构中实现自主迁移
大概念
图形认识
图形测量
直观感知
操作确认
思辨论证
度量计算
认识论
三、学习目标
体会数学与生活的密切联系,感受平面图形与立体图形转化的价值,获得自主探索、发现创造、乐学善学的情感体验。
K 知能目标
认识圆柱和圆锥的基本特征和各部分名称,掌握圆柱的表面积、圆柱与圆锥的体积的计算方法,会解决与圆柱、圆锥相关的实际问题。
U 理解目标
经历展开与折叠、视图与还原、切割与堆积、旋转的过程,实现圆柱与平面图形的互相转化,在“类比猜想﹣验证”的探索过程中,获得体验与结论,形成空间观念和推理意识,积累几何活动经验。
T 迁移目标
当遇到一个新的立体图形时,有从不同角度来刻画的意识,并得到有道理的结论。
E 情感目标
三、学习目标
自觉有效使用工具研究新图形。
学习重点
理解圆柱圆锥公式的推导并能灵活应用。
学习难点
四、课时安排
圆柱与圆锥
研究内容
方法与工具
核心问题
知识技能
学习表现
旋转体的特征
表面积
体积
分类
猜想
验证
应用
如何
区分图形?
线面体互化
定性研究
定量研究
分析
表示
如何
得到图形?
如何推导
图形公式?
如何应用
图形公式?
图形要素构成与关系
二、三维之间转化关系
度量公式的获得
度量公式的应用
平移和旋转
转化和推理
研究新图形
四、课时安排
教材原有课时安排
统筹后的课时安排
图形认识 (2课时)
图形测量 (3课时)
图形应用 (4课时)
圆柱的特征
圆柱的展开图
圆锥的特征
圆柱和圆锥的认识
制作圆柱和圆锥
圆柱表面积的概念及其推导
圆柱体积公式的推导
圆锥体积公式的推导
圆柱表面积公式推导
圆柱体积公式推导
圆锥体积公式推导
圆柱表面积的实际应用
圆柱体积的实际应用
求瓶子的容积
圆锥体积的实际应用
解决问题(一)
解决问题(二)
圆柱与圆锥练习课
圆柱与圆锥复习课
五、活动设计
统筹后的课时安排
图形认识 (2课时) 圆柱和圆锥的认识
制作圆柱和圆锥
图形测量 (3课时) 圆柱表面积公式推导
圆柱体积公式推导
圆锥体积公式推导
图形应用 (4课时) 解决问题(一)
解决问题(二)
圆柱与圆锥练习课
圆柱与圆锥复习课
课程类型
关键问题
课程类型
如何
区分图形?
如何
得到图形?
如何推导
图形公式?
如何应用
图形公式?
任务1:图形分类,获得研究对象。
任务2:制定计划,获得研究方法。
任务3:动静结合研究要素及关系。
任务4:自主迁移,探索圆锥的特征。
任务5:思考得到圆柱的办法。
任务6:制作任意大小的圆柱。
任务7:制作指定大小的圆柱并探索决
定圆柱大小的要素。
任务8:探究圆锥得到的途径。
任务 9:推导圆柱的表面积公式。
任务10:猜想并验证圆柱的体积公式。
任务11:猜想并验证圆锥的体积公式。
任务12:反思研究表面积或体积的方法。
任务13:解决生活中相关实际问题。
任务14:依托图形要素进行再分类。
任务15:研究新图形的表面积或体积。
任务16:回顾反思探究图形的方法。
问题化
任务化
数学化
五、活动设计
统筹后的课时安排
图形认识 (2课时) 圆柱和圆锥的认识
制作圆柱和圆锥
课程类型
关键问题
课程类型
如何
区分图形?
任务1:图形分类,获得研究对象。
任务2:制定计划,获得研究方法。
任务3:动静结合研究要素及关系。
任务4:自主迁移,探索圆锥的特征。
课例1:《圆柱和圆锥的认识》
五、活动设计
课例1:《圆柱和圆锥的认识》
关键问题:如何区分图形?
获得研究对象
形成研究方案
明晰研究要素
实现自主迁移
任务一
图形分类
任务二
制定研究方案
任务三
动静结合探索圆柱特征
任务四
自主探索圆锥的特征
五、活动设计
课例1:《圆柱和圆锥的认识》
关键问题:如何区分图形?
“破”
“立”
构建关系
维度转换
获得要素
五、活动设计
课例2:《圆柱体积》
统筹后的课时安排
图形测量 (3课时) 圆柱表面积公式推导
圆柱体积公式推导
圆锥体积公式推导
课程类型
关键问题
课程类型
如何推导
图形公式?
任务 9:推导圆柱的表面积公式。
任务10:猜想并验证圆柱的体积公式。
任务11:猜想并验证圆锥的体积公式。
任务12:反思研究表面积或体积的方法。
五、活动设计
课例2:《圆柱体积》
关键问题:如何推导图形公式?
任务1:依托要素猜想公式
从图形走向要素
实现猜想进阶
从猜想走向验证
深化公式理解
从知识走向方法
初现路径端倪
任务2:借助经验验证公式
任务3:回顾反思概括路径
回顾我们是如何研究圆柱体积的?
五、活动设计
课例2:《圆柱体积》
关键问题:如何推导图形公式?
任务3:回顾反思概括路径
建立
联系
获得猜想
验证猜想
迁移应用
五、活动设计
统筹后的课时安排
图形应用 (4课时) 解决问题(一)
解决问题(二)
圆柱与圆锥练习课
圆柱与圆锥复习课
课程类型
关键问题
课程类型
如何应用
图形公式?
任务13:解决生活中相关实际问题。
任务14:依托图形要素进行再分类。
任务15:研究新图形的表面积或体积。
任务16:回顾反思探究图形的方法。
课例3:《圆柱和圆锥复习课》
五、活动设计
课例3:《圆柱和圆锥复习课》
关键问题:如何应用图形公式?
任务1:依托图形要素进行再分类
核心问题:
我们学过哪些立体图形?
能依据特征进行分类吗?
为什么长方体、正方体、圆柱都可以利用底面积×高计算体积?
你能从图形特征的角度分析吗?
你能用切截堆叠的工具验证吗?
实物操作
工具使用
能分类吗?
分类
标准
特征
首先找什么?
如何得到标准?
分类中寻找图形关系
辨析中加深特征理解
问题支架下,寻找共性
维度转化中,初步诠释
五、活动设计
课例3:《圆柱和圆锥复习课》
关键问题:如何应用图形公式?
任务2:操作思辨实现公式推广
V=Sh
改变底面形状
改变平移方向
长、正方形-圆-多边形-任意图形
直-倾斜-旋转
五、活动设计
课例3:《圆柱和圆锥复习课》
关键问题:如何应用图形公式?
任务3:回顾反思探究图形的方法
核心
问题
基本途径
达成目标
素养指向
如何得到公式?
有何新的想法?
直观感知
操作确认
思辨论证
度量计算
数学世界
工具获得 自主迁移
理性精神
推理能力
空间观念
育人价值
严谨求实的态度
探索真理的勇气
独立思考的意识
迁移
思维
结构
认识图形的维度
图形特征
度量公式
认知
测量
研究内容
研究方法
与要素的关系
获得公式的方法及过程
特征
表面积
体积
六、评价设计
七、作业设计
八、教学反思
在维度转化中建立知识结构凸显度量本质
在路径探寻中促进自主迁移发展核心素养
八、教学反思
1.本单元教学以“动手实践”为主线,以问题驱动数学活动,使学生在完成任务时积累几何活动经验,培养学生的空间能力、推理意识等核心素养。
2.应用几何画板的信息技术与数学学科教学相融合。有效的辅助活动突出重点、突破难点,培养学生实践能力和创新意识。
3.应用思维导图和数学日记进行整合本单元的知识,使学生构建知
识体系,实现自主迁移。
一
主
两
用
八、教学反思
严谨求实的态度
探索真理的勇气
独立思考的意识
动手实践
数学美
八、教学反思
探索怎样把过去的知识
转化成处理未来问题的有力工具
谢谢
延时符
谢 谢
