2024-2025学年北师大版八年级数学上册课件1.1 探索勾股定理(第2课时) 勾股定理的验证及应用课件(26张PPT)
文档属性
| 名称 | 2024-2025学年北师大版八年级数学上册课件1.1 探索勾股定理(第2课时) 勾股定理的验证及应用课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-04 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
北师大版八年级数学上册课件
第一章 勾股定理
1.1 探索勾股定理
第2课时 勾股定理的验证及应用
1.探索勾股定理
2.掌握勾股定理的内容,会用面积法验证勾股定理.
3.能运用勾股定理解决一些简单的实际问题.
探究新知
图中是四个全等的直角三角形,两直角边分别为a和b,斜边为c.请你开动脑筋,用它们拼出一个正方形.
有不同的拼法吗?
a
a
a
a
b
b
b
b
c
c
c
c
方法小结:我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
大正方形的面积可以表示为________;
也可以表示为___________.
(a+b)2
c2 +4·ab/2
∵ (a+b)2 = c2 + 4·ab/2
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
验证方法:毕达哥拉斯证法
做一做
在纸上画一个直角三角形,分别以这个直角三角形的三边为边长向外作正方形。
b
a
c
图1-4
为了方便计算图中大正方形的面积,
对其进行适当割补:
S正方形ABCD= c2+2ab=(a+b)2
c2=a2+b2
图1-5
b
a
c
A
B
C
D
S正方形ABCD= c2-2ab=(b-a)2
c2=a2+b2
图1-6
b
a
c
A
B
C
D
【归纳】勾股定理的证明方法有300多种,必须是直角三角形的三边才能满足a2+b2=c2.
a
b
c
A
B
C
D
E
F
O
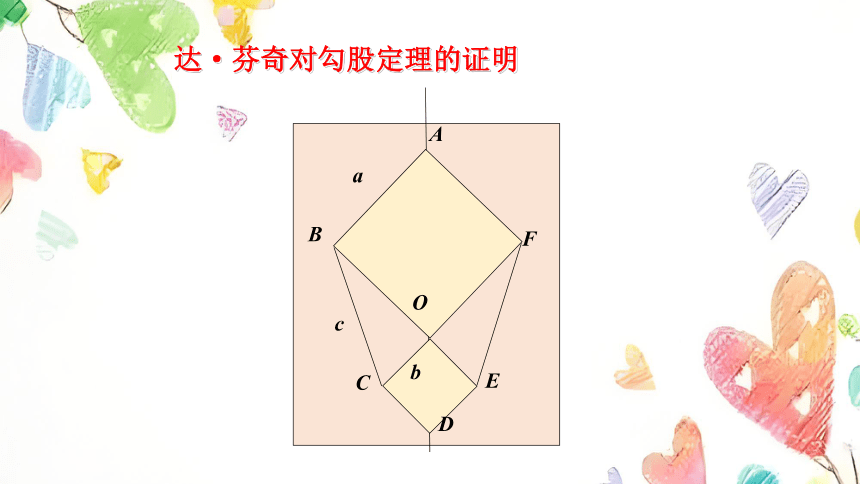
达·芬奇对勾股定理的证明
课堂小结
探索勾股定理
勾股定理的验证
勾股定理的简单运用
例1 以图甲中的直角三角形为基础,可以构造出以 , 为底,以 为高的直角梯形(如图乙).请你利用图乙验证勾股定理.
【点拨】用拼图法证明勾股定理的基本思路是:通过割补、拼接得到不同(或同一个)图形,借助面积不变的原理,得出面积之间的关系,通过代数恒等变形即可验证勾股定理.
名师点拨
【解】因为 ,
所以 .
又因为 ,
所以 .所以 .
因为 ,
所以 .
整理得 .
变式 勾股定理神秘而美妙,它的证法多样,“面积法”是常用的方法之一.当两个全等的直角三角形( 与 )按如图所示方式摆放时,请你验证勾股定理.(其中 )
解:如图,连接 ,过点 作 边上的高 ,则 .
因为 ,
,
所以 .
所以 .
例2 如图,在铁路 附近有两个村庄 , ,它们到铁路的距离分别是 和 ,作 , ,垂足分别为 , ,且 .现要在铁路旁建一个农副产品收购站 ,使 站到 , 两村的距离相等.你知道应该把 站建在距点 多远的地方吗?
【点拨】设 ,由垂直关系可以想到用勾股定理,根据 建立方程,即可使问题得解.
【解】因为 ,
所以 .
设 ,
则 ,
解得 .
答:应把 站建在距点 远的地方.
易错示例 在 中, , , 边上的高 ,则 的周长为__________.
【错解】
或
【点拨】 边上的高 可能在 的内部,也可能在 的外部,错解只考虑了一种情况.
1. 下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
D
2. 如图,这是用 个全等的直角三角形与 个小正方形镶嵌而成的正方形图案.已知大正方形的面积为 ,小正方形的面积为 .若用 , 表示直角三角形的两直角边长,有下列结论:① ;② ;③ .其中正确的结论是( )
A. ①② B. ② C. ①②③ D. ①③
C
(第2题图)
3. 如图,一轮船以 海里 时的速度从港口 出发向东北方向航行,另一轮船以 海里 时的速度同时从港口 出发向东南方向航行,则 小时后,两船相距( )
A. 海里 B. 海里
C. 海里 D. 海里
D
(第3题图)
4. 有一只喜鹊在一棵 高的小树上觅食,它的巢筑在距离该树 的一棵大树上,大树高 ,且巢离树顶部 .当它听到巢中幼鸟的叫声时,立即赶过去.如果它飞行的速度为 ,那么它至少需要多少时间才能赶回巢中?
解:如图,
由题意知 , , .
过点 作 于点 ,则 , .
在 中,
.
所以 , .
5. 如图,数学活动课上,老师组织学生测量学校旗杆的高度.同学们发现系在旗杆顶端的绳子拉直垂到了地面且还多 .同学们把绳子的末端拉开 后,发现绳子末端刚好接触地面,求旗杆的高度.(旗杆顶端滑轮上方的部分忽略不计)
解:设旗杆 的高度为 ,则绳子 的长度为 .
在 中,根据勾股定理可得
.
解得 .
答:旗杆的高度为 .
6. 如图,教学楼走廊左右两侧是竖直的墙,一架梯子 斜靠在左墙时,梯子底端 到左墙角 的距离为 ,顶端 距离地面 .如果保持梯子底端 的位置不动,将梯子斜靠在右墙,此时顶端 距离地面 ,求教学楼走廊的宽度 .
解:在 中,
因为 , , ,
所以 .
在 中,因为 , , ,
所以 .
所以 .
解得 .
所以 .
答:教学楼走廊的宽度是 .
完成学生书对应课时练习
作业布置
谢谢观看
北师大版八年级数学上册课件
第一章 勾股定理
1.1 探索勾股定理
第2课时 勾股定理的验证及应用
1.探索勾股定理
2.掌握勾股定理的内容,会用面积法验证勾股定理.
3.能运用勾股定理解决一些简单的实际问题.
探究新知
图中是四个全等的直角三角形,两直角边分别为a和b,斜边为c.请你开动脑筋,用它们拼出一个正方形.
有不同的拼法吗?
a
a
a
a
b
b
b
b
c
c
c
c
方法小结:我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
大正方形的面积可以表示为________;
也可以表示为___________.
(a+b)2
c2 +4·ab/2
∵ (a+b)2 = c2 + 4·ab/2
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
验证方法:毕达哥拉斯证法
做一做
在纸上画一个直角三角形,分别以这个直角三角形的三边为边长向外作正方形。
b
a
c
图1-4
为了方便计算图中大正方形的面积,
对其进行适当割补:
S正方形ABCD= c2+2ab=(a+b)2
c2=a2+b2
图1-5
b
a
c
A
B
C
D
S正方形ABCD= c2-2ab=(b-a)2
c2=a2+b2
图1-6
b
a
c
A
B
C
D
【归纳】勾股定理的证明方法有300多种,必须是直角三角形的三边才能满足a2+b2=c2.
a
b
c
A
B
C
D
E
F
O
达·芬奇对勾股定理的证明
课堂小结
探索勾股定理
勾股定理的验证
勾股定理的简单运用
例1 以图甲中的直角三角形为基础,可以构造出以 , 为底,以 为高的直角梯形(如图乙).请你利用图乙验证勾股定理.
【点拨】用拼图法证明勾股定理的基本思路是:通过割补、拼接得到不同(或同一个)图形,借助面积不变的原理,得出面积之间的关系,通过代数恒等变形即可验证勾股定理.
名师点拨
【解】因为 ,
所以 .
又因为 ,
所以 .所以 .
因为 ,
所以 .
整理得 .
变式 勾股定理神秘而美妙,它的证法多样,“面积法”是常用的方法之一.当两个全等的直角三角形( 与 )按如图所示方式摆放时,请你验证勾股定理.(其中 )
解:如图,连接 ,过点 作 边上的高 ,则 .
因为 ,
,
所以 .
所以 .
例2 如图,在铁路 附近有两个村庄 , ,它们到铁路的距离分别是 和 ,作 , ,垂足分别为 , ,且 .现要在铁路旁建一个农副产品收购站 ,使 站到 , 两村的距离相等.你知道应该把 站建在距点 多远的地方吗?
【点拨】设 ,由垂直关系可以想到用勾股定理,根据 建立方程,即可使问题得解.
【解】因为 ,
所以 .
设 ,
则 ,
解得 .
答:应把 站建在距点 远的地方.
易错示例 在 中, , , 边上的高 ,则 的周长为__________.
【错解】
或
【点拨】 边上的高 可能在 的内部,也可能在 的外部,错解只考虑了一种情况.
1. 下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
D
2. 如图,这是用 个全等的直角三角形与 个小正方形镶嵌而成的正方形图案.已知大正方形的面积为 ,小正方形的面积为 .若用 , 表示直角三角形的两直角边长,有下列结论:① ;② ;③ .其中正确的结论是( )
A. ①② B. ② C. ①②③ D. ①③
C
(第2题图)
3. 如图,一轮船以 海里 时的速度从港口 出发向东北方向航行,另一轮船以 海里 时的速度同时从港口 出发向东南方向航行,则 小时后,两船相距( )
A. 海里 B. 海里
C. 海里 D. 海里
D
(第3题图)
4. 有一只喜鹊在一棵 高的小树上觅食,它的巢筑在距离该树 的一棵大树上,大树高 ,且巢离树顶部 .当它听到巢中幼鸟的叫声时,立即赶过去.如果它飞行的速度为 ,那么它至少需要多少时间才能赶回巢中?
解:如图,
由题意知 , , .
过点 作 于点 ,则 , .
在 中,
.
所以 , .
5. 如图,数学活动课上,老师组织学生测量学校旗杆的高度.同学们发现系在旗杆顶端的绳子拉直垂到了地面且还多 .同学们把绳子的末端拉开 后,发现绳子末端刚好接触地面,求旗杆的高度.(旗杆顶端滑轮上方的部分忽略不计)
解:设旗杆 的高度为 ,则绳子 的长度为 .
在 中,根据勾股定理可得
.
解得 .
答:旗杆的高度为 .
6. 如图,教学楼走廊左右两侧是竖直的墙,一架梯子 斜靠在左墙时,梯子底端 到左墙角 的距离为 ,顶端 距离地面 .如果保持梯子底端 的位置不动,将梯子斜靠在右墙,此时顶端 距离地面 ,求教学楼走廊的宽度 .
解:在 中,
因为 , , ,
所以 .
在 中,因为 , , ,
所以 .
所以 .
解得 .
所以 .
答:教学楼走廊的宽度是 .
完成学生书对应课时练习
作业布置
谢谢观看
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
