湖南省岳阳市第一中学2015-2016学年高一上学期期中考试数学试题
文档属性
| 名称 | 湖南省岳阳市第一中学2015-2016学年高一上学期期中考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 163.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-21 21:53:34 | ||
图片预览



文档简介
岳阳市一中2015年高一期中考试
数学试题
满分:100分 时量:120分钟 命题:刘江波
一、选择题:本大题共12小题,每小题3分,共计36分,在每小题给出的四个选项中,只有一项符合题目要求,请把正确答案的代号填在答题卡上.
1.已知集合A={4,5,7,9},B={3,4,7,8,9},全集U=A∪B,
则集合CU(A∩B)=( )
A、 B、 C、 D、
2.将梯形沿某一方向平移形成的几何体是( )
A.四棱柱 B.四棱锥
C.四棱台 D.圆台
3.若集合的子集个数为2个,则实数的值为 ( ).
A.0或1 B.0 C.1 D.0或
4.下列各组函数中表示同一函数的是( )
①f(x)=与g(x)=x; ②f(x)=|x|与g(x)=;
③f(x)=x0与g(x)=; ④f(x)=x2-2x-1与g(t)=t2-2t-1.
A.①② B.②③ C.③④ D.①④
5.下列各函数在其定义域中,既是奇函数,又是增函数的是( )
A.y=x+1 B.y=-x3 C. D.y=x|x|
6.设函数f定义如下表,一列数x0,x1,x2,x3……满足x0=5,且对任意自然数均有
xn+1=f(xn),则x2015的值为( )
x 1 2 3 4 5
f(x) 4 1 3 5 2
A.1 B.2 C.4 D.5
7.若集合,则( )
A. B. C. D.
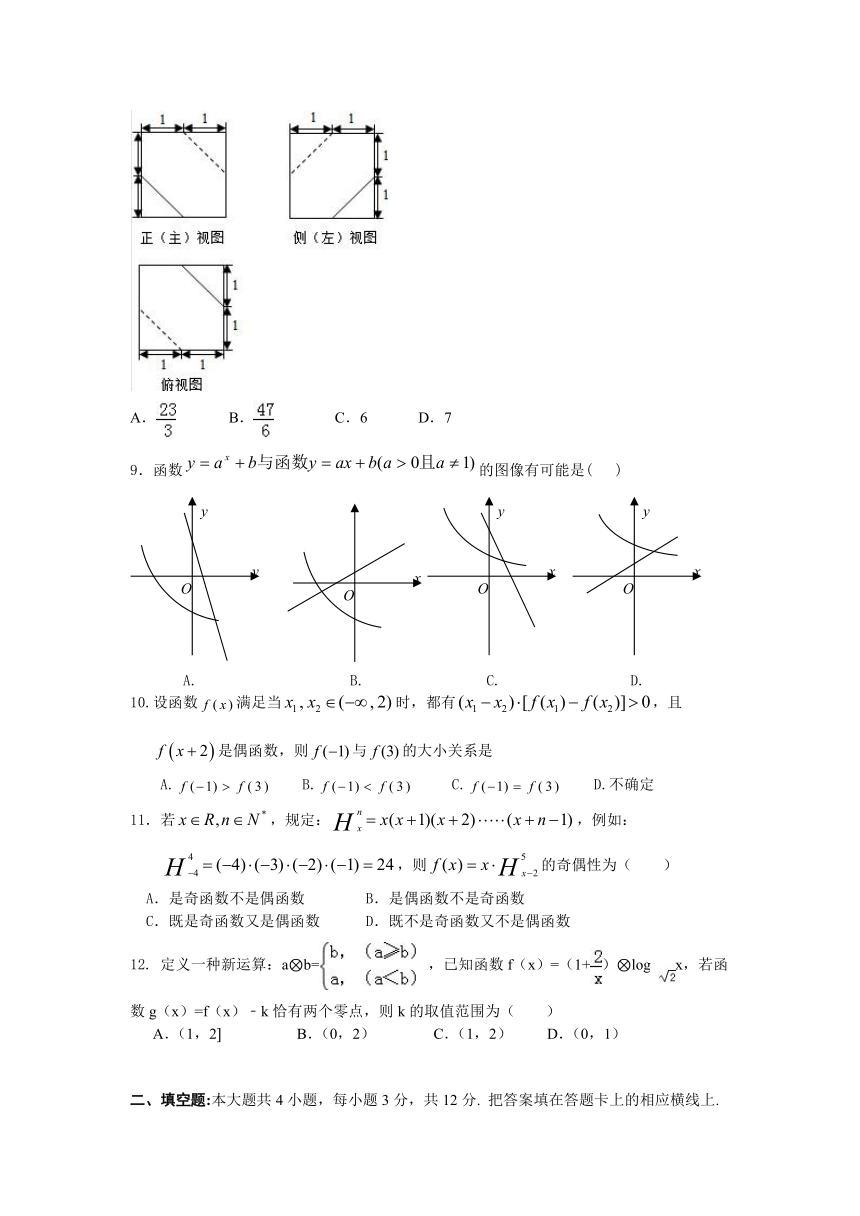
8.一个多面体的三视图如图所示,则该多面体的体积为( )
( http: / / www.21cnjy.com )
A. B. C.6 D.7
9.函数的图像有可能是( )
A. B. C. D.
10.设函数满足当时,都有,且
是偶函数,则与的大小关系是
A. B. C. D.不确定
11.若,规定:,例如:
,则的奇偶性为( )
A.是奇函数不是偶函数 B.是偶函数不是奇函数
C.既是奇函数又是偶函数 D.既不是奇函数又不是偶函数
12. 定义一种新运算:a b=,已知函数f(x)=(1+) logx,若函数g(x)=f(x)﹣k恰有两个零点,则k的取值范围为( )
A.(1,2] B.(0,2) C.(1,2) D.(0,1)
二、填空题:本大题共4小题,每小题3分,共12分. 把答案填在答题卡上的相应横线上.
13. 已知,那么、、的大小关系为 .
(用 号表示)。
13. 已知幂函数f(x)的图象过点(2,),则= .
14.在二分法求方程的一个近似根时,现在已经将根锁定在(1,2)内,则下一步可以断定根所在区间为_____________。
16. 给出下列四个命题:
(1)函数的图象过定点(1,0);
(2)已知函数是定义在上的偶函数,当时,,
则的解析式为;
(3)若,则的取值范围是;
(4)若 (,),则.
其中所有正确命题的序号是 .
三、解答题:本大题共6小题,共52分. 解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分6分)
已知
求的取值范围。
18. (本小题满8分)
已知某几何体的俯视图是如图所示矩形.主视图是一个底边长为8、高为4的等腰三角形,左视图是一个底边长为6、高为4的等腰三角形.
(1)判断该几何体形状;
(2)求该几何体的的体积V与侧面积S.
19.(本小题满分8分)
已知函数f(x)=|x﹣1|+|x+1|(x∈R)
将函数解析式写成分段函数的形式,
然后画出函数图象,并写出函数的值域;
(2)利用图象写出不等式f(x)>x+2的解集.
20.(本小题满分10分)
通过研究学生的行为,心理学家发现,学生的接受能力依赖于教师引入概念和描述问题所用的时间. 讲座开始时,学生的兴趣急增;中间有一段不太长的时间,学生的学习兴趣保持较理想的状态,随后学生的学习兴趣开始分散. 分析结果和实验表明,用表示学生掌握和接受概念的能力,x表示提出和讲授概念的时间(单位分)可以用下面公式:
(1)开讲后多少分钟,学生的接受能力最强?能持续多长时间?
(2)一个数学难题,需要55的接受能力以及13分钟时间,教师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
21.(本小题满分10分)
已知二次函数f(x)=ax2+bx(a,b为常数,且a≠0)满足条件:f(x﹣1)=f(3﹣x),且方程f(x)=2x有两等根.
(1)求f(x)的解析式.
(2)求f(x)在[0,t]上的最大值.
(3)是否存在实数m、n(m<n),使f(x)的定义域和值域分别为[m,n]和[4m,4n],
如果存在,求出m、n的值,如果不存在,说明理由.
22.(本小题满分10分)
设f(x)=为奇函数,a为常数.
(1) 求a的值;
(2) 判断f(x)在区间(1,+∞)上的单调性,并证明你的结论;
(3)若对于区间(3,4)上的每一个x的值,不等式f(x)>恒成立,
求实数m的取值范围.
高一数学参考答案
一、选择题:
1.【C】 2.【A】 3. 【A】 4. 【C】
5.【D】 6.【C】 7.【B】 8.【A】
9.【D】 10.【B】 11.【B】 12.【C】
二、填空题
13. 14. 3
15.(1.5,2) 16. (2)(3)(4)
三、解答题
17.解:,此时符合题意;(2分)
( http: / / www.21cnjy.com ),此时亦符合题意。(3分)
(1分)
18.解:(1)由已知可得该几何体是一个底面为矩形,高为4,顶点在底面的射影是矩形中心的四棱锥.(这个几何体是四棱锥,可给分).……2分
(2)作出该几何体的直观图,如图,E、F为AB、BC的中点,
则AB=8, BC=6, PO=4.
V=×(8×6)×4=64. ……2分
在Rt△POF中,PF==4,
∴S△PBC=×6×4=12,
在Rt△POE中,PE==5,
∴S△PAB=×8×5=20,
所以侧面积为2(12+20)=24+40. ……4分
19.解: (1) 原函数式可化为:
( http: / / www.21cnjy.com );……2分
其图象如右图所示,……2分
由函数图象知,函数的值域为[2,+∞)…… 1分
(2)由函数图象知,
当x=0或2时,f(x)=x+2.
结合图象可得,不等式的解集为{x|x<0或x>2} ……3分
20.解: (1)当时,=,
故其递增,最大值为,
显然在上,递减,,
因此开讲后10分钟达到最强的接受状态,并维持6分钟. ……5分
(2)当时,令,得;
当时,令,得;因此学生达到55的接受能力的时间为,教师来不及在学生达到最佳接受状态时就结束讲授. ……5分
21.解:(1)∵方程f(x)=2x有两等根,ax2+(b﹣2)x=0有两等根,
∴△=(b﹣2)2=0,解得b=2,
∵f(x﹣1)=f(3﹣x),∴x=1是函数的对称轴,
又此函数图象的对称轴是直线x=﹣,∴﹣=1,∴a=﹣1,
故f(x)=﹣x2+2x;……3分
(2)∵函数f(x)=﹣x2+2x对称轴为x=1,x∈[0,t],
∴当t≤1时,f(x)在[0,t]上是增函数,∴f(x)max=﹣t2+2t,
当t>1时,f(x)在[0,1]上是增函数,在[1,t]上是减函数,∴f(a)max=f(1)=1,
综上,.……3分
(3)∵f(x)=﹣(x﹣1)2+1≤1,∴4n≤1,即n≤.
而抛物线y=﹣x2+2x的对称轴为x=1,∴当n≤时,f(x)在[m,n]上为增函数.
若满足题设条件的m,n存在,则
即 又m<n≤.
∴m=﹣2,n=0,这时,定义域为[﹣2,0],值域为[﹣8,0].
由以上知满足条件的m,n存在,m=﹣2,n=0.……4分
22.解:(1)∵f(x)是奇函数,∴定义域关于原点对称,
由,得(x﹣1)(1﹣ax)>0.
令(x﹣1)(1﹣ax)=0,得x1=1,x2=,∴=﹣1,解得a=﹣1.……3分
(2)令u(x)==1+,设任意x1<x2,且x1, x2∈(1,+∞),
则u(x1)﹣u(x2)=,
∵1<x1<x2,∴x1﹣1>0,x2﹣1>0,x2﹣x1>0,
∴u(x1)﹣u(x2)>0,即u(x1)>u(x2).
∴u(x)=1+(x>1)是减函数,
又为减函数,
∴f(x)=在(1,+∞)上为增函数.……4分
(3)由题意知﹣>m,x∈(3,4)时恒成立,
令g(x)=﹣,x∈(3,4),由(1)知在[3,4]上为增函数,又﹣在(3,4)上也是增函数,
故g(x)在(3,4)上为增函数,
∴g(x)的最小值为g(3)=﹣=﹣,
∴m≤﹣,故实数m的范围是(﹣∞,﹣].……3分
y
x
y
x
O
x
O
x
y
O
x
y
O
数学试题
满分:100分 时量:120分钟 命题:刘江波
一、选择题:本大题共12小题,每小题3分,共计36分,在每小题给出的四个选项中,只有一项符合题目要求,请把正确答案的代号填在答题卡上.
1.已知集合A={4,5,7,9},B={3,4,7,8,9},全集U=A∪B,
则集合CU(A∩B)=( )
A、 B、 C、 D、
2.将梯形沿某一方向平移形成的几何体是( )
A.四棱柱 B.四棱锥
C.四棱台 D.圆台
3.若集合的子集个数为2个,则实数的值为 ( ).
A.0或1 B.0 C.1 D.0或
4.下列各组函数中表示同一函数的是( )
①f(x)=与g(x)=x; ②f(x)=|x|与g(x)=;
③f(x)=x0与g(x)=; ④f(x)=x2-2x-1与g(t)=t2-2t-1.
A.①② B.②③ C.③④ D.①④
5.下列各函数在其定义域中,既是奇函数,又是增函数的是( )
A.y=x+1 B.y=-x3 C. D.y=x|x|
6.设函数f定义如下表,一列数x0,x1,x2,x3……满足x0=5,且对任意自然数均有
xn+1=f(xn),则x2015的值为( )
x 1 2 3 4 5
f(x) 4 1 3 5 2
A.1 B.2 C.4 D.5
7.若集合,则( )
A. B. C. D.
8.一个多面体的三视图如图所示,则该多面体的体积为( )
( http: / / www.21cnjy.com )
A. B. C.6 D.7
9.函数的图像有可能是( )
A. B. C. D.
10.设函数满足当时,都有,且
是偶函数,则与的大小关系是
A. B. C. D.不确定
11.若,规定:,例如:
,则的奇偶性为( )
A.是奇函数不是偶函数 B.是偶函数不是奇函数
C.既是奇函数又是偶函数 D.既不是奇函数又不是偶函数
12. 定义一种新运算:a b=,已知函数f(x)=(1+) logx,若函数g(x)=f(x)﹣k恰有两个零点,则k的取值范围为( )
A.(1,2] B.(0,2) C.(1,2) D.(0,1)
二、填空题:本大题共4小题,每小题3分,共12分. 把答案填在答题卡上的相应横线上.
13. 已知,那么、、的大小关系为 .
(用 号表示)。
13. 已知幂函数f(x)的图象过点(2,),则= .
14.在二分法求方程的一个近似根时,现在已经将根锁定在(1,2)内,则下一步可以断定根所在区间为_____________。
16. 给出下列四个命题:
(1)函数的图象过定点(1,0);
(2)已知函数是定义在上的偶函数,当时,,
则的解析式为;
(3)若,则的取值范围是;
(4)若 (,),则.
其中所有正确命题的序号是 .
三、解答题:本大题共6小题,共52分. 解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分6分)
已知
求的取值范围。
18. (本小题满8分)
已知某几何体的俯视图是如图所示矩形.主视图是一个底边长为8、高为4的等腰三角形,左视图是一个底边长为6、高为4的等腰三角形.
(1)判断该几何体形状;
(2)求该几何体的的体积V与侧面积S.
19.(本小题满分8分)
已知函数f(x)=|x﹣1|+|x+1|(x∈R)
将函数解析式写成分段函数的形式,
然后画出函数图象,并写出函数的值域;
(2)利用图象写出不等式f(x)>x+2的解集.
20.(本小题满分10分)
通过研究学生的行为,心理学家发现,学生的接受能力依赖于教师引入概念和描述问题所用的时间. 讲座开始时,学生的兴趣急增;中间有一段不太长的时间,学生的学习兴趣保持较理想的状态,随后学生的学习兴趣开始分散. 分析结果和实验表明,用表示学生掌握和接受概念的能力,x表示提出和讲授概念的时间(单位分)可以用下面公式:
(1)开讲后多少分钟,学生的接受能力最强?能持续多长时间?
(2)一个数学难题,需要55的接受能力以及13分钟时间,教师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
21.(本小题满分10分)
已知二次函数f(x)=ax2+bx(a,b为常数,且a≠0)满足条件:f(x﹣1)=f(3﹣x),且方程f(x)=2x有两等根.
(1)求f(x)的解析式.
(2)求f(x)在[0,t]上的最大值.
(3)是否存在实数m、n(m<n),使f(x)的定义域和值域分别为[m,n]和[4m,4n],
如果存在,求出m、n的值,如果不存在,说明理由.
22.(本小题满分10分)
设f(x)=为奇函数,a为常数.
(1) 求a的值;
(2) 判断f(x)在区间(1,+∞)上的单调性,并证明你的结论;
(3)若对于区间(3,4)上的每一个x的值,不等式f(x)>恒成立,
求实数m的取值范围.
高一数学参考答案
一、选择题:
1.【C】 2.【A】 3. 【A】 4. 【C】
5.【D】 6.【C】 7.【B】 8.【A】
9.【D】 10.【B】 11.【B】 12.【C】
二、填空题
13. 14. 3
15.(1.5,2) 16. (2)(3)(4)
三、解答题
17.解:,此时符合题意;(2分)
( http: / / www.21cnjy.com ),此时亦符合题意。(3分)
(1分)
18.解:(1)由已知可得该几何体是一个底面为矩形,高为4,顶点在底面的射影是矩形中心的四棱锥.(这个几何体是四棱锥,可给分).……2分
(2)作出该几何体的直观图,如图,E、F为AB、BC的中点,
则AB=8, BC=6, PO=4.
V=×(8×6)×4=64. ……2分
在Rt△POF中,PF==4,
∴S△PBC=×6×4=12,
在Rt△POE中,PE==5,
∴S△PAB=×8×5=20,
所以侧面积为2(12+20)=24+40. ……4分
19.解: (1) 原函数式可化为:
( http: / / www.21cnjy.com );……2分
其图象如右图所示,……2分
由函数图象知,函数的值域为[2,+∞)…… 1分
(2)由函数图象知,
当x=0或2时,f(x)=x+2.
结合图象可得,不等式的解集为{x|x<0或x>2} ……3分
20.解: (1)当时,=,
故其递增,最大值为,
显然在上,递减,,
因此开讲后10分钟达到最强的接受状态,并维持6分钟. ……5分
(2)当时,令,得;
当时,令,得;因此学生达到55的接受能力的时间为,教师来不及在学生达到最佳接受状态时就结束讲授. ……5分
21.解:(1)∵方程f(x)=2x有两等根,ax2+(b﹣2)x=0有两等根,
∴△=(b﹣2)2=0,解得b=2,
∵f(x﹣1)=f(3﹣x),∴x=1是函数的对称轴,
又此函数图象的对称轴是直线x=﹣,∴﹣=1,∴a=﹣1,
故f(x)=﹣x2+2x;……3分
(2)∵函数f(x)=﹣x2+2x对称轴为x=1,x∈[0,t],
∴当t≤1时,f(x)在[0,t]上是增函数,∴f(x)max=﹣t2+2t,
当t>1时,f(x)在[0,1]上是增函数,在[1,t]上是减函数,∴f(a)max=f(1)=1,
综上,.……3分
(3)∵f(x)=﹣(x﹣1)2+1≤1,∴4n≤1,即n≤.
而抛物线y=﹣x2+2x的对称轴为x=1,∴当n≤时,f(x)在[m,n]上为增函数.
若满足题设条件的m,n存在,则
即 又m<n≤.
∴m=﹣2,n=0,这时,定义域为[﹣2,0],值域为[﹣8,0].
由以上知满足条件的m,n存在,m=﹣2,n=0.……4分
22.解:(1)∵f(x)是奇函数,∴定义域关于原点对称,
由,得(x﹣1)(1﹣ax)>0.
令(x﹣1)(1﹣ax)=0,得x1=1,x2=,∴=﹣1,解得a=﹣1.……3分
(2)令u(x)==1+,设任意x1<x2,且x1, x2∈(1,+∞),
则u(x1)﹣u(x2)=,
∵1<x1<x2,∴x1﹣1>0,x2﹣1>0,x2﹣x1>0,
∴u(x1)﹣u(x2)>0,即u(x1)>u(x2).
∴u(x)=1+(x>1)是减函数,
又为减函数,
∴f(x)=在(1,+∞)上为增函数.……4分
(3)由题意知﹣>m,x∈(3,4)时恒成立,
令g(x)=﹣,x∈(3,4),由(1)知在[3,4]上为增函数,又﹣在(3,4)上也是增函数,
故g(x)在(3,4)上为增函数,
∴g(x)的最小值为g(3)=﹣=﹣,
∴m≤﹣,故实数m的范围是(﹣∞,﹣].……3分
y
x
y
x
O
x
O
x
y
O
x
y
O
同课章节目录
