2023-2024学年北京市中国人民大学附属中学九年级下学期6月月考数学试卷(PDF版,无答案)
文档属性
| 名称 | 2023-2024学年北京市中国人民大学附属中学九年级下学期6月月考数学试卷(PDF版,无答案) |

|
|
| 格式 | |||
| 文件大小 | 580.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-04 00:00:00 | ||
图片预览


文档简介
2024北京人大附中初三 6月月考
数 学
一、选择题:(每题 2分,共 16分)
1. 如图,由 7 个大小相同的小正方体拼成的几何体,其主视图是( )
A. B. C. D.
2. 河北张家口每年可向北京地区输送风能、太阳能、生物质能等绿电约 22500000000 千瓦时,其中数据
22500000000 用科学记数法表示为( )
A. 0.225 1011 B. 2.25 1010 C. 22.5 109 D. 225 108
3. 实数 a,b在数轴上的对应点的位置如图所示,下列结论正确的是( )
A. a b 0 B. a b 0 C. a b D. ab 0
4. 下列运算结果正确的是( )
A. b3 b3 = 2b3 B. ( ab)
2 = ab2 C. a5 a2 = a3 D. a2 + a = a3
5. 一个不透明的口袋中有四张卡片,上面分别写有数字1, 2,3, 4 ,除数字外四张卡片无其他区别.随机从
这个口袋中同时取出两张卡片,卡片上的数字之和等于 5 的概率是( )
1 2 1 3
A. B. C. D.
3 5 2 4
6. 关于 x的方程 x2 x + a 2 = 0有两个不相等的实数根,则实数 a的值可能为( )
A. 2 B. 2.5 C. 3 D. 3.5
7. 下列说法错误的是( )
A. 圆周长 C是半径 r的正比例函数 B. 对角线相等的四边形是矩形
C. 菱形的对角线互相垂直平分 D. 方差越大,波动越大
8. 某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人,则选出的恰为一
男一女的概率是( )
4 3 2 1
A. B. C. D.
5 5 5 5
二、填空题(共 16分,每题 2分)
第1页/共6页
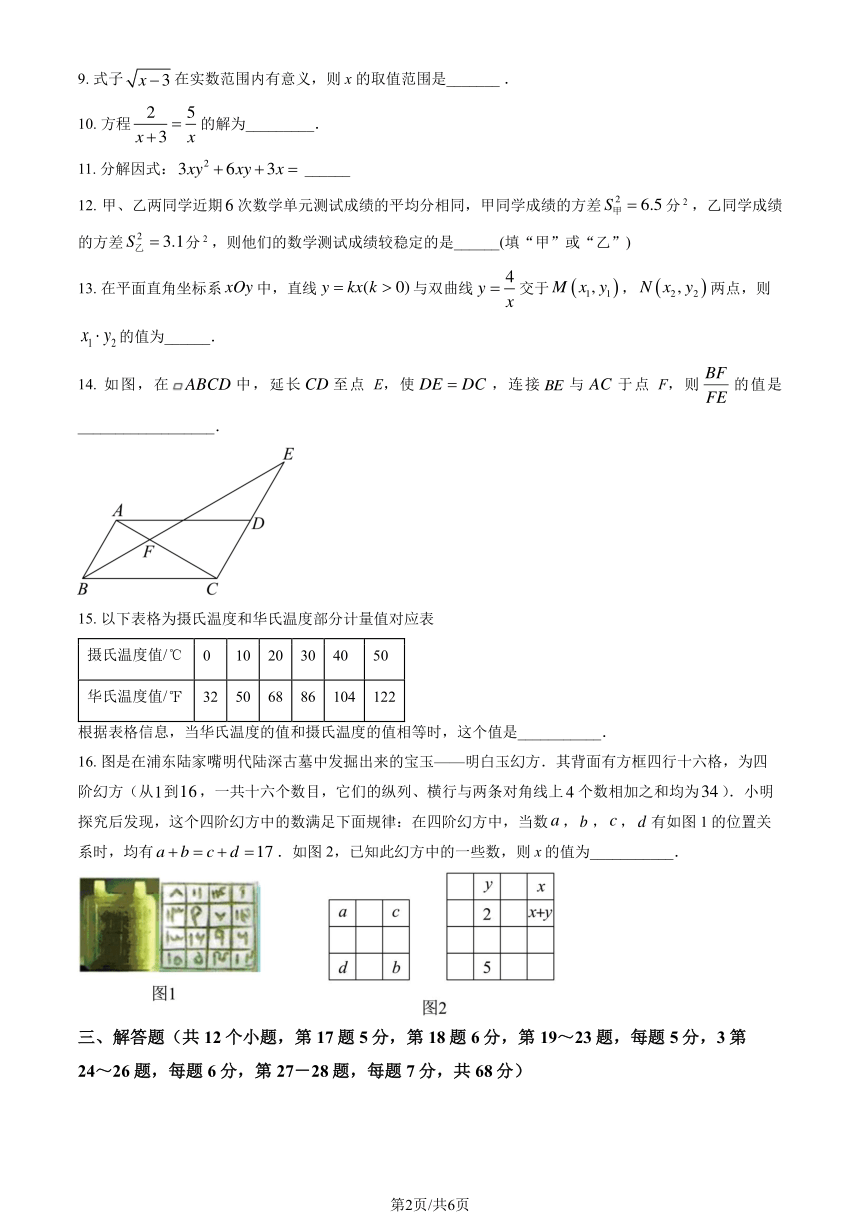
9. 式子 x 3 在实数范围内有意义,则 x 的取值范围是_______ .
2 5
10. 方程 = 的解为_________.
x +3 x
11. 分解因式:3xy2 + 6xy +3x = ______
2
12. 甲、乙两同学近期6 次数学单元测试成绩的平均分相同,甲同学成绩的方差 S甲 = 6.5分
2 ,乙同学成绩
2
的方差 S 2乙 = 3.1分 ,则他们的数学测试成绩较稳定的是______(填“甲”或“乙”)
4
13. 在平面直角坐标系 xOy 中,直线 y = kx(k 0)与双曲线 y = 交于M (x1, y1 ), N (x2 , y2 )两点,则
x
x1 y2 的值为______.
BF
14. 如图,在 ABCD 中,延长 CD 至点 E,使 DE = DC ,连接 BE 与 AC 于点 F,则 的值是
FE
__________________.
15. 以下表格为摄氏温度和华氏温度部分计量值对应表
摄氏温度值/℃ 0 10 20 30 40 50
华氏温度值/℉ 32 50 68 86 104 122
根据表格信息,当华氏温度的值和摄氏温度的值相等时,这个值是___________.
16. 图是在浦东陆家嘴明代陆深古墓中发掘出来的宝玉——明白玉幻方.其背面有方框四行十六格,为四
阶幻方(从1到16,一共十六个数目,它们的纵列、横行与两条对角线上 4 个数相加之和均为34).小明
探究后发现,这个四阶幻方中的数满足下面规律:在四阶幻方中,当数 a,b , c, d 有如图 1 的位置关
系时,均有 a + b = c + d =17 .如图 2,已知此幻方中的一些数,则 x的值为___________.
三、解答题(共 12个小题,第 17题 5分,第 18题 6分,第 19~23题,每题 5分,3第
24~26题,每题 6分,第 27-28题,每题 7分,共 68分)
第2页/共6页
1
0 1
17. 计算: (3 ) + 12 6cos30
4
2x + 6 4
18. 解不等式组: 4x +1 ,并写出该不等式组的非负整数解.
x 1
3
19. 已知 x2
2
3x 2 = 0,求代数式 (x +1)(x 1) (x + 3) + 2x2 的值.
20. 已知关于 x的一元二次方程 x2 mx +m 1= 0.
(1)求证:方程总有两个实数根;
(2)若方程有一个根小于 4,求m 的取值范围.
21. 在平面直角坐标系 xOy 中,一次函数 y = x + b 经过点(0,2).
(1)求这个一次函数的解析式:
(2)当 x 4 时,对于 x的每一个值,函数 y = x + b 的值与函数 y = kx k 的值之和都大于 0,求 k的取
值范围.
22. 如图,在菱形 ABCD中,对角线 AC , BD交于点O ,过点A 作 AE ⊥ BC 于点 E ,延长 BC 到点
F ,使CF = BE ,连接 DF .
(1)求证:四边形 AEFD 是矩形;
(2)连接OE ,若 AD = 10, EC = 4,求OE 的长度.
23. 在△ABF 中,C 为 AF上一点且 AB=AC.
(1)尺规作图:作出以 AB 为直径的⊙O,⊙O 分别交 AC、BC 于点 D、E,在图上标出 D、E,在图上标出
D、E(保留作图痕迹,不写作法).
(2)若∠BAF=2∠CBF,求证:直线 BF 是⊙O 的切线;
5
(3)在(2)中,若 AB=5,sin∠CBF= ,求 BC 和 BF 的长.
5
24. 如图,在Rt ABC 中, ACB = 90 ,D为 AB 的中点,连接CD,过点 A作 AG / /DC ,过点 C作
CG / /DA, AG 与CG 相交于点 G.
第3页/共6页
(1)求证:四边形 ADCG 是菱形
3
(2)若 AB =10, tan CAG = ,求 BC 的长.
4
25. 学校组织九年级学生进行跨学科主题学习活动,利用函数的相关知识研究某种化学试剂的挥发情况.在
两种不同的场景 A和场景 B下做对比实验,设实验过程中,该试剂挥发时间为 x分钟时,在场景 A,B中的
剩余质量分别为 y1 , y2 (单位:克).
下面是某研究小组的探究过程,请补充完整:
记录 y1 , y2 与 x的几组对应值如下:
x(分钟) 0 5 10 15 20 …
y1 (克) 25 23.5 20 14.5 7 …
y2 (克) 25 20 15 10 5 …
(1)在同一平面直角坐标系 xOy 中,描出上表中各组数值所对应的点 (x,y1 ),(x,y2 ),并画出函数
y1,y2 的图象;
(2)进一步探究发现,场景 A的图象是抛物线的一部分, y1 与 x之间近似满足函数关系
y = 0.04x21 +bx + c.场景 B的图象是直线的一部分, y2 与 x之间近似满足函数关系
y2 = ax + c (a 0).请分别求出场景 A,B满足的函数关系式;
(3)查阅文献可知,该化学试剂的质量不低于 4 克时,才能发挥作用.在上述实验中,记该化学试剂在
场景 A,B中发挥作用的时间分别为 xA,xB ,则 xA xB (填“>”,“=”或“<”).
第4页/共6页
26. 如图 1,抛物线 y=ax2+bx+3 过 A(1,0)、B(3,0)两点,交 y轴于点 C.
(1)求抛物线的函数解析式;
(2)在抛物线的对称轴上是否存在点 M,使△ACM的周长最小?若存在,求出△ACM周长的最小值;若
不存在,请说明理由.
(3)如图 2,连接 BC,抛物线上是否存在一点 P,使得∠BCP=∠ACB?若存在,求出点 P的坐标;若不
存在,请说明理由.
27. 已知:Rt ABC中, ACB = 90 , AC = BC .
(1)如图 1,点 D 是 BC 边上一点(不与点 B ,C 重合),连接 AD ,过点 B 作 BE ⊥ AD ,交 AD 的延
长线于点 E ,连接CE .若 BAD = ,求 DBE 的大小(用含 的式子表示);
(2)如图 2,点 D 在线段 BC 的延长线上时,连接 AD ,过点 B 作 BE ⊥ AD ,垂足 E 在线段 AD 上,连
接CE .
①依题意补全图 2;
②用等式表示线段 EA, EB 和 EC 之间的数量关系,并证明.
28. 设平面内一点到等边三角形中心的距离为 d,等边三角形的内切圆半径为 r,外接圆半径为 R .对于一
个点与等边三角形,给出如下定义:满足 r≤d≤R 的点叫做等边三角形的中心关联点.在平面直角坐标系
xOy 中,等边△ABC 的三个顶点的坐标分别为 A(0,2),B(﹣ 3 ,﹣1),C( 3 ,﹣1).
1
(1)已知点 D(2,2),E( 3 ,1),F( - ,﹣1).在 D,E,F 中,是等边△ABC的中心关联点的
2
是 ;
(2)如图 1,过点 A 作直线交 x 轴正半轴于 M,使∠AMO=30°.
①若线段 AM上存在等边△ABC 的中心关联点 P(m,n),求 m的取值范围;
②将直线 AM向下平移得到直线 y=kx+b,当 b 满足什么条件时,直线 y=kx+b 上总.存.在.等边△ABC 的中心关
联点;(直接写出答案,不需过程)
第5页/共6页
1
(3)如图 2,点 Q 为直线 y=﹣1 上一动点,⊙Q的半径为 .当 Q 从点(﹣4,﹣1)出发,以每秒 1个单
2
位的速度向右移动,运动时间为 t秒.是否存在某一时刻 t,使得⊙Q 上所有点都是等边△ABC 的中心关联
点?如果存在,请直接写出所有符合题意的 t的值;如果不存在,请说明理由.
第6页/共6页
数 学
一、选择题:(每题 2分,共 16分)
1. 如图,由 7 个大小相同的小正方体拼成的几何体,其主视图是( )
A. B. C. D.
2. 河北张家口每年可向北京地区输送风能、太阳能、生物质能等绿电约 22500000000 千瓦时,其中数据
22500000000 用科学记数法表示为( )
A. 0.225 1011 B. 2.25 1010 C. 22.5 109 D. 225 108
3. 实数 a,b在数轴上的对应点的位置如图所示,下列结论正确的是( )
A. a b 0 B. a b 0 C. a b D. ab 0
4. 下列运算结果正确的是( )
A. b3 b3 = 2b3 B. ( ab)
2 = ab2 C. a5 a2 = a3 D. a2 + a = a3
5. 一个不透明的口袋中有四张卡片,上面分别写有数字1, 2,3, 4 ,除数字外四张卡片无其他区别.随机从
这个口袋中同时取出两张卡片,卡片上的数字之和等于 5 的概率是( )
1 2 1 3
A. B. C. D.
3 5 2 4
6. 关于 x的方程 x2 x + a 2 = 0有两个不相等的实数根,则实数 a的值可能为( )
A. 2 B. 2.5 C. 3 D. 3.5
7. 下列说法错误的是( )
A. 圆周长 C是半径 r的正比例函数 B. 对角线相等的四边形是矩形
C. 菱形的对角线互相垂直平分 D. 方差越大,波动越大
8. 某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人,则选出的恰为一
男一女的概率是( )
4 3 2 1
A. B. C. D.
5 5 5 5
二、填空题(共 16分,每题 2分)
第1页/共6页
9. 式子 x 3 在实数范围内有意义,则 x 的取值范围是_______ .
2 5
10. 方程 = 的解为_________.
x +3 x
11. 分解因式:3xy2 + 6xy +3x = ______
2
12. 甲、乙两同学近期6 次数学单元测试成绩的平均分相同,甲同学成绩的方差 S甲 = 6.5分
2 ,乙同学成绩
2
的方差 S 2乙 = 3.1分 ,则他们的数学测试成绩较稳定的是______(填“甲”或“乙”)
4
13. 在平面直角坐标系 xOy 中,直线 y = kx(k 0)与双曲线 y = 交于M (x1, y1 ), N (x2 , y2 )两点,则
x
x1 y2 的值为______.
BF
14. 如图,在 ABCD 中,延长 CD 至点 E,使 DE = DC ,连接 BE 与 AC 于点 F,则 的值是
FE
__________________.
15. 以下表格为摄氏温度和华氏温度部分计量值对应表
摄氏温度值/℃ 0 10 20 30 40 50
华氏温度值/℉ 32 50 68 86 104 122
根据表格信息,当华氏温度的值和摄氏温度的值相等时,这个值是___________.
16. 图是在浦东陆家嘴明代陆深古墓中发掘出来的宝玉——明白玉幻方.其背面有方框四行十六格,为四
阶幻方(从1到16,一共十六个数目,它们的纵列、横行与两条对角线上 4 个数相加之和均为34).小明
探究后发现,这个四阶幻方中的数满足下面规律:在四阶幻方中,当数 a,b , c, d 有如图 1 的位置关
系时,均有 a + b = c + d =17 .如图 2,已知此幻方中的一些数,则 x的值为___________.
三、解答题(共 12个小题,第 17题 5分,第 18题 6分,第 19~23题,每题 5分,3第
24~26题,每题 6分,第 27-28题,每题 7分,共 68分)
第2页/共6页
1
0 1
17. 计算: (3 ) + 12 6cos30
4
2x + 6 4
18. 解不等式组: 4x +1 ,并写出该不等式组的非负整数解.
x 1
3
19. 已知 x2
2
3x 2 = 0,求代数式 (x +1)(x 1) (x + 3) + 2x2 的值.
20. 已知关于 x的一元二次方程 x2 mx +m 1= 0.
(1)求证:方程总有两个实数根;
(2)若方程有一个根小于 4,求m 的取值范围.
21. 在平面直角坐标系 xOy 中,一次函数 y = x + b 经过点(0,2).
(1)求这个一次函数的解析式:
(2)当 x 4 时,对于 x的每一个值,函数 y = x + b 的值与函数 y = kx k 的值之和都大于 0,求 k的取
值范围.
22. 如图,在菱形 ABCD中,对角线 AC , BD交于点O ,过点A 作 AE ⊥ BC 于点 E ,延长 BC 到点
F ,使CF = BE ,连接 DF .
(1)求证:四边形 AEFD 是矩形;
(2)连接OE ,若 AD = 10, EC = 4,求OE 的长度.
23. 在△ABF 中,C 为 AF上一点且 AB=AC.
(1)尺规作图:作出以 AB 为直径的⊙O,⊙O 分别交 AC、BC 于点 D、E,在图上标出 D、E,在图上标出
D、E(保留作图痕迹,不写作法).
(2)若∠BAF=2∠CBF,求证:直线 BF 是⊙O 的切线;
5
(3)在(2)中,若 AB=5,sin∠CBF= ,求 BC 和 BF 的长.
5
24. 如图,在Rt ABC 中, ACB = 90 ,D为 AB 的中点,连接CD,过点 A作 AG / /DC ,过点 C作
CG / /DA, AG 与CG 相交于点 G.
第3页/共6页
(1)求证:四边形 ADCG 是菱形
3
(2)若 AB =10, tan CAG = ,求 BC 的长.
4
25. 学校组织九年级学生进行跨学科主题学习活动,利用函数的相关知识研究某种化学试剂的挥发情况.在
两种不同的场景 A和场景 B下做对比实验,设实验过程中,该试剂挥发时间为 x分钟时,在场景 A,B中的
剩余质量分别为 y1 , y2 (单位:克).
下面是某研究小组的探究过程,请补充完整:
记录 y1 , y2 与 x的几组对应值如下:
x(分钟) 0 5 10 15 20 …
y1 (克) 25 23.5 20 14.5 7 …
y2 (克) 25 20 15 10 5 …
(1)在同一平面直角坐标系 xOy 中,描出上表中各组数值所对应的点 (x,y1 ),(x,y2 ),并画出函数
y1,y2 的图象;
(2)进一步探究发现,场景 A的图象是抛物线的一部分, y1 与 x之间近似满足函数关系
y = 0.04x21 +bx + c.场景 B的图象是直线的一部分, y2 与 x之间近似满足函数关系
y2 = ax + c (a 0).请分别求出场景 A,B满足的函数关系式;
(3)查阅文献可知,该化学试剂的质量不低于 4 克时,才能发挥作用.在上述实验中,记该化学试剂在
场景 A,B中发挥作用的时间分别为 xA,xB ,则 xA xB (填“>”,“=”或“<”).
第4页/共6页
26. 如图 1,抛物线 y=ax2+bx+3 过 A(1,0)、B(3,0)两点,交 y轴于点 C.
(1)求抛物线的函数解析式;
(2)在抛物线的对称轴上是否存在点 M,使△ACM的周长最小?若存在,求出△ACM周长的最小值;若
不存在,请说明理由.
(3)如图 2,连接 BC,抛物线上是否存在一点 P,使得∠BCP=∠ACB?若存在,求出点 P的坐标;若不
存在,请说明理由.
27. 已知:Rt ABC中, ACB = 90 , AC = BC .
(1)如图 1,点 D 是 BC 边上一点(不与点 B ,C 重合),连接 AD ,过点 B 作 BE ⊥ AD ,交 AD 的延
长线于点 E ,连接CE .若 BAD = ,求 DBE 的大小(用含 的式子表示);
(2)如图 2,点 D 在线段 BC 的延长线上时,连接 AD ,过点 B 作 BE ⊥ AD ,垂足 E 在线段 AD 上,连
接CE .
①依题意补全图 2;
②用等式表示线段 EA, EB 和 EC 之间的数量关系,并证明.
28. 设平面内一点到等边三角形中心的距离为 d,等边三角形的内切圆半径为 r,外接圆半径为 R .对于一
个点与等边三角形,给出如下定义:满足 r≤d≤R 的点叫做等边三角形的中心关联点.在平面直角坐标系
xOy 中,等边△ABC 的三个顶点的坐标分别为 A(0,2),B(﹣ 3 ,﹣1),C( 3 ,﹣1).
1
(1)已知点 D(2,2),E( 3 ,1),F( - ,﹣1).在 D,E,F 中,是等边△ABC的中心关联点的
2
是 ;
(2)如图 1,过点 A 作直线交 x 轴正半轴于 M,使∠AMO=30°.
①若线段 AM上存在等边△ABC 的中心关联点 P(m,n),求 m的取值范围;
②将直线 AM向下平移得到直线 y=kx+b,当 b 满足什么条件时,直线 y=kx+b 上总.存.在.等边△ABC 的中心关
联点;(直接写出答案,不需过程)
第5页/共6页
1
(3)如图 2,点 Q 为直线 y=﹣1 上一动点,⊙Q的半径为 .当 Q 从点(﹣4,﹣1)出发,以每秒 1个单
2
位的速度向右移动,运动时间为 t秒.是否存在某一时刻 t,使得⊙Q 上所有点都是等边△ABC 的中心关联
点?如果存在,请直接写出所有符合题意的 t的值;如果不存在,请说明理由.
第6页/共6页
同课章节目录
