湘教版数学九年级上册 章节复习课件:第二章 一元二次方程(共12张PPT)
文档属性
| 名称 | 湘教版数学九年级上册 章节复习课件:第二章 一元二次方程(共12张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 14.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-21 11:37:49 | ||
图片预览





文档简介
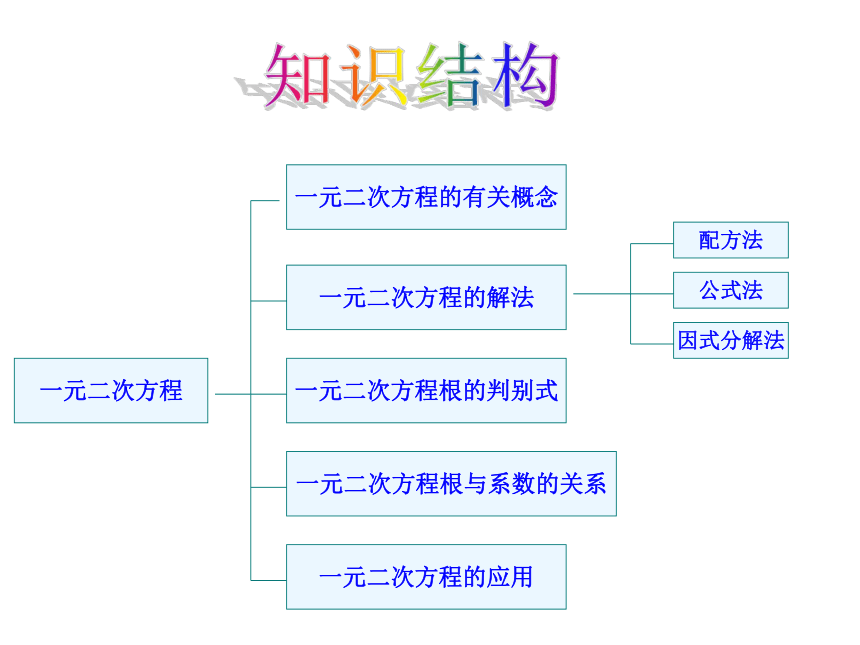
课件12张PPT。单元复习1、什么样的方程是一元二次方程?它的一般
形式是什么?
2、如何运用配方法、公式法、因式分解法解
一元二次方程?
3、如何根据一元二次方程的根的判别式来判
断方程是否有实根?
4、一元二次方程根与系数的关系。
5、利用一元二次方程模型解决实际问题有哪
些步骤?回顾知识结构典例精析,复习新知 1.(1)方程(m+1)xm2-2m-1 +7x-m=0是一元二次方程,则m是多少?
分析:首先根据一元二次方程的定义得,m2-2m-1=2;再由一元二次方程ax2+bx+c=0(a≠0)的定义中a≠0这一条件得m+1≠0来求m的值.
解:m=3.
(2)若关于x的一元二次方程(m-1)x2+5x+m2-3m+2=0的常数项为0,则m等于( )
A.1 B.2 C.1或2 D.0
分析:首先得出m2-3m+2=0;再由一元二次方程ax2+bx+c=0(a≠0)的定义中a≠0这一条件得m-1≠0来求m的值.
解:m=2.
2、用适当的方法解一元二次方程
(1)x2=3x (2)(x-1)2=3
(3)x2-2x-99=0 (4)2x2+5x-3=0
分析: 方程(1)选用因式分解法;方程(2)选用直接开平方法;方程(3)选用配方法;方程(4)选用公式法
3、若(x2+y2)2-4(x2+y2)-5=0,
则x2+y2= 。
分析:用换元法设x2+y2=m得m2-4m-5=0,
解得m1=5 m2=-1
对所求结果,还要结合“x2+y2”进行取舍,从而得到最后结果.
解:x2+y2=5
4、若关于x的一元二次方程kx2-2x-1=0有两不相等的实数根,则k的取值范围是( )
A.k>-1 B. k>-1且 k≠0
C. k<1 D. k<1且k≠0
分析:b2-4ac=(-2)2-4×(-1)k=4k+4>0得k>-1,再由一元二次方程ax2+bx+c=0(a≠0)的定义中a≠0这一条件得k≠0.
解:B5、某商场将销售成本为30元的台灯以40元的价格售出,平均每月销售600个.市场调查表明:这种台灯的售价每上涨1元,每月平均销售数量将减少10个.若销售利润率不得高于100%,那么销售这种台灯每月要获利10 000元,台灯的售价应定为多少元?
分析:如果这种台灯售价上涨x元,那么每个台灯获利(40+x-30)元,每月平均销售数量为(600-10x)个,销售利润为(40+x-30)和 (600-10x)的积.用一元二次方程解决实际问题时,所求得的结果往往有两个,而实际问题的答案常常是一个,这就需要我们仔细审题,看清题目的要求,进而作出正确的选择。
解:设这种台灯的售价上涨x元,根据题意,得
(40+x-30) (600-10x)=10 000.
即x2-50x+400=0 .
解得x1=10,x2=40.
所以每个台灯的售价应定为50元或80元.
当台灯售价定为80元时,销售利润率高于100%,不符合要求;当台灯售价定为50元时,销售利润率不高于100%,符合要求.
答:每个台灯售价应是50。复习训练,巩固提高 1、一元二次方程x2-2x-1=0的根的情况为( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.只有一个实数根
D.没有实数根
分析:b2-4ac=(-2)2-4×(-1)=8>0
解:B2、已知关于x的方程x2+(2k+1)x+k2-2=0的两实根的平 方和等于11,则k的值为 .
分析:设方程方程x2+(2k+1)x+k2﹣2=0设其两根为x1,x2,得
∵△=(2k+1)2﹣4×(k2﹣2)=4k+9>0, ∴k>﹣ 。
∵x1+x2=﹣(2k+1),x1?x2=k2﹣2,
又∵x12+x22=11,
∴(x1+x2)2﹣2x1x2=11。
∴(2k+1)2﹣2(k2﹣2)=11,
解得k=1或﹣3。
∵k>﹣ ,∴k=1。
3、若关于x的一元二次方程x2+2x+a=0有实数根,则a的取值范围是_ .
分析:∵关于x的一元二次方程有实根,∴△= ,解之得a≤1。
师生互动,课堂小结 1、回顾整理今日收获。
2、你还有哪些困惑和疑问?
学而时习之,不亦说乎?1.布置作业:从教材习题中选取。 2.完成创优作业本课时的习题。
形式是什么?
2、如何运用配方法、公式法、因式分解法解
一元二次方程?
3、如何根据一元二次方程的根的判别式来判
断方程是否有实根?
4、一元二次方程根与系数的关系。
5、利用一元二次方程模型解决实际问题有哪
些步骤?回顾知识结构典例精析,复习新知 1.(1)方程(m+1)xm2-2m-1 +7x-m=0是一元二次方程,则m是多少?
分析:首先根据一元二次方程的定义得,m2-2m-1=2;再由一元二次方程ax2+bx+c=0(a≠0)的定义中a≠0这一条件得m+1≠0来求m的值.
解:m=3.
(2)若关于x的一元二次方程(m-1)x2+5x+m2-3m+2=0的常数项为0,则m等于( )
A.1 B.2 C.1或2 D.0
分析:首先得出m2-3m+2=0;再由一元二次方程ax2+bx+c=0(a≠0)的定义中a≠0这一条件得m-1≠0来求m的值.
解:m=2.
2、用适当的方法解一元二次方程
(1)x2=3x (2)(x-1)2=3
(3)x2-2x-99=0 (4)2x2+5x-3=0
分析: 方程(1)选用因式分解法;方程(2)选用直接开平方法;方程(3)选用配方法;方程(4)选用公式法
3、若(x2+y2)2-4(x2+y2)-5=0,
则x2+y2= 。
分析:用换元法设x2+y2=m得m2-4m-5=0,
解得m1=5 m2=-1
对所求结果,还要结合“x2+y2”进行取舍,从而得到最后结果.
解:x2+y2=5
4、若关于x的一元二次方程kx2-2x-1=0有两不相等的实数根,则k的取值范围是( )
A.k>-1 B. k>-1且 k≠0
C. k<1 D. k<1且k≠0
分析:b2-4ac=(-2)2-4×(-1)k=4k+4>0得k>-1,再由一元二次方程ax2+bx+c=0(a≠0)的定义中a≠0这一条件得k≠0.
解:B5、某商场将销售成本为30元的台灯以40元的价格售出,平均每月销售600个.市场调查表明:这种台灯的售价每上涨1元,每月平均销售数量将减少10个.若销售利润率不得高于100%,那么销售这种台灯每月要获利10 000元,台灯的售价应定为多少元?
分析:如果这种台灯售价上涨x元,那么每个台灯获利(40+x-30)元,每月平均销售数量为(600-10x)个,销售利润为(40+x-30)和 (600-10x)的积.用一元二次方程解决实际问题时,所求得的结果往往有两个,而实际问题的答案常常是一个,这就需要我们仔细审题,看清题目的要求,进而作出正确的选择。
解:设这种台灯的售价上涨x元,根据题意,得
(40+x-30) (600-10x)=10 000.
即x2-50x+400=0 .
解得x1=10,x2=40.
所以每个台灯的售价应定为50元或80元.
当台灯售价定为80元时,销售利润率高于100%,不符合要求;当台灯售价定为50元时,销售利润率不高于100%,符合要求.
答:每个台灯售价应是50。复习训练,巩固提高 1、一元二次方程x2-2x-1=0的根的情况为( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.只有一个实数根
D.没有实数根
分析:b2-4ac=(-2)2-4×(-1)=8>0
解:B2、已知关于x的方程x2+(2k+1)x+k2-2=0的两实根的平 方和等于11,则k的值为 .
分析:设方程方程x2+(2k+1)x+k2﹣2=0设其两根为x1,x2,得
∵△=(2k+1)2﹣4×(k2﹣2)=4k+9>0, ∴k>﹣ 。
∵x1+x2=﹣(2k+1),x1?x2=k2﹣2,
又∵x12+x22=11,
∴(x1+x2)2﹣2x1x2=11。
∴(2k+1)2﹣2(k2﹣2)=11,
解得k=1或﹣3。
∵k>﹣ ,∴k=1。
3、若关于x的一元二次方程x2+2x+a=0有实数根,则a的取值范围是_ .
分析:∵关于x的一元二次方程有实根,∴△= ,解之得a≤1。
师生互动,课堂小结 1、回顾整理今日收获。
2、你还有哪些困惑和疑问?
学而时习之,不亦说乎?1.布置作业:从教材习题中选取。 2.完成创优作业本课时的习题。
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
