湘教版数学九年级上册 课件: 3.5 相似三角形的应用(共29张PPT)
文档属性
| 名称 | 湘教版数学九年级上册 课件: 3.5 相似三角形的应用(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 858.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-21 12:45:02 | ||
图片预览






文档简介
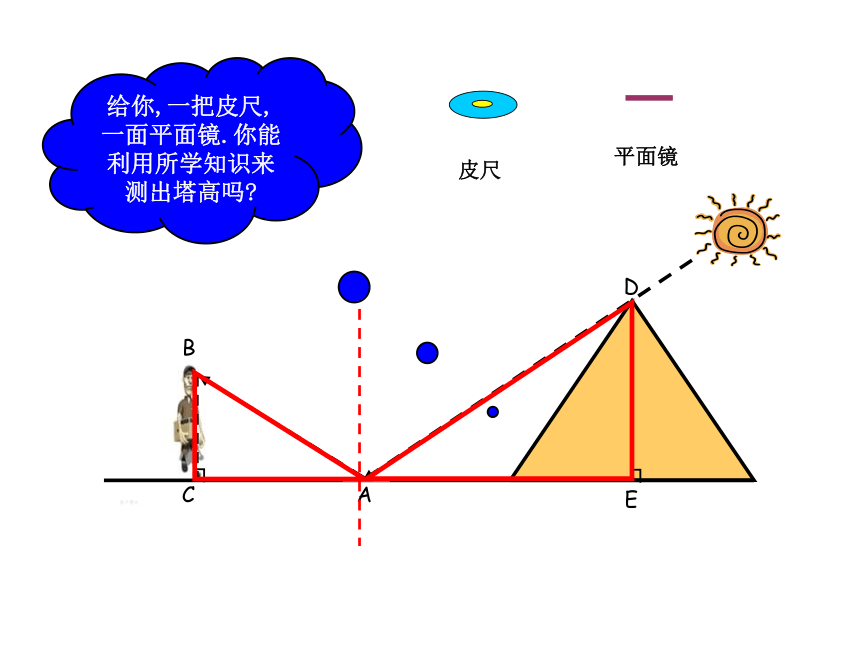
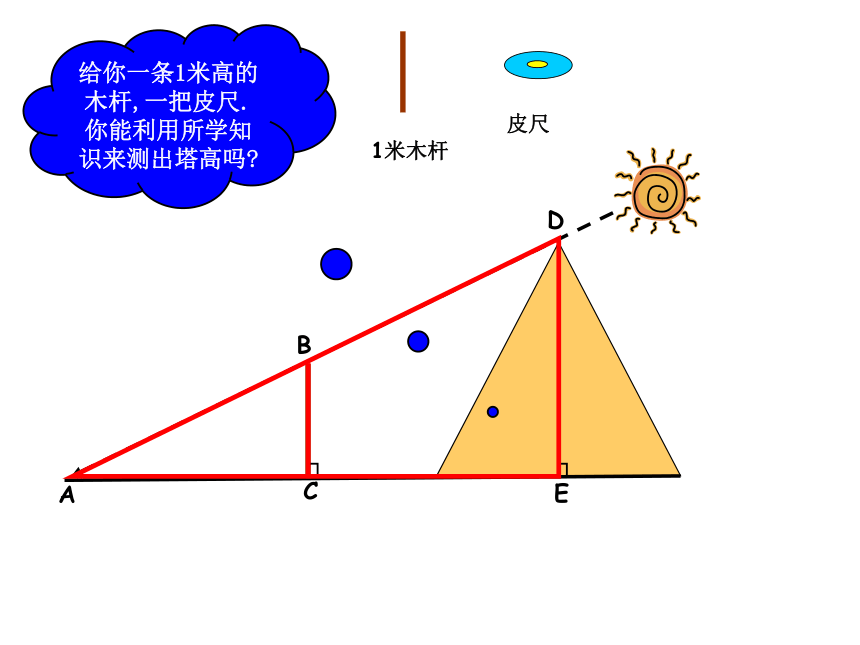
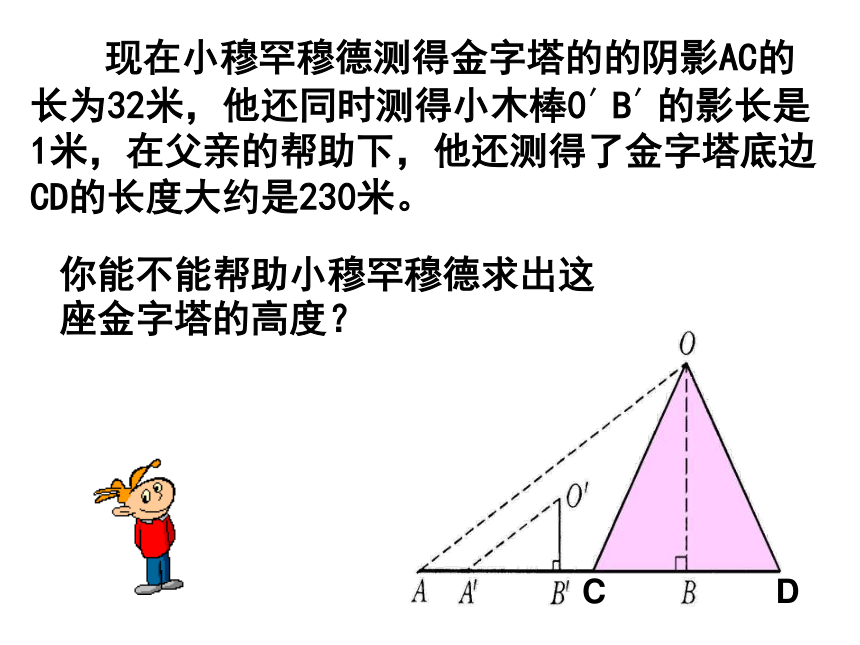
课件29张PPT。3.5 相似三角形的应用太阳光线可以看成是平行光线。 在阳光下,在同一时刻,物体的高度与物体的影长存在某种关系:物体的高度越高,物体的影长就越长 在平行光线的照射下,不同物体的物高与影长成比例 胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。 走近金字塔 埃及著名的考古专家穆罕穆德决定重新测量胡夫金字塔的高度.在一个烈日高照的上午.他和儿子小穆罕穆德来到了金字塔脚下,他想考一考年仅14岁的小穆罕穆德.给你一条1米高的木杆,一把皮尺, 你能利用所学知识来测出塔高吗?1米木杆皮尺ACBDE┐┐给你,一把皮尺,一面平面镜.你能利用所学知识来测出塔高吗?皮尺平面镜ACBDE┐┐给你一条1米高的木杆,一把皮尺.你能利用所学知识来测出塔高吗?1米木杆皮尺 现在小穆罕穆德测得金字塔的的阴影AC的长为32米,他还同时测得小木棒0′B′的影长是1米,在父亲的帮助下,他还测得了金字塔底边CD的长度大约是230米。你能不能帮助小穆罕穆德求出这座金字塔的高度?CD例1 古代一位数学家想出了一种测量金字塔高度的方法:如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与金字塔的影长AB,即可近似算出金字塔的高度OB.如果O ′B′ =1,A′B′=2,AB=274,求金字塔的高度OB.
如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与金字塔影长AB,即可近似算出金字塔的高度OB.如果O′B′=1,A′B′=2,AB=274,求金字塔的高度OB.
答:该金字塔高度OB为137米.
(米)解:∵太阳光是平行光线,∴ ∠OAB=∠O′A′B′.又∵ ∠ABO=∠A′B′O′=90°.∴ △OAB∽△O′A′B′,OB∶O′B′=AB∶A′B′,OB=
物1高 :物2高 = 影1长 :影2长测高的方法 测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成正比例”的原理解决。 变式1.某同学想利用树影测量树高.他在某一时刻测得小树高为1.5米时,其影长为1.2米,当他测量教学楼旁的一棵大树影长时,因大树靠近教学楼,有一部分影子在墙上.经测量,地面部分影长为6.4米,墙上影长为1.4米,那么这棵大树高多少米?D6.41.2?1.51.4ABc解:作DE⊥AB于E
得
∴AE=8
∴AB=8+1.4=9.4米运用物体的影长不等于地上的部分加上墙上的部分甲拓展: 已知教学楼高为12米,在距教学楼9米的北面有一建筑物乙,此时教学楼会影响乙的采光吗?129.6DE运用AFEBO┐┐还可以有其他方法测量吗?一题多解=△ABO∽△AEFOB =平面镜如图,要测量池塘AB的宽度,但由于条件限制无法直接测量,你能想出可行的测量方法吗? 1、在池塘外取一点P 2、过点P做线段PC、PD,使PD:PB=PC:PA=k 3、连接并测量CD长度,即可知AB长度。 证明: ∵在△APB和△DPC中 PD:PB=PC:PA ∠APB=∠DPC ∴△APB ∽ △CPD(SAS) ∴AB:CD=AP:PC=1/K例 在用枪瞄准目标点B时,要使眼睛O、准星A、目标B在同一条直线上,如图所示,在射击时,李明有轻微的抖动,致使准星A偏离到A′,若OA=0.2米,OB=50米,AA′=0.0005米,则李明射击到的点B′偏离目标点B的长度BB′(近似地认为AA′ // BB′ )解:
答:李明射击到的点B′偏离目标点B的长度BB′ 为0.125m 例:如图:为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.A
方法一: 如图:为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.ABCDE解:∵ ∠ ADB = ∠ EDC
∠ ABC =∠ECD =900.
∴ △ABD ∽ △ECD
∴AB︰EC=BD︰CD
∴ AB =BD×EC/CD
=120×50/60
=100(米)
答:两岸间的大致距离为100米。 方法二:我们还可以在河对岸选定一目标点A,再在河的一边选点D和 E,使DE⊥AD,然后,再选点B,作BC∥DE,与视线EA相交于点C。此时,测得DE , BC, BD, 就可以求两岸间的大致距离AB了。此时如果测得DE=120米,BC=60米,BD=50米,求两岸间的大致距离AB.测量河的宽度测量原理:测量不能直接到达的两点间的距离,常构造相似三角形求解。
测量方法:为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD,DC,EC的长,根据相似三角形对应边的比求出河宽AB.
测距的方法 测量不能到达两点间的距离,常构造相似三角形求解。 1. 相似三角形的应用主要有两个方面:(1) 测高 测量不能到达两点间的距离,常构造相似三角形求解。(不能直接使用皮尺或刻度尺量的)(不能直接测量的两点间的距离) 测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决。(2) 测距课堂小结2. 解相似三角形实际问题的一般步骤:(1)审题。
(2)构建图形。
(3)利用相似解决问题。实例运用:利用标杆测量物体的高度 ②如图 27-2-17(2)利用“标杆和视角”构建三角形,其数
学模型为:
图 27-2-17(2)课堂小结:3.相似三角形的应用的主要图形
课 后 作 业1.布置作业:从教材“习题”中选取.
2.完成创优作业中本课时对应习题.
如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与金字塔影长AB,即可近似算出金字塔的高度OB.如果O′B′=1,A′B′=2,AB=274,求金字塔的高度OB.
答:该金字塔高度OB为137米.
(米)解:∵太阳光是平行光线,∴ ∠OAB=∠O′A′B′.又∵ ∠ABO=∠A′B′O′=90°.∴ △OAB∽△O′A′B′,OB∶O′B′=AB∶A′B′,OB=
物1高 :物2高 = 影1长 :影2长测高的方法 测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成正比例”的原理解决。 变式1.某同学想利用树影测量树高.他在某一时刻测得小树高为1.5米时,其影长为1.2米,当他测量教学楼旁的一棵大树影长时,因大树靠近教学楼,有一部分影子在墙上.经测量,地面部分影长为6.4米,墙上影长为1.4米,那么这棵大树高多少米?D6.41.2?1.51.4ABc解:作DE⊥AB于E
得
∴AE=8
∴AB=8+1.4=9.4米运用物体的影长不等于地上的部分加上墙上的部分甲拓展: 已知教学楼高为12米,在距教学楼9米的北面有一建筑物乙,此时教学楼会影响乙的采光吗?129.6DE运用AFEBO┐┐还可以有其他方法测量吗?一题多解=△ABO∽△AEFOB =平面镜如图,要测量池塘AB的宽度,但由于条件限制无法直接测量,你能想出可行的测量方法吗? 1、在池塘外取一点P 2、过点P做线段PC、PD,使PD:PB=PC:PA=k 3、连接并测量CD长度,即可知AB长度。 证明: ∵在△APB和△DPC中 PD:PB=PC:PA ∠APB=∠DPC ∴△APB ∽ △CPD(SAS) ∴AB:CD=AP:PC=1/K例 在用枪瞄准目标点B时,要使眼睛O、准星A、目标B在同一条直线上,如图所示,在射击时,李明有轻微的抖动,致使准星A偏离到A′,若OA=0.2米,OB=50米,AA′=0.0005米,则李明射击到的点B′偏离目标点B的长度BB′(近似地认为AA′ // BB′ )解:
答:李明射击到的点B′偏离目标点B的长度BB′ 为0.125m 例:如图:为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.A
方法一: 如图:为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.ABCDE解:∵ ∠ ADB = ∠ EDC
∠ ABC =∠ECD =900.
∴ △ABD ∽ △ECD
∴AB︰EC=BD︰CD
∴ AB =BD×EC/CD
=120×50/60
=100(米)
答:两岸间的大致距离为100米。 方法二:我们还可以在河对岸选定一目标点A,再在河的一边选点D和 E,使DE⊥AD,然后,再选点B,作BC∥DE,与视线EA相交于点C。此时,测得DE , BC, BD, 就可以求两岸间的大致距离AB了。此时如果测得DE=120米,BC=60米,BD=50米,求两岸间的大致距离AB.测量河的宽度测量原理:测量不能直接到达的两点间的距离,常构造相似三角形求解。
测量方法:为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD,DC,EC的长,根据相似三角形对应边的比求出河宽AB.
测距的方法 测量不能到达两点间的距离,常构造相似三角形求解。 1. 相似三角形的应用主要有两个方面:(1) 测高 测量不能到达两点间的距离,常构造相似三角形求解。(不能直接使用皮尺或刻度尺量的)(不能直接测量的两点间的距离) 测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决。(2) 测距课堂小结2. 解相似三角形实际问题的一般步骤:(1)审题。
(2)构建图形。
(3)利用相似解决问题。实例运用:利用标杆测量物体的高度 ②如图 27-2-17(2)利用“标杆和视角”构建三角形,其数
学模型为:
图 27-2-17(2)课堂小结:3.相似三角形的应用的主要图形
课 后 作 业1.布置作业:从教材“习题”中选取.
2.完成创优作业中本课时对应习题.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
