2024-2025学年黑龙江省哈尔滨市南岗区萧红中学九年级(上)开学数学试卷(五四学制)(含答案)
文档属性
| 名称 | 2024-2025学年黑龙江省哈尔滨市南岗区萧红中学九年级(上)开学数学试卷(五四学制)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 130.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-05 09:59:33 | ||
图片预览



文档简介
2024-2025学年黑龙江省哈尔滨市南岗区萧红中学九年级(上)开学
数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列方程中,属于一元二次方程的是( )
A. B. C. D.
2.下列各曲线中表示是的函数的是( )
A. B. C. D.
3.在下列长度的各组线段中,不能构成直角三角形的是( )
A. ,, B. ,, C. ,, D. ,,
4.在 中,比大,则的度数为( )
A. B. C. D.
5.一次函数的图象经过( )
A. 第一、二、三象限 B. 第一、二、四象限 C. 第一、三、四象限 D. 第二、三、四象限
6.顺次连接矩形四边中点得到的四边形一定是( )
A. 矩形 B. 菱形 C. 等腰梯形 D. 正方形
7.某商场对商场中现有空调进行两次提价,提价后的价格为提价前的,则平均每次提价的百分数为( )
A. B. C. D.
8.如图,在正方形外侧作等边三角形,则的度数为( )
A.
B.
C.
D.
9.给出以下四个命题:
对角线相等的四边形是矩形;
对角线互相垂直的四边形是菱形;
对角线互相垂直的矩形是正方形;
菱形对角线的平方和等于边长平方的倍其中真命题有个.
A. B. C. D.
10.如图,在 中,点在对角线上,,交于点,,交于点,则下列式子一定正确的是( )
A. B. C. D.
二、填空题:本题共10小题,每小题3分,共30分。
11.函数中自变量的取值范围是______.
12.方程的根是______.
13.一次函数中,随的增大而减小,则的取值范围是________.
14.若关于的一元二次方程有两个相等的实数根,则实数的取值范围是______.
15.如图,已知,于点点对应的数是,点对应的数是,,那么数轴上点所表示的数是______.
16.已知直角三角形两边的长分别为和,则第三边的长为______.
17.如图,一次函数的图象与轴交于点,与轴交于点,则不等式的解集为______.
18.如图,四边形是菱形,对角线、相交于点,于点,
连接,,则的度数为______.
19.中,,,,则______.
20.如图,正方形中,点在上,点在上,,连接交于点,若,,则的长是______.
三、解答题:本题共7小题,共60分。解答应写出文字说明,证明过程或演算步骤。
21.本小题分
解方程:.
22.本小题分
图,图中的小正方形的边长均为,线段,的端点,,,均在小正方形的顶点上.
在图中画出一个以线段为边的平行四边形,点,均在小正方形的顶点上,且平行四边形的面积为;
在图中画出以线段为边的菱形,点,均在小正方形的顶点上,且菱形的面积为,连接,直接写出的长.
23.本小题分
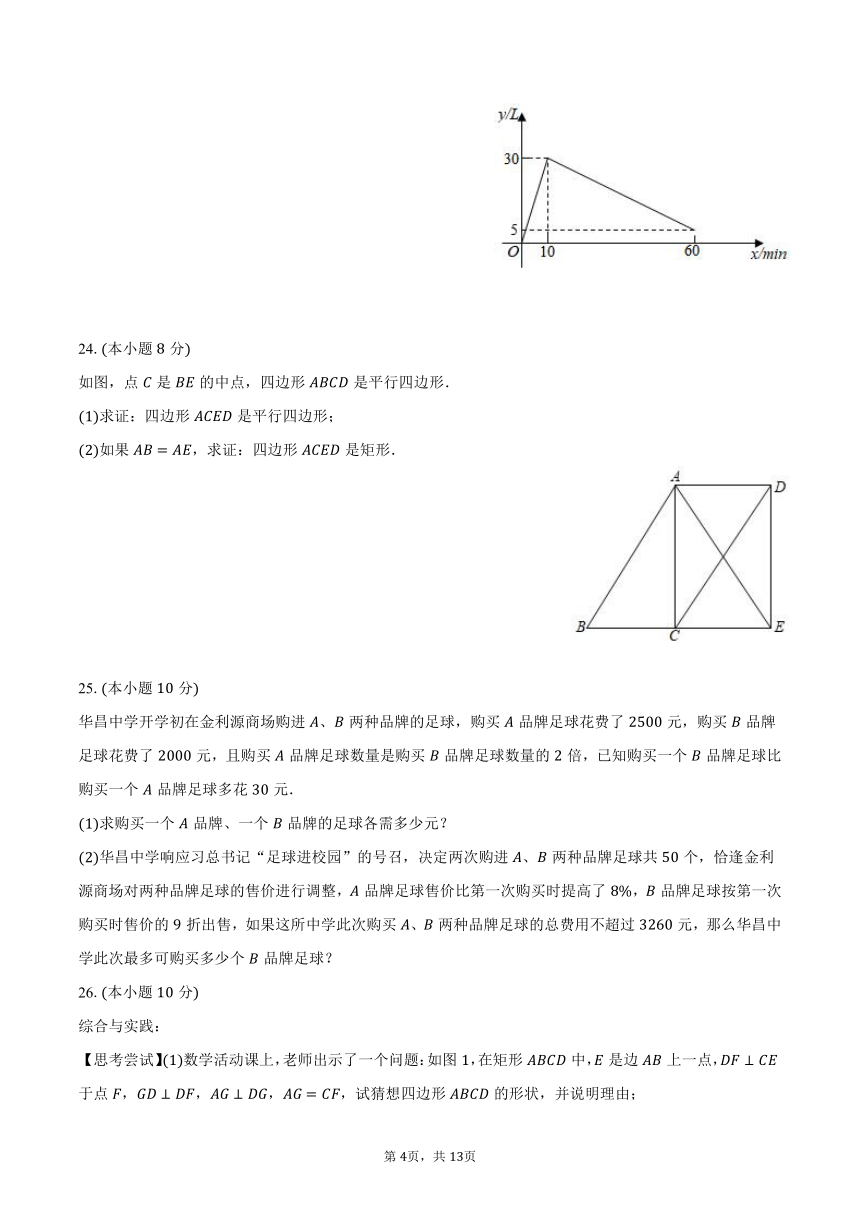
某种机器工作前先将空油箱加满,然后停止加油立即开始工作当停止工作时,油箱中油量为,在整个过程中,油箱里的油量单位:与时间单位:之间的关系如图所示.
填空:机器每分钟加油量为______,机器工作的过程中每分钟耗油量为______;
求机器工作时关于的函数解析式,并写出自变量的取值范围.
24.本小题分
如图,点是的中点,四边形是平行四边形.
求证:四边形是平行四边形;
如果,求证:四边形是矩形.
25.本小题分
华昌中学开学初在金利源商场购进、两种品牌的足球,购买品牌足球花费了元,购买品牌足球花费了元,且购买品牌足球数量是购买品牌足球数量的倍,已知购买一个品牌足球比购买一个品牌足球多花元.
求购买一个品牌、一个品牌的足球各需多少元?
华昌中学响应习总书记“足球进校园”的号召,决定两次购进、两种品牌足球共个,恰逢金利源商场对两种品牌足球的售价进行调整,品牌足球售价比第一次购买时提高了,品牌足球按第一次购买时售价的折出售,如果这所中学此次购买、两种品牌足球的总费用不超过元,那么华昌中学此次最多可购买多少个品牌足球?
26.本小题分
综合与实践:
【思考尝试】数学活动课上,老师出示了一个问题:如图,在矩形中,是边上一点,于点,,,,试猜想四边形的形状,并说明理由;
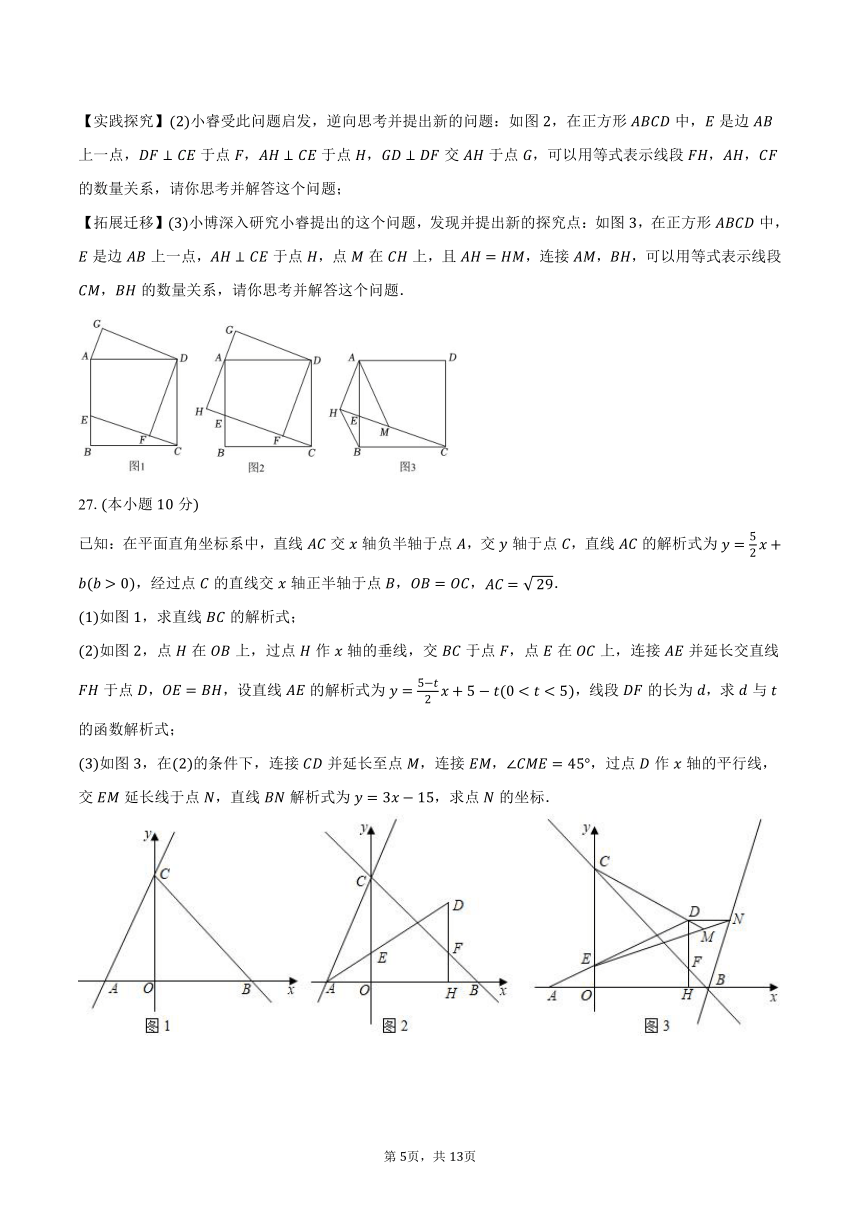
【实践探究】小睿受此问题启发,逆向思考并提出新的问题:如图,在正方形中,是边上一点,于点,于点,交于点,可以用等式表示线段,,的数量关系,请你思考并解答这个问题;
【拓展迁移】小博深入研究小睿提出的这个问题,发现并提出新的探究点:如图,在正方形中,是边上一点,于点,点在上,且,连接,,可以用等式表示线段,的数量关系,请你思考并解答这个问题.
27.本小题分
已知:在平面直角坐标系中,直线交轴负半轴于点,交轴于点,直线的解析式为,经过点的直线交轴正半轴于点,,.
如图,求直线的解析式;
如图,点在上,过点作轴的垂线,交于点,点在上,连接并延长交直线于点,,设直线的解析式为,线段的长为,求与的函数解析式;
如图,在的条件下,连接并延长至点,连接,,过点作轴的平行线,交延长线于点,直线解析式为,求点的坐标.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.或
17.
18.
19.或
20.
21.解:方程化为,
,,,
,
方程有两个不等的实数根,
,
即,.
22.解:如图,四边形即为所求;
如图,四边形即为所求..
23.,;
当时,设关于的函数解析式为,
有图象可得:,
解得:,
,
即机器工作时关于的函数解析式为.
24.解:证明:四边形是平行四边形,
,且.
点是的中点,
,
,
,
四边形是平行四边形;
证明:四边形是平行四边形,
,
,
,
四边形是平行四边形,
四边形是矩形.
25.解:设购买一个品牌的足球需元,则购买一个品牌的足球需元,由题意得
解得:
经检验是原方程的解,
答:一个品牌的足球需元,则一个品牌的足球需元.
设此次可购买个品牌足球,则购进牌足球个,由题意得
解得
因为是整数,
所以最大等于,
答:华昌中学此次最多可购买个品牌足球.
26.解:四边形是正方形,
理由:四边形是矩形,
,
,
,
,
又,,
≌,
,
矩形是正方形;
,
理由:于点,于点,交于点,
四边形是矩形,
,
四边形是正方形,
,,
,
≌,
,,
矩形是正方形,
;
连接,
四边形是正方形,,
,,
是等腰直角三角形,
,
,
,
∽,
,
即.
27.解:当时,,
,
,
当时,,
解得,,
,
,
在中,,,
,
解得:.
,.
,
.
,
设直线的解析式为,
,
解得:,.
直线的解析式为:;
当时,
,
,
,,
,
轴,
,
,
,
,
,
点的横坐标为,
点的纵坐标为,
,
;
过点作,连接并延长交于点,连接,
过点作交的延长线于,
,,
四边形为矩形.
轴.
轴,
,
四边形为矩形,
,,
,
四边形为矩形,
,
,
,
四边形为正方形,
,,
,
,
,
,
即,
,
≌,
,,
,
,
,
,
又,
四边形为平行四边形,
,
,
由知,轴,
点的纵坐标为,
直线的解析式为,,
解得:,
,
,,
,
,
解得:,不合题意,舍去,
.
第1页,共1页
数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列方程中,属于一元二次方程的是( )
A. B. C. D.
2.下列各曲线中表示是的函数的是( )
A. B. C. D.
3.在下列长度的各组线段中,不能构成直角三角形的是( )
A. ,, B. ,, C. ,, D. ,,
4.在 中,比大,则的度数为( )
A. B. C. D.
5.一次函数的图象经过( )
A. 第一、二、三象限 B. 第一、二、四象限 C. 第一、三、四象限 D. 第二、三、四象限
6.顺次连接矩形四边中点得到的四边形一定是( )
A. 矩形 B. 菱形 C. 等腰梯形 D. 正方形
7.某商场对商场中现有空调进行两次提价,提价后的价格为提价前的,则平均每次提价的百分数为( )
A. B. C. D.
8.如图,在正方形外侧作等边三角形,则的度数为( )
A.
B.
C.
D.
9.给出以下四个命题:
对角线相等的四边形是矩形;
对角线互相垂直的四边形是菱形;
对角线互相垂直的矩形是正方形;
菱形对角线的平方和等于边长平方的倍其中真命题有个.
A. B. C. D.
10.如图,在 中,点在对角线上,,交于点,,交于点,则下列式子一定正确的是( )
A. B. C. D.
二、填空题:本题共10小题,每小题3分,共30分。
11.函数中自变量的取值范围是______.
12.方程的根是______.
13.一次函数中,随的增大而减小,则的取值范围是________.
14.若关于的一元二次方程有两个相等的实数根,则实数的取值范围是______.
15.如图,已知,于点点对应的数是,点对应的数是,,那么数轴上点所表示的数是______.
16.已知直角三角形两边的长分别为和,则第三边的长为______.
17.如图,一次函数的图象与轴交于点,与轴交于点,则不等式的解集为______.
18.如图,四边形是菱形,对角线、相交于点,于点,
连接,,则的度数为______.
19.中,,,,则______.
20.如图,正方形中,点在上,点在上,,连接交于点,若,,则的长是______.
三、解答题:本题共7小题,共60分。解答应写出文字说明,证明过程或演算步骤。
21.本小题分
解方程:.
22.本小题分
图,图中的小正方形的边长均为,线段,的端点,,,均在小正方形的顶点上.
在图中画出一个以线段为边的平行四边形,点,均在小正方形的顶点上,且平行四边形的面积为;
在图中画出以线段为边的菱形,点,均在小正方形的顶点上,且菱形的面积为,连接,直接写出的长.
23.本小题分
某种机器工作前先将空油箱加满,然后停止加油立即开始工作当停止工作时,油箱中油量为,在整个过程中,油箱里的油量单位:与时间单位:之间的关系如图所示.
填空:机器每分钟加油量为______,机器工作的过程中每分钟耗油量为______;
求机器工作时关于的函数解析式,并写出自变量的取值范围.
24.本小题分
如图,点是的中点,四边形是平行四边形.
求证:四边形是平行四边形;
如果,求证:四边形是矩形.
25.本小题分
华昌中学开学初在金利源商场购进、两种品牌的足球,购买品牌足球花费了元,购买品牌足球花费了元,且购买品牌足球数量是购买品牌足球数量的倍,已知购买一个品牌足球比购买一个品牌足球多花元.
求购买一个品牌、一个品牌的足球各需多少元?
华昌中学响应习总书记“足球进校园”的号召,决定两次购进、两种品牌足球共个,恰逢金利源商场对两种品牌足球的售价进行调整,品牌足球售价比第一次购买时提高了,品牌足球按第一次购买时售价的折出售,如果这所中学此次购买、两种品牌足球的总费用不超过元,那么华昌中学此次最多可购买多少个品牌足球?
26.本小题分
综合与实践:
【思考尝试】数学活动课上,老师出示了一个问题:如图,在矩形中,是边上一点,于点,,,,试猜想四边形的形状,并说明理由;
【实践探究】小睿受此问题启发,逆向思考并提出新的问题:如图,在正方形中,是边上一点,于点,于点,交于点,可以用等式表示线段,,的数量关系,请你思考并解答这个问题;
【拓展迁移】小博深入研究小睿提出的这个问题,发现并提出新的探究点:如图,在正方形中,是边上一点,于点,点在上,且,连接,,可以用等式表示线段,的数量关系,请你思考并解答这个问题.
27.本小题分
已知:在平面直角坐标系中,直线交轴负半轴于点,交轴于点,直线的解析式为,经过点的直线交轴正半轴于点,,.
如图,求直线的解析式;
如图,点在上,过点作轴的垂线,交于点,点在上,连接并延长交直线于点,,设直线的解析式为,线段的长为,求与的函数解析式;
如图,在的条件下,连接并延长至点,连接,,过点作轴的平行线,交延长线于点,直线解析式为,求点的坐标.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.或
17.
18.
19.或
20.
21.解:方程化为,
,,,
,
方程有两个不等的实数根,
,
即,.
22.解:如图,四边形即为所求;
如图,四边形即为所求..
23.,;
当时,设关于的函数解析式为,
有图象可得:,
解得:,
,
即机器工作时关于的函数解析式为.
24.解:证明:四边形是平行四边形,
,且.
点是的中点,
,
,
,
四边形是平行四边形;
证明:四边形是平行四边形,
,
,
,
四边形是平行四边形,
四边形是矩形.
25.解:设购买一个品牌的足球需元,则购买一个品牌的足球需元,由题意得
解得:
经检验是原方程的解,
答:一个品牌的足球需元,则一个品牌的足球需元.
设此次可购买个品牌足球,则购进牌足球个,由题意得
解得
因为是整数,
所以最大等于,
答:华昌中学此次最多可购买个品牌足球.
26.解:四边形是正方形,
理由:四边形是矩形,
,
,
,
,
又,,
≌,
,
矩形是正方形;
,
理由:于点,于点,交于点,
四边形是矩形,
,
四边形是正方形,
,,
,
≌,
,,
矩形是正方形,
;
连接,
四边形是正方形,,
,,
是等腰直角三角形,
,
,
,
∽,
,
即.
27.解:当时,,
,
,
当时,,
解得,,
,
,
在中,,,
,
解得:.
,.
,
.
,
设直线的解析式为,
,
解得:,.
直线的解析式为:;
当时,
,
,
,,
,
轴,
,
,
,
,
,
点的横坐标为,
点的纵坐标为,
,
;
过点作,连接并延长交于点,连接,
过点作交的延长线于,
,,
四边形为矩形.
轴.
轴,
,
四边形为矩形,
,,
,
四边形为矩形,
,
,
,
四边形为正方形,
,,
,
,
,
,
即,
,
≌,
,,
,
,
,
,
又,
四边形为平行四边形,
,
,
由知,轴,
点的纵坐标为,
直线的解析式为,,
解得:,
,
,,
,
,
解得:,不合题意,舍去,
.
第1页,共1页
同课章节目录
