7.1.2 全概率公式 课件 (共18张PPT )2024-2025学年 人教A版(2019)选择性必修第三册
文档属性
| 名称 | 7.1.2 全概率公式 课件 (共18张PPT )2024-2025学年 人教A版(2019)选择性必修第三册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 865.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-06 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
§7.1.2 全概率公式与贝叶斯公式
解
四、全概率公式
因为 B=AB +
,且AB与
互不相容,所以
= 0.6
一个盒子中有6只白球、4只黑球,从中不放回地每次任取1只,连取2次,求第二次取到白球的概率
例
A=“第一次取到白球” B=“第二次取到白球”
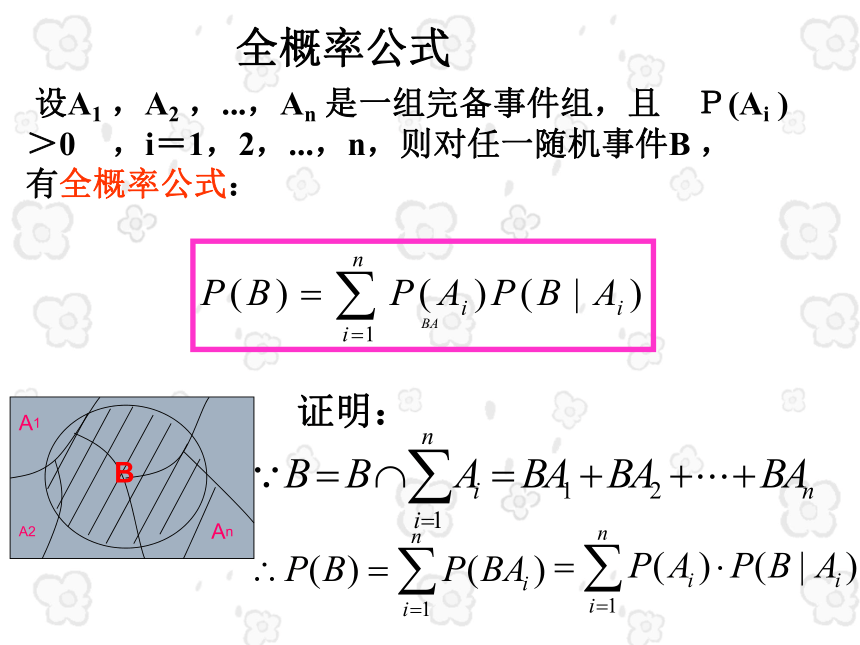
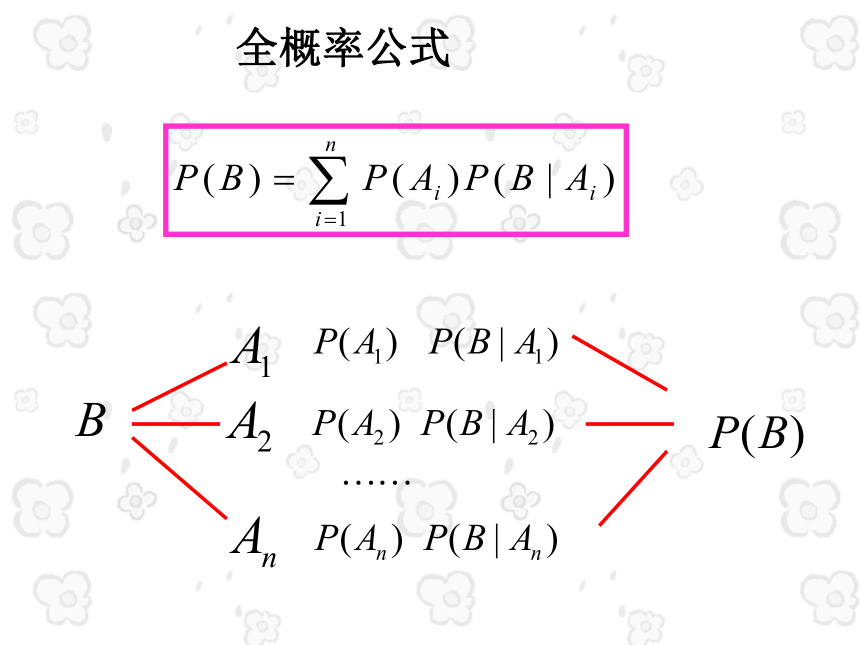
全概率公式
A1
A2
An
B
证明:
设A1 ,A2 ,...,An 是一组完备事件组,且 P(Ai )>0 ,i=1,2,...,n,则对任一随机事件B , 有全概率公式:
全概率公式
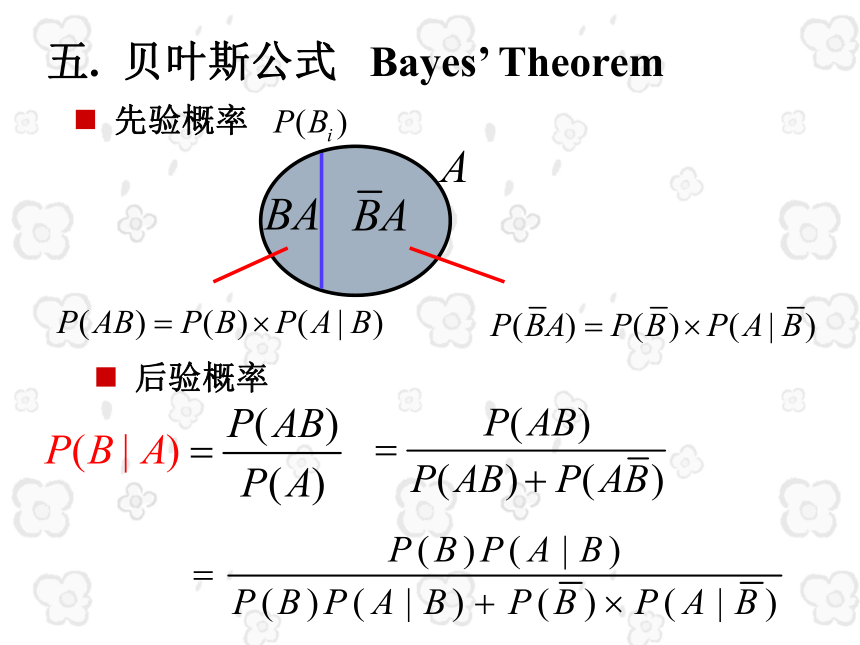
五. 贝叶斯公式 Bayes’ Theorem
后验概率
先验概率
[题型探究]
( i =1 , 2 , … , n)
证明
贝叶斯公式 Bayes’ Theorem
设B1,B2,…, Bn是一组互不相容的事件组,且诸
P(Bi)>0, 事件 ,P(A) >0 , 则有
例 有甲乙两个袋子,甲袋中有两个白球,1个红球,乙袋中有两个红球,一个白球.这六个球手感上不可区别.今从甲袋中任取一球放入乙袋,搅匀后再从乙袋中任取一球,问此球是红球的概率?
解:设A1=“从甲袋放入乙袋的是白球;
A2=“从甲袋放入乙袋的是红球”;
B=“从乙袋中任取一球是红球”;
甲
乙
思考:上例中,若已知取到一个红球,则从甲袋放入乙袋的是白球的概率是多少?
答:
A1=“从甲袋放入乙袋的是白球”;
A2=“从甲袋放入乙袋的是红球”;
B=“从乙袋中任取一球是红球”;
§7.1.2 全概率公式与贝叶斯公式
解
四、全概率公式
因为 B=AB +
,且AB与
互不相容,所以
= 0.6
一个盒子中有6只白球、4只黑球,从中不放回地每次任取1只,连取2次,求第二次取到白球的概率
例
A=“第一次取到白球” B=“第二次取到白球”
全概率公式
A1
A2
An
B
证明:
设A1 ,A2 ,...,An 是一组完备事件组,且 P(Ai )>0 ,i=1,2,...,n,则对任一随机事件B , 有全概率公式:
全概率公式
五. 贝叶斯公式 Bayes’ Theorem
后验概率
先验概率
[题型探究]
( i =1 , 2 , … , n)
证明
贝叶斯公式 Bayes’ Theorem
设B1,B2,…, Bn是一组互不相容的事件组,且诸
P(Bi)>0, 事件 ,P(A) >0 , 则有
例 有甲乙两个袋子,甲袋中有两个白球,1个红球,乙袋中有两个红球,一个白球.这六个球手感上不可区别.今从甲袋中任取一球放入乙袋,搅匀后再从乙袋中任取一球,问此球是红球的概率?
解:设A1=“从甲袋放入乙袋的是白球;
A2=“从甲袋放入乙袋的是红球”;
B=“从乙袋中任取一球是红球”;
甲
乙
思考:上例中,若已知取到一个红球,则从甲袋放入乙袋的是白球的概率是多少?
答:
A1=“从甲袋放入乙袋的是白球”;
A2=“从甲袋放入乙袋的是红球”;
B=“从乙袋中任取一球是红球”;
