.4.1 二项分布 课件 (共17张PPT) 2024-2025学年 人教A版(2019)选择性必修第三册
文档属性
| 名称 | .4.1 二项分布 课件 (共17张PPT) 2024-2025学年 人教A版(2019)选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 789.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-06 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
7.4.1 二项分布
在实际问题中,有许多试验与掷硬币试验具有相同的特征,它
们只包含两个可能的结果.如检验一件产品结果为合格或不合格,飞 碟射击时中靶或脱靶,医学检验结果为阴性或阳性等.
伯努利试验
我们把只包含两个可能结果的试验叫做伯努利试验(Bernoulli trials).
n重伯努利试验
我们将一个伯努利试验独立地重复进行n次所组成的随机试验称为n重 伯努利试验.显然,n重伯努利试验具有如下共同特征:
(1)每次试验是在同样的条件下进行的 ;
(2)各次试验中的事件是相互独立的 ;
(3)每次试验都只有两种结果:发生与不发生 ;
(4)每次试验,某事件发生的概率是相同的.
P(A1A2 … An ) = P(A1 )P(A2 )…P(An )
思考:下面3个随机试验是否为n重伯努利试验 如果是,那么其中的伯努利试验是什么 重复
试验的次数是多少?
1.抛掷一枚质地均匀的硬币10次.
2.某飞碟运动员每次射击中靶的概率为0.8 ,连续射击3次.
3.一批产品的次品率为5% ,有放回地随机抽取20件.
4.坛子中放有 3 个白球,2 个黑球,从中进行不放回地摸球。现在摸了两次球,两次 均为白球。
思考:如果连续射击4次,类比上面的分析写出中靶次数X的分布列.
中靶次数X的分布列 P(X = k) = C 0.8k × 0.24—k , k = 0, 1, 2, 3, 4.
思考:如果连续射击n次,中靶的概率为P(0P(X = k) = C pk (1— p)n—k , k = 0,1,2, … , n.
4
k
某飞碟运动员每次射击中靶的概率为0 .8, 连续3 次射击, 中靶次数X的概率的
分布列是怎样的?
P(X = k) = C 0.8k × 0.23—k , k = 0,1,2,3.
3
k
中靶次数X的概率的分布列为
二项分布
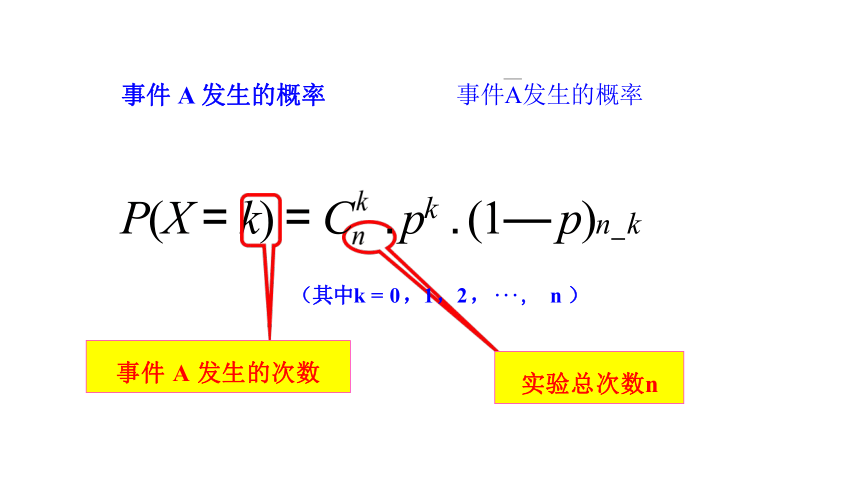
一般地,在 n 重伯努利试验中,设每次试验中事件A发生的概率p(0P(X = k) = C . pk . (1— p)n—k(其中k = 0,1,2, · · · , n)
记作X ~ B(n, p).
X 0 1 … k …
n
P C p0 q n C p1q n—1 … C pk q n—k …
C pn q0
n
n
n
1
n
0
由二项式定理, 易得 P(X = k) = C pk (1—p)n—k = [p + (1— p)]n = 1
事件 A 发生的概率 事件A发生的概率
P(X = k) = C . pk . (1— p)n k
(其中k = 0 ,1 ,2 , · · · , n )
事件 A 发生的次数
实验总次数n
例 1 将 一 枚 质地 均 匀 的 硬 币 重 复 抛 掷 1 0次 , 求
(1)恰 好 出 现 5次 正 面 朝上 的 概 率 ;
( 2 )正 面 朝 上 出 现 的 频 率 在 [0 .4 , 0 .6 ]内 的 概 率 .
解.设A="正面朝上",则P( A) = 0 .5,
用X 表示事件A发生 的次数 ,则X ~ B(10, 0 .5) .
(1)恰好 出现4次正面朝上等价于X=4,于是
P(X = 4) = C × 0 .54 × 0 .56 .
(2)正面朝上出现的频率在[0.4,0.6]内等价于4 ≤ X ≤ 6,于是
10
4
P(4 ≤ X ≤ 6) = C × 0.510 +C × 0.510 +C × 0.510 =
10
6
10
5
10
4
21
.
32
用X表示小球最后落入格子的号码,求X的分布列.
解设A=“向右下落”,则A=“向左下落”,且P(A) =P(A) =0.5.
QX等于事件A发生的次数,而小球在下落的过程中共碰撞小木钉10次, :X~B(10,0.5),于是,X的分布列为
P(X=k) =Ck10 ×0.510,k=0,1,2,L ,10.
X的概率分布列如图所示.
0 1 2 3 4 5 6 7 8 9 10
例2 如图是一块高尔顿板的示意图.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木钉,小木钉
之间留有适当的空隙作为通道,前面挡有一块玻璃,将小球从顶端放入,小球下落的过程中,每次碰到小 木钉后都等可能地向左或向右落下,最后落入底部的格子中.格子从左到右分别编号为0 ,1 ,2 , , 10,
例3.鸡接种一种疫苗后,有80%不会感染某种病毒,如果5只鸡接种了疫苗,
求(1)没有鸡感染病毒的概率; (2)恰好有1只鸡感染病毒的概率.
解.设5只接种疫苗的鸡中感染病毒的只数为X,则X ~ B (5, 0.2),
(1)P(X = 0) = C × 0.20 × 0.85 = 0.32768.
(2)P(X = 1) = C × 0.21 × 0.84 = 0.4096.
5
1
5
0
例 题
例4.甲、乙两选手进行象棋比赛,如果每局比赛甲获胜的概率为0.6,
乙获胜的概率为0.4,那么采用3局2胜制还是采用5局3胜制对甲更有利
解法1: 当采用3局2胜制时, 甲最终获胜有2种可能的比分2 : 0或2:1,
p1 = 0.62 + C × 0.62 × 0.4 = 0.648
当采用5局3胜制时,甲最终获胜的概率为
p2 = 0.63 + C × 0.63 × 0.4 + C × 0.63 × 0.42 = 0.68256
4
2
3
2
2
1
例4.甲、乙两选手进行象棋比赛,如果每局比赛甲获胜的概率为0.6,
乙获胜的概率为0.4,那么采用3局2胜制还是采用5局3胜制对甲更有利
解法2:
采月3局2胜制,不妨设赛满3局,用X表示3局比赛中甲胜的局数,则X~B3,06),
同理,5局3胜时
一般地, 如果X~B( n,p ),那么E(X)=np; D(X)=np(1-p).
证明: ∵P(X=k)= Cnkpkqn-k (∵ kCnk =n Cn- 1k-1)
:kP(X=k)= kCnkpkqn-k= npCn- 1k-1pk-1qn-k
:E (X) =0×Cn0p0qn+ 1×Cn 1p1qn-1+ 2×Cn2p2qn-2 + …+ k×Cnkpkqn-k+ …+ n×Cnnpnq0
=np(Cn-10p0qn-1+ Cn-11p1qn-2+ … + Cn-1k-1pk-1q(n-1)-(k-1) +…+ Cn-1n-1pn-1q0) =np(p+q)n-1=np
感兴趣的同学课后可尝试证明X~B( n,p )时D(X)=np(1-p).
课堂练习
3.
课堂练习
4.某人投篮的命中率为2/3,他连续投5次,求至多投中4次的概率.
5.一次英语单元测验由20个选择题构成,每个选择题有4个选项,其中有且仅有一个选 项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分。学 生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选项中随机地选择一 个。求学生甲和学生乙在这次英语单元测验中的成绩的均值。
练:一个袋子里装有大小相同的3个红球和2个黄球,从中有放回地取5次,则取到红球
次数的数学期望是 .方差是
课堂练习
6.某会议室用5盏灯照明,每盏灯各使用灯泡一只,且型号相同。假定每盏灯能否正常照明只与灯泡的寿
命有关,该型号的灯泡的寿命为1年以上的概率为 p1 ,寿命为2年以上的概率为 p 2 。从使用之日起每满1 年进行一次灯泡更换工作,只更换已坏的灯泡,平时不换。
(1)在第一次灯泡更换工作中,求不需要换灯泡的概率和更换2只灯泡的概率;
(2)在第二次灯泡更换工作中,对其中的某一盏灯来说,求该盏灯需要更换灯泡的概率;
P54-56
课外资料相应练习
超几何分布
7.4.1 二项分布
在实际问题中,有许多试验与掷硬币试验具有相同的特征,它
们只包含两个可能的结果.如检验一件产品结果为合格或不合格,飞 碟射击时中靶或脱靶,医学检验结果为阴性或阳性等.
伯努利试验
我们把只包含两个可能结果的试验叫做伯努利试验(Bernoulli trials).
n重伯努利试验
我们将一个伯努利试验独立地重复进行n次所组成的随机试验称为n重 伯努利试验.显然,n重伯努利试验具有如下共同特征:
(1)每次试验是在同样的条件下进行的 ;
(2)各次试验中的事件是相互独立的 ;
(3)每次试验都只有两种结果:发生与不发生 ;
(4)每次试验,某事件发生的概率是相同的.
P(A1A2 … An ) = P(A1 )P(A2 )…P(An )
思考:下面3个随机试验是否为n重伯努利试验 如果是,那么其中的伯努利试验是什么 重复
试验的次数是多少?
1.抛掷一枚质地均匀的硬币10次.
2.某飞碟运动员每次射击中靶的概率为0.8 ,连续射击3次.
3.一批产品的次品率为5% ,有放回地随机抽取20件.
4.坛子中放有 3 个白球,2 个黑球,从中进行不放回地摸球。现在摸了两次球,两次 均为白球。
思考:如果连续射击4次,类比上面的分析写出中靶次数X的分布列.
中靶次数X的分布列 P(X = k) = C 0.8k × 0.24—k , k = 0, 1, 2, 3, 4.
思考:如果连续射击n次,中靶的概率为P(0
4
k
某飞碟运动员每次射击中靶的概率为0 .8, 连续3 次射击, 中靶次数X的概率的
分布列是怎样的?
P(X = k) = C 0.8k × 0.23—k , k = 0,1,2,3.
3
k
中靶次数X的概率的分布列为
二项分布
一般地,在 n 重伯努利试验中,设每次试验中事件A发生的概率p(0
记作X ~ B(n, p).
X 0 1 … k …
n
P C p0 q n C p1q n—1 … C pk q n—k …
C pn q0
n
n
n
1
n
0
由二项式定理, 易得 P(X = k) = C pk (1—p)n—k = [p + (1— p)]n = 1
事件 A 发生的概率 事件A发生的概率
P(X = k) = C . pk . (1— p)n k
(其中k = 0 ,1 ,2 , · · · , n )
事件 A 发生的次数
实验总次数n
例 1 将 一 枚 质地 均 匀 的 硬 币 重 复 抛 掷 1 0次 , 求
(1)恰 好 出 现 5次 正 面 朝上 的 概 率 ;
( 2 )正 面 朝 上 出 现 的 频 率 在 [0 .4 , 0 .6 ]内 的 概 率 .
解.设A="正面朝上",则P( A) = 0 .5,
用X 表示事件A发生 的次数 ,则X ~ B(10, 0 .5) .
(1)恰好 出现4次正面朝上等价于X=4,于是
P(X = 4) = C × 0 .54 × 0 .56 .
(2)正面朝上出现的频率在[0.4,0.6]内等价于4 ≤ X ≤ 6,于是
10
4
P(4 ≤ X ≤ 6) = C × 0.510 +C × 0.510 +C × 0.510 =
10
6
10
5
10
4
21
.
32
用X表示小球最后落入格子的号码,求X的分布列.
解设A=“向右下落”,则A=“向左下落”,且P(A) =P(A) =0.5.
QX等于事件A发生的次数,而小球在下落的过程中共碰撞小木钉10次, :X~B(10,0.5),于是,X的分布列为
P(X=k) =Ck10 ×0.510,k=0,1,2,L ,10.
X的概率分布列如图所示.
0 1 2 3 4 5 6 7 8 9 10
例2 如图是一块高尔顿板的示意图.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木钉,小木钉
之间留有适当的空隙作为通道,前面挡有一块玻璃,将小球从顶端放入,小球下落的过程中,每次碰到小 木钉后都等可能地向左或向右落下,最后落入底部的格子中.格子从左到右分别编号为0 ,1 ,2 , , 10,
例3.鸡接种一种疫苗后,有80%不会感染某种病毒,如果5只鸡接种了疫苗,
求(1)没有鸡感染病毒的概率; (2)恰好有1只鸡感染病毒的概率.
解.设5只接种疫苗的鸡中感染病毒的只数为X,则X ~ B (5, 0.2),
(1)P(X = 0) = C × 0.20 × 0.85 = 0.32768.
(2)P(X = 1) = C × 0.21 × 0.84 = 0.4096.
5
1
5
0
例 题
例4.甲、乙两选手进行象棋比赛,如果每局比赛甲获胜的概率为0.6,
乙获胜的概率为0.4,那么采用3局2胜制还是采用5局3胜制对甲更有利
解法1: 当采用3局2胜制时, 甲最终获胜有2种可能的比分2 : 0或2:1,
p1 = 0.62 + C × 0.62 × 0.4 = 0.648
当采用5局3胜制时,甲最终获胜的概率为
p2 = 0.63 + C × 0.63 × 0.4 + C × 0.63 × 0.42 = 0.68256
4
2
3
2
2
1
例4.甲、乙两选手进行象棋比赛,如果每局比赛甲获胜的概率为0.6,
乙获胜的概率为0.4,那么采用3局2胜制还是采用5局3胜制对甲更有利
解法2:
采月3局2胜制,不妨设赛满3局,用X表示3局比赛中甲胜的局数,则X~B3,06),
同理,5局3胜时
一般地, 如果X~B( n,p ),那么E(X)=np; D(X)=np(1-p).
证明: ∵P(X=k)= Cnkpkqn-k (∵ kCnk =n Cn- 1k-1)
:kP(X=k)= kCnkpkqn-k= npCn- 1k-1pk-1qn-k
:E (X) =0×Cn0p0qn+ 1×Cn 1p1qn-1+ 2×Cn2p2qn-2 + …+ k×Cnkpkqn-k+ …+ n×Cnnpnq0
=np(Cn-10p0qn-1+ Cn-11p1qn-2+ … + Cn-1k-1pk-1q(n-1)-(k-1) +…+ Cn-1n-1pn-1q0) =np(p+q)n-1=np
感兴趣的同学课后可尝试证明X~B( n,p )时D(X)=np(1-p).
课堂练习
3.
课堂练习
4.某人投篮的命中率为2/3,他连续投5次,求至多投中4次的概率.
5.一次英语单元测验由20个选择题构成,每个选择题有4个选项,其中有且仅有一个选 项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分。学 生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选项中随机地选择一 个。求学生甲和学生乙在这次英语单元测验中的成绩的均值。
练:一个袋子里装有大小相同的3个红球和2个黄球,从中有放回地取5次,则取到红球
次数的数学期望是 .方差是
课堂练习
6.某会议室用5盏灯照明,每盏灯各使用灯泡一只,且型号相同。假定每盏灯能否正常照明只与灯泡的寿
命有关,该型号的灯泡的寿命为1年以上的概率为 p1 ,寿命为2年以上的概率为 p 2 。从使用之日起每满1 年进行一次灯泡更换工作,只更换已坏的灯泡,平时不换。
(1)在第一次灯泡更换工作中,求不需要换灯泡的概率和更换2只灯泡的概率;
(2)在第二次灯泡更换工作中,对其中的某一盏灯来说,求该盏灯需要更换灯泡的概率;
P54-56
课外资料相应练习
超几何分布
