7.4.2 超几何分布 课件 (共19张PPT) 2024-2025学年 人教A版(2019)选择性必修第三册
文档属性
| 名称 | 7.4.2 超几何分布 课件 (共19张PPT) 2024-2025学年 人教A版(2019)选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-06 09:38:39 | ||
图片预览






文档简介
(共19张PPT)
7.4.2 超几何分布
问题: 已知100件产品中有8件次品,分别采用有放回和不放回的方式随机抽
取4件.设抽取的4件产品中次品数为X,求随机变量X的分布列.
如果采用有放回抽样,则每次抽到次品的概率为0.08 X~B(4,0.08). 如果采用无放回抽样,那么抽到4件产品中次品数X是否服从二项分布
X不服从二项分布
X可能的取值为0,1,2,3,4, X的分布列为 k = 0,1,2,3,4.
X 0 1 2 3
4
P C C 2 C 0 C C 2 C 0 C C 2 C 0 C C 2 C 0
C C 2
C 0
10
4
9
0
8
4
10
4
9
1
8
3
10
4
9
2
8
2
10
4
9
3
8
1
10
4
9
4
8
0
超几何分布
一般地,假设一批产品共有N件,其中有M件次品.从N件产品中随机
抽取n件(不放回) ,用X表示抽取的n件产品中的次品数,则X的分布列为
P(X = k) = , k = m, m +1, m + 2, … , r.
其中n, N, M ∈ N* , M ≤ N, n ≤ N, m = max{0, n — N + M}, r = min {n, M }.
如果随机变量X的分布列具有上式的形式,那么称随机变量X 服从超几何分布.
N—总体中的个体总数
M—总体中的特殊个体总数(如次品总数)
n—样本容量
k—样本中的特殊个体数(如次品数)
例1.从50名学生中随机选出5名学生代表,求甲被选中的概率.
X服从超几何分布,且N=50,M=1,n=5, 因此甲被选中的概率为
例2.一批零件共有30个,其中有3个不合格,随机抽取10个零件进行检测, 求至少有1件不合格的概率.
解 设抽取的10个零件中不合格品数为X 则X服从超几何分布
( 13) , ( n) ( , ) ) k = 0, ,2,3.
另解: P(X ≥ 1) = 1- P ≈ 0.7192.
3
为
2
的
X
0
1
,
P
M
X
N
P
且
超几何分布的随机变量的均值与方差
得
因为 , 所以 E
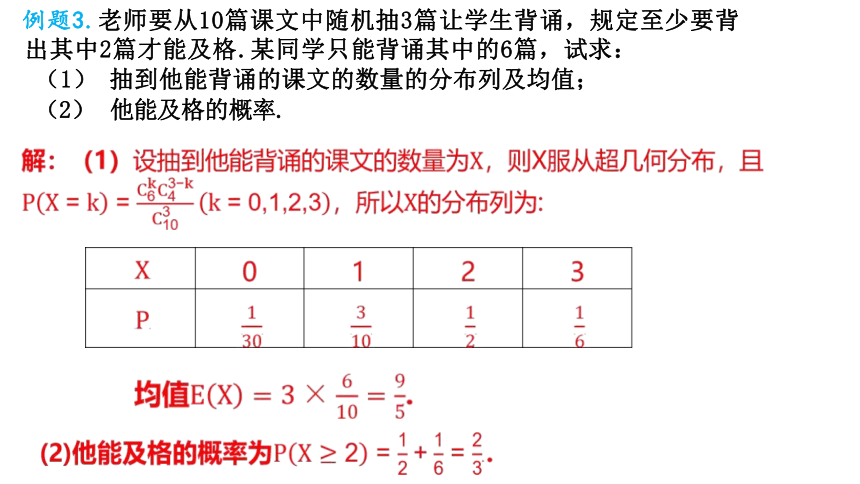
例题3.老师要从10篇课文中随机抽3篇让学生背诵,规定至少要背
出其中2篇才能及格.某同学只能背诵其中的6篇,试求:
(1) 抽到他能背诵的课文的数量的分布列及均值;
(2) 他能及格的概率.
100
例4.一袋中有100个大小相同的小球,其中有40个黄球,60个白球,从中随机摸出20个球
作为样本.用X表示样本中黄球的个数.
(1)分别就有放回和不放回摸球,求X的分布列;
(2)分别就有放回和不放回摸球,用样本中黄球的比例估计总体中黄球的比例,求误差 不超过0.1的概率.
解 (1)对于有放回摸球,由题意知x~B(20,0.4),的分布列为
P1k = P(X = k) = C2k00.4k × 0.620-k ,k = 0,1,2, …,20.
对于不放回摸球,由题意知x 服从超几何分布,X的分布列为
(2)样本中黄球的比例f20 = 是一个随机变量,根据下表计算得
有放回摸球 :
P( f20 - 0.4 ≤ 0. 1) = P(6 ≤ X ≤ 10)
≈ 0.7469.
不放回摸球 :
P( f20 - 0.4 ≤ 0. 1) = P(6 ≤ X ≤ 10)
≈ 0.7988.
采用不放回摸球估算的结果 更可靠些.
但从两种分布的概率分布图看,超几何分布更集中在均值附近.
当n远远小于N时,每次抽取一次,对N的影响很小. 此时,超几何分布可以用二项分布近似.
两种摸球方式下,随机变量X服从二项分布和超几何分布.
这两种分布的均值相等都等于8.
0.25
0.20
0.15
0.10
0.05
0
A服从二项分布
B服从超几何分布
C服从二项分布
D不服从超几何分布
课堂练习
E(X) = np =
课堂练习
:ξ的分布列为
由题ξ = 0,1,2
课堂练习
课堂练习
4.
5. 一箱24罐的饮料中4罐有奖券,每张奖券奖励饮料一罐,从中任意抽
取2罐,求这2罐中有奖券的概率.
解:设抽出的2罐中有奖券的罐数为X,则X服从超几何分布 ,从而抽取2罐 中有奖券的概率为
P(X ≥ 1) = P(X = 1)+ P(X = 2)
课本80页
探索与发现 设随机变量X ~ B(n, p)
二项分布的性质 则X的分布列为P(X = k) = C pk (1-p)n-k , k = 0 , 1 , … , n
对不同的n 和p 的值,绘制的概率分布图如图所示
记pk = P(X = k), 观察图形我们发现: 当k 由0 增大到n 时,pk 先增后减,
在某一个(或两个)k 值处达到最大. 二项分布当p = 0.5 时是对称的,
当p < 0.5 时向左偏倚, 当p > 0.5 时向右偏倚。
下面,我们利用分布列的表达式来研究pk 的增减变化及最大值
当k < (n +1)p 时,pk > pk — 1 , pk 随k 值的增加而增加;
当k > (n +1)p 时,pk < pk — 1 , pk 随k 值的增加而减小。 如果(n +1)p 为正整数, 当k = (n +1)p 时,pk = pk — 1 如果(n +1)p 为非整数,而k 取(n +1)p 的整数部分,
此时这两项概率均为最大值
则pk 是唯一的最大值
超几何分布
二项分布
试验类型 不放回 抽样
放回 抽样
试验种数 有 两 种物品
有 两 种结果
总体个数 有限 个
无限 个
随机变量取值的概率 利用古典概型 计算
利用独立重复试验计算
联系 (1)对于同一模型, 两个分布的均值相同, 但超几何分布的方差 较小, 随机变量的取值更集中于均值附件
思考:两点分布、二项分布、超几何分布有什么区别和联系?
课堂小结:
1. 超几何分布及其分布列
一般地,假设一批产品共有N件,其中有M件次品. 从N件产品中随机 抽取n件(不放回) ,用X表示抽取的n件产品中的次品数,则X的分布列为
Ck Cn—k
P(X=k) , k=m, m+1, m+2, …, r.
记为X~H(N,n,M).
2. 超几何分布的均值与方差
P57-60
课外资料相应练习 正态分布
7.4.2 超几何分布
问题: 已知100件产品中有8件次品,分别采用有放回和不放回的方式随机抽
取4件.设抽取的4件产品中次品数为X,求随机变量X的分布列.
如果采用有放回抽样,则每次抽到次品的概率为0.08 X~B(4,0.08). 如果采用无放回抽样,那么抽到4件产品中次品数X是否服从二项分布
X不服从二项分布
X可能的取值为0,1,2,3,4, X的分布列为 k = 0,1,2,3,4.
X 0 1 2 3
4
P C C 2 C 0 C C 2 C 0 C C 2 C 0 C C 2 C 0
C C 2
C 0
10
4
9
0
8
4
10
4
9
1
8
3
10
4
9
2
8
2
10
4
9
3
8
1
10
4
9
4
8
0
超几何分布
一般地,假设一批产品共有N件,其中有M件次品.从N件产品中随机
抽取n件(不放回) ,用X表示抽取的n件产品中的次品数,则X的分布列为
P(X = k) = , k = m, m +1, m + 2, … , r.
其中n, N, M ∈ N* , M ≤ N, n ≤ N, m = max{0, n — N + M}, r = min {n, M }.
如果随机变量X的分布列具有上式的形式,那么称随机变量X 服从超几何分布.
N—总体中的个体总数
M—总体中的特殊个体总数(如次品总数)
n—样本容量
k—样本中的特殊个体数(如次品数)
例1.从50名学生中随机选出5名学生代表,求甲被选中的概率.
X服从超几何分布,且N=50,M=1,n=5, 因此甲被选中的概率为
例2.一批零件共有30个,其中有3个不合格,随机抽取10个零件进行检测, 求至少有1件不合格的概率.
解 设抽取的10个零件中不合格品数为X 则X服从超几何分布
( 13) , ( n) ( , ) ) k = 0, ,2,3.
另解: P(X ≥ 1) = 1- P ≈ 0.7192.
3
为
2
的
X
0
1
,
P
M
X
N
P
且
超几何分布的随机变量的均值与方差
得
因为 , 所以 E
例题3.老师要从10篇课文中随机抽3篇让学生背诵,规定至少要背
出其中2篇才能及格.某同学只能背诵其中的6篇,试求:
(1) 抽到他能背诵的课文的数量的分布列及均值;
(2) 他能及格的概率.
100
例4.一袋中有100个大小相同的小球,其中有40个黄球,60个白球,从中随机摸出20个球
作为样本.用X表示样本中黄球的个数.
(1)分别就有放回和不放回摸球,求X的分布列;
(2)分别就有放回和不放回摸球,用样本中黄球的比例估计总体中黄球的比例,求误差 不超过0.1的概率.
解 (1)对于有放回摸球,由题意知x~B(20,0.4),的分布列为
P1k = P(X = k) = C2k00.4k × 0.620-k ,k = 0,1,2, …,20.
对于不放回摸球,由题意知x 服从超几何分布,X的分布列为
(2)样本中黄球的比例f20 = 是一个随机变量,根据下表计算得
有放回摸球 :
P( f20 - 0.4 ≤ 0. 1) = P(6 ≤ X ≤ 10)
≈ 0.7469.
不放回摸球 :
P( f20 - 0.4 ≤ 0. 1) = P(6 ≤ X ≤ 10)
≈ 0.7988.
采用不放回摸球估算的结果 更可靠些.
但从两种分布的概率分布图看,超几何分布更集中在均值附近.
当n远远小于N时,每次抽取一次,对N的影响很小. 此时,超几何分布可以用二项分布近似.
两种摸球方式下,随机变量X服从二项分布和超几何分布.
这两种分布的均值相等都等于8.
0.25
0.20
0.15
0.10
0.05
0
A服从二项分布
B服从超几何分布
C服从二项分布
D不服从超几何分布
课堂练习
E(X) = np =
课堂练习
:ξ的分布列为
由题ξ = 0,1,2
课堂练习
课堂练习
4.
5. 一箱24罐的饮料中4罐有奖券,每张奖券奖励饮料一罐,从中任意抽
取2罐,求这2罐中有奖券的概率.
解:设抽出的2罐中有奖券的罐数为X,则X服从超几何分布 ,从而抽取2罐 中有奖券的概率为
P(X ≥ 1) = P(X = 1)+ P(X = 2)
课本80页
探索与发现 设随机变量X ~ B(n, p)
二项分布的性质 则X的分布列为P(X = k) = C pk (1-p)n-k , k = 0 , 1 , … , n
对不同的n 和p 的值,绘制的概率分布图如图所示
记pk = P(X = k), 观察图形我们发现: 当k 由0 增大到n 时,pk 先增后减,
在某一个(或两个)k 值处达到最大. 二项分布当p = 0.5 时是对称的,
当p < 0.5 时向左偏倚, 当p > 0.5 时向右偏倚。
下面,我们利用分布列的表达式来研究pk 的增减变化及最大值
当k < (n +1)p 时,pk > pk — 1 , pk 随k 值的增加而增加;
当k > (n +1)p 时,pk < pk — 1 , pk 随k 值的增加而减小。 如果(n +1)p 为正整数, 当k = (n +1)p 时,pk = pk — 1 如果(n +1)p 为非整数,而k 取(n +1)p 的整数部分,
此时这两项概率均为最大值
则pk 是唯一的最大值
超几何分布
二项分布
试验类型 不放回 抽样
放回 抽样
试验种数 有 两 种物品
有 两 种结果
总体个数 有限 个
无限 个
随机变量取值的概率 利用古典概型 计算
利用独立重复试验计算
联系 (1)对于同一模型, 两个分布的均值相同, 但超几何分布的方差 较小, 随机变量的取值更集中于均值附件
思考:两点分布、二项分布、超几何分布有什么区别和联系?
课堂小结:
1. 超几何分布及其分布列
一般地,假设一批产品共有N件,其中有M件次品. 从N件产品中随机 抽取n件(不放回) ,用X表示抽取的n件产品中的次品数,则X的分布列为
Ck Cn—k
P(X=k) , k=m, m+1, m+2, …, r.
记为X~H(N,n,M).
2. 超几何分布的均值与方差
P57-60
课外资料相应练习 正态分布
