7.5 正态分布 课件 (共26张PPT)2024-2025学年 人教A版(2019)选择性必修第三册
文档属性
| 名称 | 7.5 正态分布 课件 (共26张PPT)2024-2025学年 人教A版(2019)选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-06 09:39:54 | ||
图片预览







文档简介
(共26张PPT)
7.5正态分布
高斯是一个伟大的数学家,一生中的重要贡献不胜枚举.德国的10马克纸币上印有
高斯的头像和正态分布的曲线,这就传达了一个信息:在高斯的科学贡献中,对人类文
明影响最大的是正态分布.那么,什么是正态分布?正态分布的曲线有什么特征?
如图所示是一块高尔顿板示意图.在一块木板上钉着若干排相互平行但相互错开的圆柱
形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.让一个个小球从高 尔顿板上方的通道口落下,小球在下落过程中与层层小木块碰撞,最后掉入高尔顿板下方 的某一球槽内,只有球的数目相当大,它们在底板将组成近似中间高两头低,成左右对称
的图形.
正态分布
离散型随机变量最多取可列个不同值,它等于某一特定实数的概率可
能大于0 ,离散型随机变量的概率分布规律用分布列描述,前面我们研究 的分布列(如二项分布、超几何分布等)都是离散型随机变量的分布列。
正态分布在统计学中是很重要的分布,它是一个连续型随机变量的分布,
它等于任何一个实数的概率都为0 ,所以通常感兴趣的是它落在某个区间的 概率,它的概率分布规律用密度函数(曲线)描述.
-2.6 -3.4 -0.7 -3.2 -1.7 2.9 0.6 1.7 2.9
1.2
0.5 -3.7 2.7 1.1 -3.0 -2.6 -1.9 1.7 2.6
0.4
2.6 -2.0 -0.2 1.8 -0.7 -1.3 -0.5 -1.3 0.2
-2.1
2.4 -1.5 -0.4 3.8 -0.1 1.5 0.3 -1.8 0.0
2.5
3.5 -4.2 -1.0 -0.2 0.1 0.9 1.1 2.2 0.9
-0.6
-4.4 -1.1 3.9 -1.0 -0.6 1.7 0.3 -2.4 -0.1
-1.7
-0.5 -0.8 1.7 1.4 4.4 1.2 -1.8 -3.1 -2.1
-1.6
2.2 0.3 4.8 -0.8 -3.5 -2.7 3.8 1.4 -3.5
-0.9
-2.2 -0.7 -1.3 1.5 -1.5 -2.2 1.0 1.3 1.7
-0.9
问题:自动流水线包装的食盐,每袋标准质量为400g. 由于各种不可控的因素,任 意抽取一袋食盐,它的质量与标准质量之间或多 或少会存在一定的误差(实际 质量减去标准质量). 用X表示这种误差,则X是一个连续型随机变量. 检测人员
在一次产品检验中, 随机抽取了100袋食盐,获得误差X (单位:g)的观测值如下:
-0.6 -1.4 -0.7 3.3 -2.9 -5.2 1.4 0.1 4.4 0.9
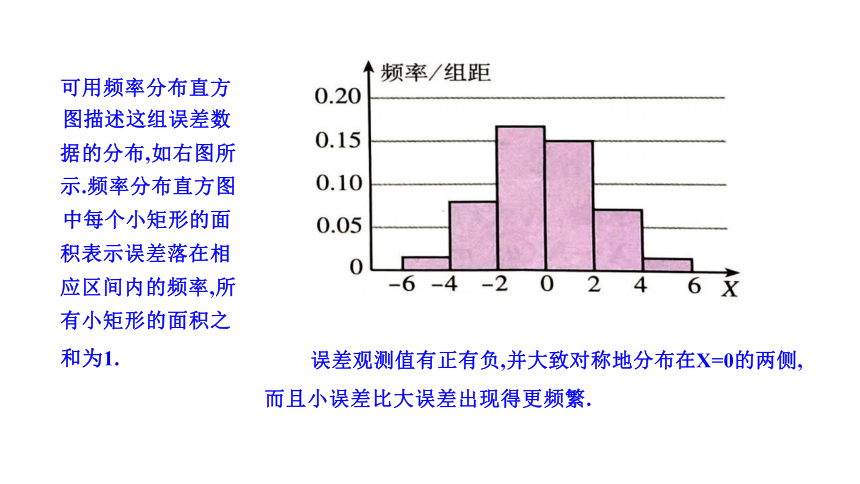
可用频率分布直方
图描述这组误差数
据的分布,如右图所
示.频率分布直方图
中每个小矩形的面
积表示误差落在相
应区间内的频率,所
有小矩形的面积之
和为1. 误差观测值有正有负,并大致对称地分布在X=0的两侧,
而且小误差比大误差出现得更频繁.
随着样本数据量越来越大,让
分组越来越多,组距越来越小, 由频 率的稳定性可知,规率分布直方图 的轮廓就越来越稳定,接近一条光 滑的钟形曲线,如右图所示。
根据频率与概率的关系,可用以用 上图中的钟型曲线来描述袋装食盐质量 误差的概率分布,曲线与水平轴之间的 面积为1.
任意抽取一袋盐,误差落在[-2,-1]内的概率如何表示
可以用图中黄色阴影部分的面积表示.
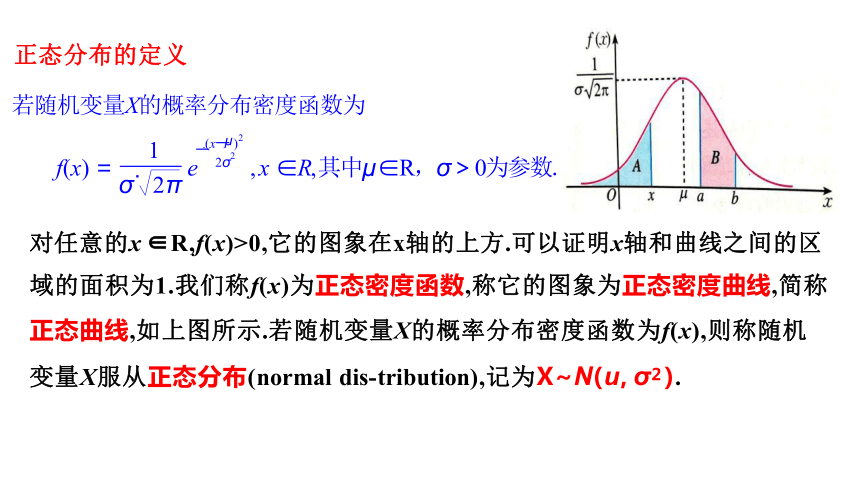
对任意的x ∈R,f(x)>0,它的图象在x轴的上方.可以证明x轴和曲线之间的区
域的面积为1.我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称 正态曲线,如上图所示.若随机变量X的概率分布密度函数为f(x),则称随机 变量X服从正态分布(normal dis-tribution),记为X~N(u, σ2 ).
正态分布的定义
若随机变量X的概率分布密度函数为
f(x) = σ· 2π e 2σ , x ∈R, 其中μ ∈R,σ > 0为参数.
1 一 (x一 )2
2
μ
若X~N(u,σ2),则如上图所示,X取值不超过x 的概率P(X)为图中区
域A的面积,而P(a≤Xy μ=0
σ= 1
0
-3 -2 -1 1 2 3 x
特别地, 当u=0, σ=1时,称随机变量X服从标准正态分布. 即X~ N(0,1).
正态曲线的性质
思考:一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线的形 状有何影响 它们反映正态分布的哪些特征
f(x) = e 2σ , x ∈ R其中μ ∈ R, σ > 0为参数.
2
-3 -2 -1 0 1 2 x -3 -2 -1 0 1 2 3 x -3 -2 -1 0 1 2 3 4x
具有两头低 、 中间高 、左右对称的基本特征
y
cμ= 1
σ=2
μ=0
σ= 1
σ=0.5
μ= -1
— (x—μ)2
y
y
μ= -1 σ=0.5 -3 -2 -1 0 1 2 x y - μ=0 σ= 1 -3 -2 -1 0 1 2 3 x
y
-3 -2 -1 0 1 2 3 4x
(1)对称性:曲线是单峰的,它关于直线x=μ对称.
(2)最值性:曲线在x=μ处达到峰值(最高点)
(3)当|x|无限增大时,曲线无限接近x轴.
当x∈(- ∞ ,μ]时,
为增函数.
当x∈[μ,+∞)时, 为减函数.
值域为 (0, ]
x ∈ R其中μ ∈ R, σ > 0为参数.
μ= 1
σ=2
y
若σ 固定, 随μ值的变化而沿x轴 平移, 故μ称为位置参数;
参数 μ , σ 的含义及对正态曲线的形状的影响
μ=0
μ= -1
参数μ反映了正态分布的集中位置,
(1). 当参数 σ取定值时,
μ1
μ=1
σ= 1
μ3
μ2
y
(2).当参数μ取定值时
: 峰值 1 与σ成反比, σ 2π
又σ > 0, 曲线与x轴
围成的面积为1.
σ越小,曲线越“瘦高 ”,表示总体的分布越集中.
若X ~ N(μ,σ 2 ), 则 E(X) = μ, D(X) = σ2
μ x
所以σ越大,曲线越“矮胖 ”,表示总体的分布越分散;
若 μ 固定,
σ大时, 曲线“矮而胖 ”; σ小时, 曲线“瘦而高 ”, 故称σ为形状参数.
μ=0
σ =0.5
σ =1
σ=2
y
正态分布的3σ原则 假设X ~ N(μ,σ2 ), 可以证明:
对给定的 k ∈ N* , P(μ一 kσ ≤ X ≤ μ +kσ)是一个只与k 有关的定值.
特别地 P(μ一σ ≤ X ≤ μ + σ) ≈ 0.6827
P(μ一 2σ ≤ X ≤ μ + 2σ) ≈ 0.9545 P(μ一 3σ ≤ X ≤ μ + 3σ) ≈ 0.9973
尽管正态变量的取值范围是( ∞,+∞),但在一次试验中,x的取值几乎
总落在区间[μ-3σ,μ+3σ]内,而在此区间外取值的概率大约只有0.0027,通常 认为这种情况几乎不可能发生.
在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量x只取 [μ-3σ,μ+3σ]中的值,这在统计学中称为3σ原则.
A
若 μ 固定,
σ大时, 曲线“矮而胖 ”; σ小时, 曲线“瘦而高 ”, 故称σ为形状参数.
D
若X ~ N(μ,σ 2 ), 则 E(X) = μ, D(X) = σ2
0.2
0.6827
5.把一个正态曲线a沿着横轴方向向右移动2个单位,得到新的一条曲线b ,下列说法
中不正确的是( D )
A. 曲线b仍然是正态曲线;
B. 曲线a和曲线b的最高点的纵坐标相等;
C. 以曲线b为概率密度曲线的总体的期望比以曲线a为概率密度曲线的总体的期望大2; D. 以曲线b为概率密度曲线的总体的方差比以曲线a为概率密度曲线的总体的方差大2。
6. 已知正态总体的数据落在(-3,-1)里的概率和落在(3,5)里的概率相等,那么这个正
态总体的数学期望是 1 。
7.如图,是一个正态曲线,试根据图象写出其正态分布的概
率密度函数的解析式,求出总体随机变量的期望和方差。
5 10 15 20 25 30 35 x
y
1
2 π
1
8.若一个正态分布的概率函数是一个偶函数且该函数的最大值等于4 · 2π ,
求该正态分布的概率密度函数的解析式。
9.某年级的一次信息技术测验成绩近似的服从正态分布 N(70, 102 ) ,如果规定低于60分
为不及格,求:
(1)成绩不及格的人数占多少?
(2)成绩在80~90内的学生占多少?
10.李明上学有时坐公交车,有时骑自行车,他各记录了50次坐公交车和骑自行车所花的时间,经数据分
析得到:坐公交车平均用时30min,样本方差为36;骑自行车平均用时34min,样本方差为4.假设坐公交车
用时X和骑自行车用时Y都服从正态分布.
(1)估计X,Y的分布中的参数 ;
(2)根据(1)中的估计结果,利用信息技术工具画出X和Y的分布密度曲线 ;
(3)如果某天有38min可用,李明应选择哪种交通工具 如果某天只有34min可用,又应该选择哪种交通工 具 请说明理由.
解:(1)随机变量X的样本均值为30,样本标准差为6;随机变量Y的样本均值为34,样本标准差为2.用样
本均值估计参数μ.用样本标准差估计参数σ ,可以得到X~N(30,62),Y~N(34,22).
(2)X和Y的分布密度曲线如图所示,
(3)应选择在给定时间内不迟到的概率大的交通工具.
由图可知,Y的密度曲线X的密度曲线P(X≤38)P(Y ≤ 34). 所以,如果有38min可用,那么骑自行车不迟到的概率大,应选择骑自行车;
如果只有34min可用,那么坐公交车不迟到的概率大,应选择坐公交车.
y A
Y的密度曲线
26 30 34 38 t
X的密度曲线
O
P61-63
课外资料相应练习
变量的相关关系
7.5正态分布
高斯是一个伟大的数学家,一生中的重要贡献不胜枚举.德国的10马克纸币上印有
高斯的头像和正态分布的曲线,这就传达了一个信息:在高斯的科学贡献中,对人类文
明影响最大的是正态分布.那么,什么是正态分布?正态分布的曲线有什么特征?
如图所示是一块高尔顿板示意图.在一块木板上钉着若干排相互平行但相互错开的圆柱
形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.让一个个小球从高 尔顿板上方的通道口落下,小球在下落过程中与层层小木块碰撞,最后掉入高尔顿板下方 的某一球槽内,只有球的数目相当大,它们在底板将组成近似中间高两头低,成左右对称
的图形.
正态分布
离散型随机变量最多取可列个不同值,它等于某一特定实数的概率可
能大于0 ,离散型随机变量的概率分布规律用分布列描述,前面我们研究 的分布列(如二项分布、超几何分布等)都是离散型随机变量的分布列。
正态分布在统计学中是很重要的分布,它是一个连续型随机变量的分布,
它等于任何一个实数的概率都为0 ,所以通常感兴趣的是它落在某个区间的 概率,它的概率分布规律用密度函数(曲线)描述.
-2.6 -3.4 -0.7 -3.2 -1.7 2.9 0.6 1.7 2.9
1.2
0.5 -3.7 2.7 1.1 -3.0 -2.6 -1.9 1.7 2.6
0.4
2.6 -2.0 -0.2 1.8 -0.7 -1.3 -0.5 -1.3 0.2
-2.1
2.4 -1.5 -0.4 3.8 -0.1 1.5 0.3 -1.8 0.0
2.5
3.5 -4.2 -1.0 -0.2 0.1 0.9 1.1 2.2 0.9
-0.6
-4.4 -1.1 3.9 -1.0 -0.6 1.7 0.3 -2.4 -0.1
-1.7
-0.5 -0.8 1.7 1.4 4.4 1.2 -1.8 -3.1 -2.1
-1.6
2.2 0.3 4.8 -0.8 -3.5 -2.7 3.8 1.4 -3.5
-0.9
-2.2 -0.7 -1.3 1.5 -1.5 -2.2 1.0 1.3 1.7
-0.9
问题:自动流水线包装的食盐,每袋标准质量为400g. 由于各种不可控的因素,任 意抽取一袋食盐,它的质量与标准质量之间或多 或少会存在一定的误差(实际 质量减去标准质量). 用X表示这种误差,则X是一个连续型随机变量. 检测人员
在一次产品检验中, 随机抽取了100袋食盐,获得误差X (单位:g)的观测值如下:
-0.6 -1.4 -0.7 3.3 -2.9 -5.2 1.4 0.1 4.4 0.9
可用频率分布直方
图描述这组误差数
据的分布,如右图所
示.频率分布直方图
中每个小矩形的面
积表示误差落在相
应区间内的频率,所
有小矩形的面积之
和为1. 误差观测值有正有负,并大致对称地分布在X=0的两侧,
而且小误差比大误差出现得更频繁.
随着样本数据量越来越大,让
分组越来越多,组距越来越小, 由频 率的稳定性可知,规率分布直方图 的轮廓就越来越稳定,接近一条光 滑的钟形曲线,如右图所示。
根据频率与概率的关系,可用以用 上图中的钟型曲线来描述袋装食盐质量 误差的概率分布,曲线与水平轴之间的 面积为1.
任意抽取一袋盐,误差落在[-2,-1]内的概率如何表示
可以用图中黄色阴影部分的面积表示.
对任意的x ∈R,f(x)>0,它的图象在x轴的上方.可以证明x轴和曲线之间的区
域的面积为1.我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称 正态曲线,如上图所示.若随机变量X的概率分布密度函数为f(x),则称随机 变量X服从正态分布(normal dis-tribution),记为X~N(u, σ2 ).
正态分布的定义
若随机变量X的概率分布密度函数为
f(x) = σ· 2π e 2σ , x ∈R, 其中μ ∈R,σ > 0为参数.
1 一 (x一 )2
2
μ
若X~N(u,σ2),则如上图所示,X取值不超过x 的概率P(X)为图中区
域A的面积,而P(a≤X
σ= 1
0
-3 -2 -1 1 2 3 x
特别地, 当u=0, σ=1时,称随机变量X服从标准正态分布. 即X~ N(0,1).
正态曲线的性质
思考:一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线的形 状有何影响 它们反映正态分布的哪些特征
f(x) = e 2σ , x ∈ R其中μ ∈ R, σ > 0为参数.
2
-3 -2 -1 0 1 2 x -3 -2 -1 0 1 2 3 x -3 -2 -1 0 1 2 3 4x
具有两头低 、 中间高 、左右对称的基本特征
y
cμ= 1
σ=2
μ=0
σ= 1
σ=0.5
μ= -1
— (x—μ)2
y
y
μ= -1 σ=0.5 -3 -2 -1 0 1 2 x y - μ=0 σ= 1 -3 -2 -1 0 1 2 3 x
y
-3 -2 -1 0 1 2 3 4x
(1)对称性:曲线是单峰的,它关于直线x=μ对称.
(2)最值性:曲线在x=μ处达到峰值(最高点)
(3)当|x|无限增大时,曲线无限接近x轴.
当x∈(- ∞ ,μ]时,
为增函数.
当x∈[μ,+∞)时, 为减函数.
值域为 (0, ]
x ∈ R其中μ ∈ R, σ > 0为参数.
μ= 1
σ=2
y
若σ 固定, 随μ值的变化而沿x轴 平移, 故μ称为位置参数;
参数 μ , σ 的含义及对正态曲线的形状的影响
μ=0
μ= -1
参数μ反映了正态分布的集中位置,
(1). 当参数 σ取定值时,
μ1
μ=1
σ= 1
μ3
μ2
y
(2).当参数μ取定值时
: 峰值 1 与σ成反比, σ 2π
又σ > 0, 曲线与x轴
围成的面积为1.
σ越小,曲线越“瘦高 ”,表示总体的分布越集中.
若X ~ N(μ,σ 2 ), 则 E(X) = μ, D(X) = σ2
μ x
所以σ越大,曲线越“矮胖 ”,表示总体的分布越分散;
若 μ 固定,
σ大时, 曲线“矮而胖 ”; σ小时, 曲线“瘦而高 ”, 故称σ为形状参数.
μ=0
σ =0.5
σ =1
σ=2
y
正态分布的3σ原则 假设X ~ N(μ,σ2 ), 可以证明:
对给定的 k ∈ N* , P(μ一 kσ ≤ X ≤ μ +kσ)是一个只与k 有关的定值.
特别地 P(μ一σ ≤ X ≤ μ + σ) ≈ 0.6827
P(μ一 2σ ≤ X ≤ μ + 2σ) ≈ 0.9545 P(μ一 3σ ≤ X ≤ μ + 3σ) ≈ 0.9973
尽管正态变量的取值范围是( ∞,+∞),但在一次试验中,x的取值几乎
总落在区间[μ-3σ,μ+3σ]内,而在此区间外取值的概率大约只有0.0027,通常 认为这种情况几乎不可能发生.
在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量x只取 [μ-3σ,μ+3σ]中的值,这在统计学中称为3σ原则.
A
若 μ 固定,
σ大时, 曲线“矮而胖 ”; σ小时, 曲线“瘦而高 ”, 故称σ为形状参数.
D
若X ~ N(μ,σ 2 ), 则 E(X) = μ, D(X) = σ2
0.2
0.6827
5.把一个正态曲线a沿着横轴方向向右移动2个单位,得到新的一条曲线b ,下列说法
中不正确的是( D )
A. 曲线b仍然是正态曲线;
B. 曲线a和曲线b的最高点的纵坐标相等;
C. 以曲线b为概率密度曲线的总体的期望比以曲线a为概率密度曲线的总体的期望大2; D. 以曲线b为概率密度曲线的总体的方差比以曲线a为概率密度曲线的总体的方差大2。
6. 已知正态总体的数据落在(-3,-1)里的概率和落在(3,5)里的概率相等,那么这个正
态总体的数学期望是 1 。
7.如图,是一个正态曲线,试根据图象写出其正态分布的概
率密度函数的解析式,求出总体随机变量的期望和方差。
5 10 15 20 25 30 35 x
y
1
2 π
1
8.若一个正态分布的概率函数是一个偶函数且该函数的最大值等于4 · 2π ,
求该正态分布的概率密度函数的解析式。
9.某年级的一次信息技术测验成绩近似的服从正态分布 N(70, 102 ) ,如果规定低于60分
为不及格,求:
(1)成绩不及格的人数占多少?
(2)成绩在80~90内的学生占多少?
10.李明上学有时坐公交车,有时骑自行车,他各记录了50次坐公交车和骑自行车所花的时间,经数据分
析得到:坐公交车平均用时30min,样本方差为36;骑自行车平均用时34min,样本方差为4.假设坐公交车
用时X和骑自行车用时Y都服从正态分布.
(1)估计X,Y的分布中的参数 ;
(2)根据(1)中的估计结果,利用信息技术工具画出X和Y的分布密度曲线 ;
(3)如果某天有38min可用,李明应选择哪种交通工具 如果某天只有34min可用,又应该选择哪种交通工 具 请说明理由.
解:(1)随机变量X的样本均值为30,样本标准差为6;随机变量Y的样本均值为34,样本标准差为2.用样
本均值估计参数μ.用样本标准差估计参数σ ,可以得到X~N(30,62),Y~N(34,22).
(2)X和Y的分布密度曲线如图所示,
(3)应选择在给定时间内不迟到的概率大的交通工具.
由图可知,Y的密度曲线X的密度曲线P(X≤38)
如果只有34min可用,那么坐公交车不迟到的概率大,应选择坐公交车.
y A
Y的密度曲线
26 30 34 38 t
X的密度曲线
O
P61-63
课外资料相应练习
变量的相关关系
