人教A版(2019)选择性必修第三册 8.1.2 样本相关系数 课件(共22张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第三册 8.1.2 样本相关系数 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 948.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-06 14:14:09 | ||
图片预览







文档简介
(共22张PPT)
8.1.2 样本相关系数
通过观察散点图中成对样本数据的分布规律,我们可以大致推断两个变
量是否存在相关关系、是正相关还是负相关、是线性相关还是非线性相关
等. 散点图虽然直观,但无法确切地反映成对样本数据的相关程度,也就 无法量化两个变量之间相关程度的大小. 能否像引人均值、方差等数字特 征对单个变量数据进行分析那样,引入一个适当的“数字特征” ,对成对样 本数据的相关程度进行定量分析呢
对于变量x和变量y ,设经过随机抽样获得的成对样本数据为(x1, y1), (x2,
y2), , (xn, yn) ,其中x1, x2, , xn和y1, y2, , yn 的均值分别为 x和y . 将数据
以(x,y) 为零点进行平移,得到平移后的成对数据为
(x1 — x,y1 — y ),(x2 — x,y2 — y ),. ..,(xn — x,yn — y ), 并绘制散点图.
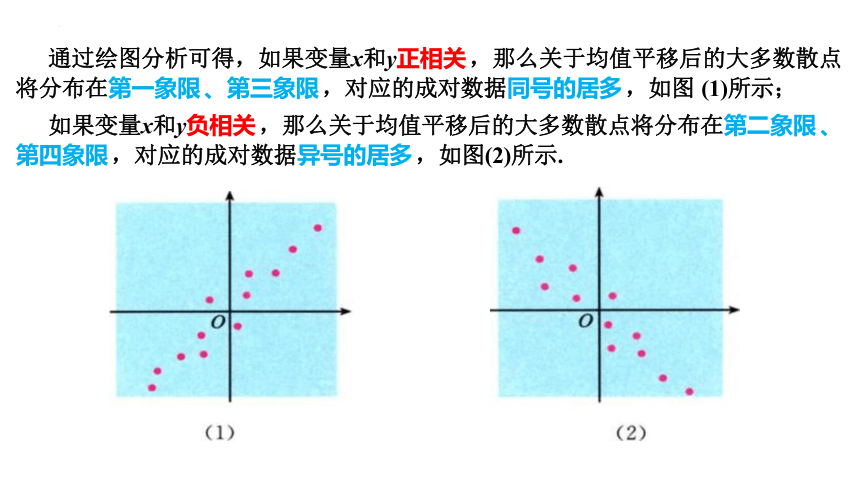
通过绘图分析可得,如果变量x和y正相关 ,那么关于均值平移后的大多数散点 将分布在第一象限 、第三象限 ,对应的成对数据同号的居多 ,如图 (1)所示;
如果变量x和y负相关 ,那么关于均值平移后的大多数散点将分布在第二象限 、 第四象限 ,对应的成对数据异号的居多 ,如图(2)所示.
思考1 根据上述分析,你能利用正相关变量和负相关变量的成对样本数据
平移后呈现的规律,构造一个度量成对样本数据是正相关还是负相关的数
字特征吗
利用散点(xi — x,yi — y )(i = 1, 2, . . ., n) 的横 、纵坐标是否同号 ,可以构造 一个量
= [(x1 — x )(y1 — y ) + (x2 — x )(y2 — y ) + . . . + (xn — x )(yn — y )].
一般情形下,Lxy>0表明成对样本数据正相关; Lxy <0表明成对样本数据负相关.
L
xy
思考2 Lxy的大小是否一定能度量出成对样本数据的相关程度吗
因为Lxy的大小与数据的度量单位有关,所以不宜直接用它度量成对样本数据相关 程度的大小. 为了消除度量单位的影响,需要对数据作进一步的“标准化”处理. 我们用
分别除xi — x和yi — y (i = 1, 2, . . ., n),并仿照Lxy的构造可得
我们称r为变量x和变量y的样本相关系数.
(xi — x)(yi — y)
r =
· (xi — x)2 . · (yi — y)2
+…+ 同理可得
2
思考3 样本相关系数r的大小与成对样本数据的相关程度有什么内在联系呢?
标准化处理后的成对样本数据: (x1' , y1'), (x2 ' , y2 '), ..., (xn' , yn')
-→ -
设其第一分量为 x' = (x1' , x2 ' , ..., xn ' ) 设其第二分量为 y' = (y1' , y2' , ..., yn' )
● | cos θ r = cosθ :-1≤ r ≤1
相关系数的性质:
① 当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关.
② |r|≤1;
③ 当|r|越接近1时,成对数据的线性相关程度越强;当|r|越接近0时,成对数 据的线性相关程度越弱;注意,当|r| =0时,成对数据没有线性相关关系,但不 排除它们之间有其他相关关系;当|r| =1时,成对数据都落在一条直线上.
一般地:若0.75≤|r|≤1 , 则认为y与x的线性相关程度很强;
若0.3 ≤|r|<0.75 , 则认为y与x的线性相关程度一般;
若|r|≤0.25 , 则认为y与x的线性相关程度较弱.
样本相关系数
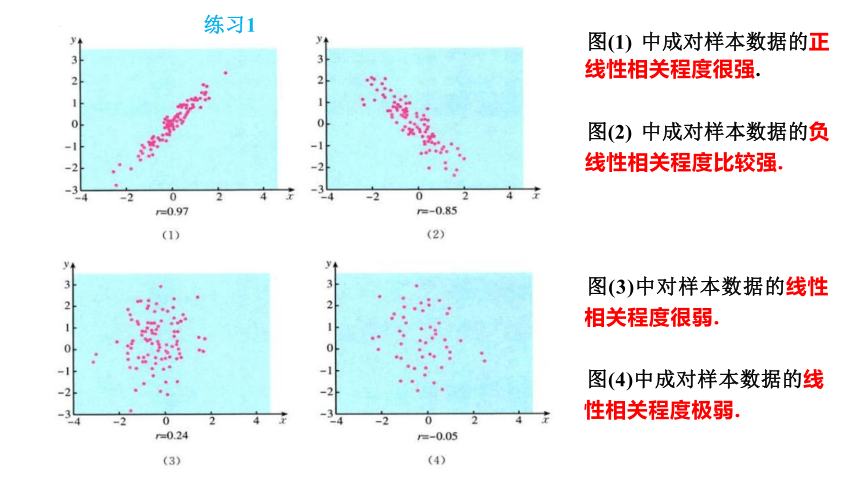
图(1) 中成对样本数据的正 线性相关程度很强.
图(2) 中成对样本数据的负
线性相关程度比较强.
图(3)中对样本数据的线性
相关程度很弱.
图(4)中成对样本数据的线
性相关程度极弱.
练习1
√
练习3.两个变量x ,y的样本相关系数r1 =0.7859 ,两个变量u ,v的样本相关系数r2
= -0.9568 ,则下列判断正确的是( C )
A.变量x与y正相关,变量u与v负相关,变量x与y的线性相关性较强 B.变量x与y负相关,变量u与v正相关,变量x与y的线性相关性较强 C.变量x与y正相关,变量u与v负相关,变量u与v 的线性相关性较强 D.变量x与y负相关,变量u与v正相关,变量u与v 的线性相关性较强
8.对四组数据进行统计,获得以下散点图,关于其样本相关系数的比较
, 正确的是( A )
A.r2练习1 判断正误(正确的打“√” , 错误的打“×”)
(1)相关关系是一种非确定性关系,体现的不一定是因果关系
系.( √ )
(2)散点图越接近某一条直线,线性相关程度越强,样本相关
(3)散点图可以直观地分析出两个变量是否具有相关性.(√
(4)若变量x,y满足函数关系,则这两个变量线性相关.( ×
练习2 已知求得甲、乙、丙3组不同的数据的样本相关系数分别为0.81 ,-0.98,
0.63 ,其中 乙 (填甲、乙或丙)组数据的线性相关程度最强.
, 可能是伴随关
系数越大.( ×)
) )
解: 由样本数据可得 x ≈ 48.07,y ≈ 27.26, (xi — x )(yi — y ) ≈ 1054.34,
≈ 0.97.
由此可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13
14
年龄/岁 23 27 39 41 45 49 50 53 54 56 57 58 60
61
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2 29.6 30.2 31.4 30.8 33.5 35.2
34.6
例1 根据表8. 1-1中脂肪含量和年龄的样本数据,推断两个变量是否线性相
关,计算样本相关系数,并推断它们的相关程度.
解: 由样本数据可得
编号 1 2 3 4 5 6 7 8 9 10 11 12 13
14
年龄/岁 23 27 39 41 45 49 50 53 54 56 57 58 60
61
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2 29.6 30.2 31.4 30.8 33.5 35.2
34.6
例1 根据表8. 1-1中脂肪含量和年龄的样本数据,推断两个变量是否线性相
关,计算样本相关系数,并推断它们的相关程度.
xi yi — 14xy
·i x — 14x . y — 14y
2
2
i
2
i
2
(xi — x)(yi — y)
·i (xi — x) . ·i (yi — y)
2
2
由此可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强.
∴r =
≈ 0.97.
=
练习1 在一次试验中,测得(x, y)的4组值分别为(1, 2), (2, 0), (4, -4), (-1,6), 则y与x的样本相关系数为( )
A .1 B .-2 C .0 √D.-1
解:由样本数据可得 xi yi = —20, = 22, = 56.
xi yi — 4xy 20 4 × 3 × 1
∴r = i =1 = 2 = 1.
x — 4x2 . y — 4y2 22 — 4× ( )2 × 56 — 4× 12
2
3
i
2
i
2
根据上表数据, 计算y与x的样本相关系数r, 并说明y与x的线性相关程度.
(附: 若0.75≤|r|≤1 ,则认为y与x的线性相关程度很强;若0.3≤|r|<0.75 ,则认为 y与x的线性相关程度一般;|r|≤0.25 ,则认为y与x的线性相关程度较弱)
年份x 2016 2017 2018 2019
2020
足球特色学校y(百个) 0.30 0.60 1.00 1.40
1.70
练习2 足球是深受全世界人们喜爱的运动,我国大力发展校园足球.为
了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
参考公式和数据
(xi — x)2 = 10, (yi — y)2 = 1.3,· i13 ≈ 3.6056.
请推断超市的销售额与广告支出之间的相关关系的类型、相关程度和变
化趋势的特征.
解:由样本数据可得 = 42, xi yi = 2841, = 753, = 13350.
超市 A B C D E F
G
广告支出x/万元 1 2 4 6 10 14
20
销售额y/万元 19 32 44 40 52 53
54
xi yi — 7xy 2841 7 ×
∴r = i =1 =
x — 7x2 . y — 7y2 753 — 7 × ( )2 × 13350 — 7 × 422
7
57
i
2
i
2
课本103页
练习3. 随机抽取7家超市,得到其广告支出与销售额数据如下:
正线性相关,相关性较强,销售额与广告支出的变化趋势相同.
× 42
≈ 0.83.
57
7
课本103页
练习4. 已知变量x和变量y的3对随机观测数据(2, 2), (3, -1), (5, -7) ,计算
成对样本数据的样本相关系数. 能据此推断这两个变量线性相关吗 为什么
解:由样本数据可得 = —2, xi yi = 2 × 2 + 3× = —34,
2 = — 1.
虽然样本相关系数为-1 ,三个样本点在一条直线上,但是由于样本 量太小 ,据此推断两个变量完全线性相关并不可靠.
y
3 4 x
相关系数在刻画成对样本数据相关关系上的特点.
(1) (-2, -3), (-1, -1), (0, 1), (1, 3), (2, 5), (3, 7);
(2) (0, 0), (1, 1), (2, 4), (3, 9), (4, 16);
(3) (-2, -8), (-1, -1), (0, 0), (1, 1), (2, 8), (3, 27);
(4) (2, 0) (1, · 3 ), (0, 2), (-1, · 3 ), (-2, 0).
y r = 0.89 25 - 20 - 15 - 10 - 5 - - 0 1 -5 - -10 - 2 3
x
解: -3 -2 r = 1 8 - 6 - 4 - 2 - - 0 - 1 2 -2 -4 -
3 x
-3 -2 y 2 1.5 - 1 - 0.5 - -1 0 1
r = 0
2 3 x
课本103页
练习5. 画出下列成对数据的散点图,并计算样本相关系数. 据此,请你谈谈样本
样本相关系数主要刻画的是成对样本数据线性相关的程度.
15 -
10 - 5 -
0
-3 -2
r = 0.96
1 2
y
课堂小结:
1. 样本相关系数
2.相关系数的性质:
① 当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关.
② |r|≤1;
③ 当|r|越接近1时,成对数据的线性相关程度越强;当|r|越接近0时,成对数 据的线性相关程度越弱;特别地,当|r| =0时,成对数据的没有线性相关关系; 当|r| =1时,成对数据都落在一条直线上.
P67-71
课外资料相应练习
一元线性回归模型及其应用( 1)
/
8.1.2 样本相关系数
通过观察散点图中成对样本数据的分布规律,我们可以大致推断两个变
量是否存在相关关系、是正相关还是负相关、是线性相关还是非线性相关
等. 散点图虽然直观,但无法确切地反映成对样本数据的相关程度,也就 无法量化两个变量之间相关程度的大小. 能否像引人均值、方差等数字特 征对单个变量数据进行分析那样,引入一个适当的“数字特征” ,对成对样 本数据的相关程度进行定量分析呢
对于变量x和变量y ,设经过随机抽样获得的成对样本数据为(x1, y1), (x2,
y2), , (xn, yn) ,其中x1, x2, , xn和y1, y2, , yn 的均值分别为 x和y . 将数据
以(x,y) 为零点进行平移,得到平移后的成对数据为
(x1 — x,y1 — y ),(x2 — x,y2 — y ),. ..,(xn — x,yn — y ), 并绘制散点图.
通过绘图分析可得,如果变量x和y正相关 ,那么关于均值平移后的大多数散点 将分布在第一象限 、第三象限 ,对应的成对数据同号的居多 ,如图 (1)所示;
如果变量x和y负相关 ,那么关于均值平移后的大多数散点将分布在第二象限 、 第四象限 ,对应的成对数据异号的居多 ,如图(2)所示.
思考1 根据上述分析,你能利用正相关变量和负相关变量的成对样本数据
平移后呈现的规律,构造一个度量成对样本数据是正相关还是负相关的数
字特征吗
利用散点(xi — x,yi — y )(i = 1, 2, . . ., n) 的横 、纵坐标是否同号 ,可以构造 一个量
= [(x1 — x )(y1 — y ) + (x2 — x )(y2 — y ) + . . . + (xn — x )(yn — y )].
一般情形下,Lxy>0表明成对样本数据正相关; Lxy <0表明成对样本数据负相关.
L
xy
思考2 Lxy的大小是否一定能度量出成对样本数据的相关程度吗
因为Lxy的大小与数据的度量单位有关,所以不宜直接用它度量成对样本数据相关 程度的大小. 为了消除度量单位的影响,需要对数据作进一步的“标准化”处理. 我们用
分别除xi — x和yi — y (i = 1, 2, . . ., n),并仿照Lxy的构造可得
我们称r为变量x和变量y的样本相关系数.
(xi — x)(yi — y)
r =
· (xi — x)2 . · (yi — y)2
+…+ 同理可得
2
思考3 样本相关系数r的大小与成对样本数据的相关程度有什么内在联系呢?
标准化处理后的成对样本数据: (x1' , y1'), (x2 ' , y2 '), ..., (xn' , yn')
-→ -
设其第一分量为 x' = (x1' , x2 ' , ..., xn ' ) 设其第二分量为 y' = (y1' , y2' , ..., yn' )
● | cos θ r = cosθ :-1≤ r ≤1
相关系数的性质:
① 当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关.
② |r|≤1;
③ 当|r|越接近1时,成对数据的线性相关程度越强;当|r|越接近0时,成对数 据的线性相关程度越弱;注意,当|r| =0时,成对数据没有线性相关关系,但不 排除它们之间有其他相关关系;当|r| =1时,成对数据都落在一条直线上.
一般地:若0.75≤|r|≤1 , 则认为y与x的线性相关程度很强;
若0.3 ≤|r|<0.75 , 则认为y与x的线性相关程度一般;
若|r|≤0.25 , 则认为y与x的线性相关程度较弱.
样本相关系数
图(1) 中成对样本数据的正 线性相关程度很强.
图(2) 中成对样本数据的负
线性相关程度比较强.
图(3)中对样本数据的线性
相关程度很弱.
图(4)中成对样本数据的线
性相关程度极弱.
练习1
√
练习3.两个变量x ,y的样本相关系数r1 =0.7859 ,两个变量u ,v的样本相关系数r2
= -0.9568 ,则下列判断正确的是( C )
A.变量x与y正相关,变量u与v负相关,变量x与y的线性相关性较强 B.变量x与y负相关,变量u与v正相关,变量x与y的线性相关性较强 C.变量x与y正相关,变量u与v负相关,变量u与v 的线性相关性较强 D.变量x与y负相关,变量u与v正相关,变量u与v 的线性相关性较强
8.对四组数据进行统计,获得以下散点图,关于其样本相关系数的比较
, 正确的是( A )
A.r2
(1)相关关系是一种非确定性关系,体现的不一定是因果关系
系.( √ )
(2)散点图越接近某一条直线,线性相关程度越强,样本相关
(3)散点图可以直观地分析出两个变量是否具有相关性.(√
(4)若变量x,y满足函数关系,则这两个变量线性相关.( ×
练习2 已知求得甲、乙、丙3组不同的数据的样本相关系数分别为0.81 ,-0.98,
0.63 ,其中 乙 (填甲、乙或丙)组数据的线性相关程度最强.
, 可能是伴随关
系数越大.( ×)
) )
解: 由样本数据可得 x ≈ 48.07,y ≈ 27.26, (xi — x )(yi — y ) ≈ 1054.34,
≈ 0.97.
由此可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13
14
年龄/岁 23 27 39 41 45 49 50 53 54 56 57 58 60
61
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2 29.6 30.2 31.4 30.8 33.5 35.2
34.6
例1 根据表8. 1-1中脂肪含量和年龄的样本数据,推断两个变量是否线性相
关,计算样本相关系数,并推断它们的相关程度.
解: 由样本数据可得
编号 1 2 3 4 5 6 7 8 9 10 11 12 13
14
年龄/岁 23 27 39 41 45 49 50 53 54 56 57 58 60
61
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2 29.6 30.2 31.4 30.8 33.5 35.2
34.6
例1 根据表8. 1-1中脂肪含量和年龄的样本数据,推断两个变量是否线性相
关,计算样本相关系数,并推断它们的相关程度.
xi yi — 14xy
·i x — 14x . y — 14y
2
2
i
2
i
2
(xi — x)(yi — y)
·i (xi — x) . ·i (yi — y)
2
2
由此可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强.
∴r =
≈ 0.97.
=
练习1 在一次试验中,测得(x, y)的4组值分别为(1, 2), (2, 0), (4, -4), (-1,6), 则y与x的样本相关系数为( )
A .1 B .-2 C .0 √D.-1
解:由样本数据可得 xi yi = —20, = 22, = 56.
xi yi — 4xy 20 4 × 3 × 1
∴r = i =1 = 2 = 1.
x — 4x2 . y — 4y2 22 — 4× ( )2 × 56 — 4× 12
2
3
i
2
i
2
根据上表数据, 计算y与x的样本相关系数r, 并说明y与x的线性相关程度.
(附: 若0.75≤|r|≤1 ,则认为y与x的线性相关程度很强;若0.3≤|r|<0.75 ,则认为 y与x的线性相关程度一般;|r|≤0.25 ,则认为y与x的线性相关程度较弱)
年份x 2016 2017 2018 2019
2020
足球特色学校y(百个) 0.30 0.60 1.00 1.40
1.70
练习2 足球是深受全世界人们喜爱的运动,我国大力发展校园足球.为
了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
参考公式和数据
(xi — x)2 = 10, (yi — y)2 = 1.3,· i13 ≈ 3.6056.
请推断超市的销售额与广告支出之间的相关关系的类型、相关程度和变
化趋势的特征.
解:由样本数据可得 = 42, xi yi = 2841, = 753, = 13350.
超市 A B C D E F
G
广告支出x/万元 1 2 4 6 10 14
20
销售额y/万元 19 32 44 40 52 53
54
xi yi — 7xy 2841 7 ×
∴r = i =1 =
x — 7x2 . y — 7y2 753 — 7 × ( )2 × 13350 — 7 × 422
7
57
i
2
i
2
课本103页
练习3. 随机抽取7家超市,得到其广告支出与销售额数据如下:
正线性相关,相关性较强,销售额与广告支出的变化趋势相同.
× 42
≈ 0.83.
57
7
课本103页
练习4. 已知变量x和变量y的3对随机观测数据(2, 2), (3, -1), (5, -7) ,计算
成对样本数据的样本相关系数. 能据此推断这两个变量线性相关吗 为什么
解:由样本数据可得 = —2, xi yi = 2 × 2 + 3× = —34,
2 = — 1.
虽然样本相关系数为-1 ,三个样本点在一条直线上,但是由于样本 量太小 ,据此推断两个变量完全线性相关并不可靠.
y
3 4 x
相关系数在刻画成对样本数据相关关系上的特点.
(1) (-2, -3), (-1, -1), (0, 1), (1, 3), (2, 5), (3, 7);
(2) (0, 0), (1, 1), (2, 4), (3, 9), (4, 16);
(3) (-2, -8), (-1, -1), (0, 0), (1, 1), (2, 8), (3, 27);
(4) (2, 0) (1, · 3 ), (0, 2), (-1, · 3 ), (-2, 0).
y r = 0.89 25 - 20 - 15 - 10 - 5 - - 0 1 -5 - -10 - 2 3
x
解: -3 -2 r = 1 8 - 6 - 4 - 2 - - 0 - 1 2 -2 -4 -
3 x
-3 -2 y 2 1.5 - 1 - 0.5 - -1 0 1
r = 0
2 3 x
课本103页
练习5. 画出下列成对数据的散点图,并计算样本相关系数. 据此,请你谈谈样本
样本相关系数主要刻画的是成对样本数据线性相关的程度.
15 -
10 - 5 -
0
-3 -2
r = 0.96
1 2
y
课堂小结:
1. 样本相关系数
2.相关系数的性质:
① 当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关.
② |r|≤1;
③ 当|r|越接近1时,成对数据的线性相关程度越强;当|r|越接近0时,成对数 据的线性相关程度越弱;特别地,当|r| =0时,成对数据的没有线性相关关系; 当|r| =1时,成对数据都落在一条直线上.
P67-71
课外资料相应练习
一元线性回归模型及其应用( 1)
/
