8.3 列联表与独立性检验 课件 (共19张PPT)2024-2025学年 人教A版(2019)选择性必修第三册
文档属性
| 名称 | 8.3 列联表与独立性检验 课件 (共19张PPT)2024-2025学年 人教A版(2019)选择性必修第三册 |  | |
| 格式 | pptx | ||
| 文件大小 | 812.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-06 09:37:49 | ||
图片预览






文档简介
(共19张PPT)
8.3列联表与独立性检验
1.分类变量
在现实生活中,人们经常需要回答一定范围内的两种现象或性质之间 是否存在关联性或互相影响的问题.
例如:就读不同学校是否对学生的成绩有影响,不同班级学生用于
体育锻炼的时间是否存在区别,吸烟是否会增加患肺癌的风险等。
在讨论上述问题时 , 为了表述方便 , 我们经常会使用一种特殊的随机变量 , 以区别 不同的现象或性质 , 这类随机变量称为分类变量.
分类变量:用实数表示不同的现象或性质.
如:班级:1、2、3, 男生、女生:0、1.
本节主要讨论取值于{0,1}的分类变量的关联性
问题1:为了有针对性地提高学生体育锻炼的积极性,某中学需要了解性别因素是否对本
校学生体育锻炼的经常性有影响,为此对学生是否经常锻炼的情况进行了普查.全校生 的普查数据如下:523名女生中有331名经常锻炼,601名男生中有473名经常锻炼.你能利 用这些数据,说明该校女生和男生在体育锻炼的经常性方面是否存在差异吗
解1:比较经常锻炼的学生在女生和男中的比率.
f0 = 经常 生数,f1 = 经常 生数.
≈ 0.633,f1 = ≈ 0.787. f1 0 = 0.787-0.633=0. 154.
男生经常锻炼的比率比女生高出15.4个百分点,所以该校的女生和男生在体育锻 炼的经常性方面有差异,而且男生更经常锻炼.
男生总数
锻炼的男
女生总数
锻炼的女
若性别对体育锻炼的经常性没有影响,可描述为 P (Y = 1 X = 0) = P(Y = 1 X = 1)
若性别对体育锻炼的经常性有影响,可描述为 P (Y = 1 X = 0) ≠ P(Y = 1 X = 1)
性别 锻炼
合计
不经常(Y =0) 经常(Y =1) 女生(X =0) 192 331
523
男生(X =1) 128 473
601
合计 320 804
1124
P(Y = 1X = 1)>P(Y = 1X = 0)
[0,该生不经常锻炼,
Y = {
0,该生为女生,
1,该生为男生,,
解2: 对于Ω中的每一名学生,分别令
∴性别对体育锻炼的经常性有影响
l1 ,该生经常锻炼,
[
X = {
l
X Y
合计
Y =0 Y=1 X =0 a b
a+b
X=1 c d
c+d
合计 a+c b +d
n =a+b +c+d
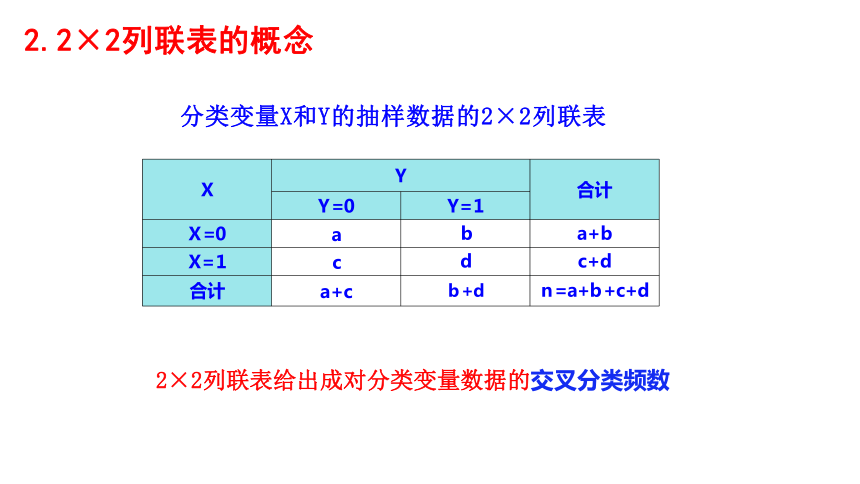
2.2×2列联表的概念
分类变量X和Y的抽样数据的2×2列联表
2×2列联表给出成对分类变量数据的交叉分类频数
例1.为比较甲、乙两所学校学生的数学水平,采用简单随机抽样的方法抽取88名学生.
通过测验得到了如下数据:甲校43名学生中有10名数学成绩优秀;乙校45名学生中有7名 数学成绩优秀.试分析两校学生中数学成绩优秀率之间是否存在差异.
解:用Ω表示两所学校的全体学生构成的集合.考虑以Ω为样本空间的古典概型.对 于Ω中每一名学生,定义分类变量X和Y如下:
因此,甲校学生中数学成绩不优秀和数学成绩优秀的频率分别为 ≈ 0.7674, ≈ 0.2326.
乙校学生中数学成绩不优秀和数学成绩优秀的频率分别为 ≈ 0.8444, ≈ 0. 1556.
学校 数学成绩
合计
不优秀 Y= 优 = 甲校 (
乙校(X 1) 38 7
合计 71 17
[0, 该生数学成绩不优秀,
Y = {
0, 该生来 自 甲校,
1,该生来 自 乙校,,
l 1 ,该生数学成绩优秀,
[
X = {
l
两个分类变量之间关联关系的定性分析的方法:
(1)频率分析法:通过对样本的每个分类变量的不同类别事件发生的频 率大小进行比较来分析分类变量之间是否有关联关系.
(2)图形分析法:与表格相比,图形更能直观地反映出两个分类变量间是 否互相影响,常用等高堆积条形图展示列联表数据的频率特征.
你认为“两校学生的数学成绩优秀率存在差异”这一结论是否有可能是错误的?
有可能
“两校学生的数学成绩优秀率存在差异 ”这个结论是根据两个频率间存在差异推断出 来的.有可能出现这种情况:在随机抽取的这个样本中,两个频率间确实存在差异,但 两校学生的数学成绩优秀率实际上是没有差别的.对于随机样本而言,因为频率具有随 机性,频率与概率之间存在误差,所以我们的推断可能犯错误,而且在样本容量较小时, 犯错误的可能性会较大.因此,需要找到一种更为合理的推断方法, 同时也希望能对出 现错误推断的概率有一定的控制或估算.
独立性检验方法
假定我们通过简单随机抽样得到了X和Y的抽样数据列联表,如果零假设H0成立,则应
满足 ≈ , 即ad-bc≈0.因此在列联表中|ad-bc|越小,说明两个分类变量之间
关系越弱 ; |ad-bc|越大,说明两个分类变量之间关系越强.
为了使不同样本容量的数据有统一的评判标准 基于上述分析
我们构造一个随机变量
用χ2取值的大小作为判断零假设H0是否成立的依据,当它比较大时推断H0不成 立,否则认为H0成立。这种利用χ2 的取值推断分类变量X和Y是否独立的方法称为χ2 独立性检验,读作“卡方独立性检验 ”,简称独立性检验(test of independence).
3.独立性检验公式及定义
提出零假设(原假设)H0 :分类变量X和Y独立
4.临界值的定义
对于任何小概率值α , 可以找到相应的正实数xα , 使得P(x≥xα)=α成立,我们称xα 为 α 的临界值,这个临界值可作为判断χ2大小的标准,概率值α越小,临界值xα越大.
χ2独立性检验中几个常用的小概率值和相应的临界值.
基于小概率值 α 的检验规则:
当 χ2 ≥x α 时,我们就推断H0不成立,即认为X和Y不独立,该推断犯错误的概率不超过α , 即大约有(1-α) 的可能性认为X和Y有关系;
当 χ20.1 0.05 0.01 0.005
0.001
xα 2.706 3.841 6.635 7.879
10.828
例2 某儿童医院用甲、乙两种疗法治疗小儿消化不良.采用有放回简单随机抽样的方法
对治疗情况进行检查,得到了如下数据:抽到接受甲种疗法的患儿67名,其中未治愈 15名,治愈52名;抽到接受乙种疗法的患儿69名,其中未治愈6名,治愈63名.试根据小概 率值α=0.005的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
解:零假设为H0:疗法与疗效独立,即两种疗法效果没有差异.
将所给数据进行整理,得到两种疗法治疗数据的列联表,
疗法 疗效
合计
未治愈 治愈 甲 15 52
67
乙 6 63
69
合计 21 115
136
没有充分证据推断H0不成立, 因此可以认为 H0成立,即认为 两种疗法效果没有差异.
α 0.1 0.05 0.01 0.005
0.001
xα 2.706 3.841 6.635 7.879
10.828
0.001
52,60
则当m取下面何值时,X与Y的关系最弱
A.8 B.9 √C.14 D.19
解析 由10×26≈18m ,解得m ≈14.4 ,所以当m =14时,X与Y的关系最弱.
y1
y2
x1 10
18
x2 m
26
在列联表中|ad-bc|越小,说明两个分
类变量之间关系越弱 ; |ad-bc|越大, 说明两个分类变量之间关系越强.
3.假设有两个分类变量X与Y,它们的可能取值分别为{x1 ,x2}和{y1,y2},
其2×2列联表为
X Y
合计
Y =0 Y=1 X =0 a b a+b
X=1 c d c+d
合计 a+c b +d n =a+b +c+d
因为|ad-bc|的值越大,两个分类变量有关系的可能性就越大,故选A.
5.在2×2列联表中,两个比值相差越大 , 两个分类变量有关系的可能性就越大 ,那
么这两个比值为 √
6.(1)为了判定两个分类变量X和Y是否有关系,应用独立性检验法算的χ2为5.003 ,又
已知P(χ2 ≥3.841) =0.05 ,P(χ2 ≥6.635) =0.01 ,则下列说法正确的是 ( )
√A.在犯错误的概率不超过5%的前提下,认为“X和Y有关系 ”
B.在犯错误的概率不超过5%的前提下,认为“X和Y没有关系 ”
C.依据小概率值α =0.01的独立性检验,认为“X和Y有关系 ”
D.依据小概率值α =0.01的独立性检验,认为“X和Y没有关系 ”
解: ∵ 3.841 =x0.05<χ2 =5.003<6.635 =x0.01 ,又P(χ2 ≥3.841) =0.05,
: 依据小概率值α =0.05的独立性检验,在犯错误的概率不超过5%的前提 下,即大约95%的可能性认为“X和Y有关系 ”.
xα
α 0.1 0.05 0.01 0.005
0.001
2.706 3.841 6.635 7.879
10.828
(2)有关独立性检验的四个命题,其中不正确的是 ( )
A.两个变量的2×2列联表中,对角线上数据的乘积之差的绝对值越大,
说明两个变量有关系成立的可能性就越大
B.对分类变量X与Y的随机变量χ2来说,χ2越小,认为“X与Y有关系 ”的
犯错误的概率越大
√C.由独立性检验可知:在犯错误的概率不超过5%的前提下,认为秃顶与患心脏病
有关,我们说某人秃顶,那么他有95%的可能患有心脏病
D.依据小概率值α =0.01的独立性检验,认为吸烟与患肺癌有关,是指在犯错误的概 率不超过1%的前提下,即大约有99%的可能性认为吸烟与患肺癌有关
√ √
xα
α 0.1 0.05 0.01 0.005
0.001
2.706 3.841 6.635 7.879
10.828
解析 由题意可知 a>5 ,且15-a>5 ,a∈Z,
8.(多选)针对时下的“抖音热 ”,某校团委对“学生性别和喜欢抖音是否有关 ”作了一次调
查,其中被调查的男女生人数相同,男生喜欢抖音的人数占男生人数的 ,女生喜欢抖音 的人数占女生人数的 ,若在犯错误的概率不超过5%的前提下,认为是否喜欢抖音和性别 有关,则调查人数中男生可能有( )人
A.25 √B.45 √C.60 D.75
解析 设男生的人数为5n(n ∈N*) ,根据题意列出2×2列联表如表所示:
男生 女生
合计
喜欢抖音 4n 3n
7n
不喜欢抖音 n 2n
3n
合计 5n 5n
10n
α 0.1 0.05 0.01 0.005
0.001
xα 2.706 3.841 6.635 7.879
10.828
:n=9,10,11,12
: 5n=45,50,55,60
则x0.05=3.841≤χ2<6.635=x0.01,
得8.066 1≤n<13.933 5,
P67-71
课外资料相应练习
8.3列联表与独立性检验
1.分类变量
在现实生活中,人们经常需要回答一定范围内的两种现象或性质之间 是否存在关联性或互相影响的问题.
例如:就读不同学校是否对学生的成绩有影响,不同班级学生用于
体育锻炼的时间是否存在区别,吸烟是否会增加患肺癌的风险等。
在讨论上述问题时 , 为了表述方便 , 我们经常会使用一种特殊的随机变量 , 以区别 不同的现象或性质 , 这类随机变量称为分类变量.
分类变量:用实数表示不同的现象或性质.
如:班级:1、2、3, 男生、女生:0、1.
本节主要讨论取值于{0,1}的分类变量的关联性
问题1:为了有针对性地提高学生体育锻炼的积极性,某中学需要了解性别因素是否对本
校学生体育锻炼的经常性有影响,为此对学生是否经常锻炼的情况进行了普查.全校生 的普查数据如下:523名女生中有331名经常锻炼,601名男生中有473名经常锻炼.你能利 用这些数据,说明该校女生和男生在体育锻炼的经常性方面是否存在差异吗
解1:比较经常锻炼的学生在女生和男中的比率.
f0 = 经常 生数,f1 = 经常 生数.
≈ 0.633,f1 = ≈ 0.787. f1 0 = 0.787-0.633=0. 154.
男生经常锻炼的比率比女生高出15.4个百分点,所以该校的女生和男生在体育锻 炼的经常性方面有差异,而且男生更经常锻炼.
男生总数
锻炼的男
女生总数
锻炼的女
若性别对体育锻炼的经常性没有影响,可描述为 P (Y = 1 X = 0) = P(Y = 1 X = 1)
若性别对体育锻炼的经常性有影响,可描述为 P (Y = 1 X = 0) ≠ P(Y = 1 X = 1)
性别 锻炼
合计
不经常(Y =0) 经常(Y =1) 女生(X =0) 192 331
523
男生(X =1) 128 473
601
合计 320 804
1124
P(Y = 1X = 1)>P(Y = 1X = 0)
[0,该生不经常锻炼,
Y = {
0,该生为女生,
1,该生为男生,,
解2: 对于Ω中的每一名学生,分别令
∴性别对体育锻炼的经常性有影响
l1 ,该生经常锻炼,
[
X = {
l
X Y
合计
Y =0 Y=1 X =0 a b
a+b
X=1 c d
c+d
合计 a+c b +d
n =a+b +c+d
2.2×2列联表的概念
分类变量X和Y的抽样数据的2×2列联表
2×2列联表给出成对分类变量数据的交叉分类频数
例1.为比较甲、乙两所学校学生的数学水平,采用简单随机抽样的方法抽取88名学生.
通过测验得到了如下数据:甲校43名学生中有10名数学成绩优秀;乙校45名学生中有7名 数学成绩优秀.试分析两校学生中数学成绩优秀率之间是否存在差异.
解:用Ω表示两所学校的全体学生构成的集合.考虑以Ω为样本空间的古典概型.对 于Ω中每一名学生,定义分类变量X和Y如下:
因此,甲校学生中数学成绩不优秀和数学成绩优秀的频率分别为 ≈ 0.7674, ≈ 0.2326.
乙校学生中数学成绩不优秀和数学成绩优秀的频率分别为 ≈ 0.8444, ≈ 0. 1556.
学校 数学成绩
合计
不优秀 Y= 优 = 甲校 (
乙校(X 1) 38 7
合计 71 17
[0, 该生数学成绩不优秀,
Y = {
0, 该生来 自 甲校,
1,该生来 自 乙校,,
l 1 ,该生数学成绩优秀,
[
X = {
l
两个分类变量之间关联关系的定性分析的方法:
(1)频率分析法:通过对样本的每个分类变量的不同类别事件发生的频 率大小进行比较来分析分类变量之间是否有关联关系.
(2)图形分析法:与表格相比,图形更能直观地反映出两个分类变量间是 否互相影响,常用等高堆积条形图展示列联表数据的频率特征.
你认为“两校学生的数学成绩优秀率存在差异”这一结论是否有可能是错误的?
有可能
“两校学生的数学成绩优秀率存在差异 ”这个结论是根据两个频率间存在差异推断出 来的.有可能出现这种情况:在随机抽取的这个样本中,两个频率间确实存在差异,但 两校学生的数学成绩优秀率实际上是没有差别的.对于随机样本而言,因为频率具有随 机性,频率与概率之间存在误差,所以我们的推断可能犯错误,而且在样本容量较小时, 犯错误的可能性会较大.因此,需要找到一种更为合理的推断方法, 同时也希望能对出 现错误推断的概率有一定的控制或估算.
独立性检验方法
假定我们通过简单随机抽样得到了X和Y的抽样数据列联表,如果零假设H0成立,则应
满足 ≈ , 即ad-bc≈0.因此在列联表中|ad-bc|越小,说明两个分类变量之间
关系越弱 ; |ad-bc|越大,说明两个分类变量之间关系越强.
为了使不同样本容量的数据有统一的评判标准 基于上述分析
我们构造一个随机变量
用χ2取值的大小作为判断零假设H0是否成立的依据,当它比较大时推断H0不成 立,否则认为H0成立。这种利用χ2 的取值推断分类变量X和Y是否独立的方法称为χ2 独立性检验,读作“卡方独立性检验 ”,简称独立性检验(test of independence).
3.独立性检验公式及定义
提出零假设(原假设)H0 :分类变量X和Y独立
4.临界值的定义
对于任何小概率值α , 可以找到相应的正实数xα , 使得P(x≥xα)=α成立,我们称xα 为 α 的临界值,这个临界值可作为判断χ2大小的标准,概率值α越小,临界值xα越大.
χ2独立性检验中几个常用的小概率值和相应的临界值.
基于小概率值 α 的检验规则:
当 χ2 ≥x α 时,我们就推断H0不成立,即认为X和Y不独立,该推断犯错误的概率不超过α , 即大约有(1-α) 的可能性认为X和Y有关系;
当 χ2
0.001
xα 2.706 3.841 6.635 7.879
10.828
例2 某儿童医院用甲、乙两种疗法治疗小儿消化不良.采用有放回简单随机抽样的方法
对治疗情况进行检查,得到了如下数据:抽到接受甲种疗法的患儿67名,其中未治愈 15名,治愈52名;抽到接受乙种疗法的患儿69名,其中未治愈6名,治愈63名.试根据小概 率值α=0.005的独立性检验,分析乙种疗法的效果是否比甲种疗法好.
解:零假设为H0:疗法与疗效独立,即两种疗法效果没有差异.
将所给数据进行整理,得到两种疗法治疗数据的列联表,
疗法 疗效
合计
未治愈 治愈 甲 15 52
67
乙 6 63
69
合计 21 115
136
没有充分证据推断H0不成立, 因此可以认为 H0成立,即认为 两种疗法效果没有差异.
α 0.1 0.05 0.01 0.005
0.001
xα 2.706 3.841 6.635 7.879
10.828
0.001
52,60
则当m取下面何值时,X与Y的关系最弱
A.8 B.9 √C.14 D.19
解析 由10×26≈18m ,解得m ≈14.4 ,所以当m =14时,X与Y的关系最弱.
y1
y2
x1 10
18
x2 m
26
在列联表中|ad-bc|越小,说明两个分
类变量之间关系越弱 ; |ad-bc|越大, 说明两个分类变量之间关系越强.
3.假设有两个分类变量X与Y,它们的可能取值分别为{x1 ,x2}和{y1,y2},
其2×2列联表为
X Y
合计
Y =0 Y=1 X =0 a b a+b
X=1 c d c+d
合计 a+c b +d n =a+b +c+d
因为|ad-bc|的值越大,两个分类变量有关系的可能性就越大,故选A.
5.在2×2列联表中,两个比值相差越大 , 两个分类变量有关系的可能性就越大 ,那
么这两个比值为 √
6.(1)为了判定两个分类变量X和Y是否有关系,应用独立性检验法算的χ2为5.003 ,又
已知P(χ2 ≥3.841) =0.05 ,P(χ2 ≥6.635) =0.01 ,则下列说法正确的是 ( )
√A.在犯错误的概率不超过5%的前提下,认为“X和Y有关系 ”
B.在犯错误的概率不超过5%的前提下,认为“X和Y没有关系 ”
C.依据小概率值α =0.01的独立性检验,认为“X和Y有关系 ”
D.依据小概率值α =0.01的独立性检验,认为“X和Y没有关系 ”
解: ∵ 3.841 =x0.05<χ2 =5.003<6.635 =x0.01 ,又P(χ2 ≥3.841) =0.05,
: 依据小概率值α =0.05的独立性检验,在犯错误的概率不超过5%的前提 下,即大约95%的可能性认为“X和Y有关系 ”.
xα
α 0.1 0.05 0.01 0.005
0.001
2.706 3.841 6.635 7.879
10.828
(2)有关独立性检验的四个命题,其中不正确的是 ( )
A.两个变量的2×2列联表中,对角线上数据的乘积之差的绝对值越大,
说明两个变量有关系成立的可能性就越大
B.对分类变量X与Y的随机变量χ2来说,χ2越小,认为“X与Y有关系 ”的
犯错误的概率越大
√C.由独立性检验可知:在犯错误的概率不超过5%的前提下,认为秃顶与患心脏病
有关,我们说某人秃顶,那么他有95%的可能患有心脏病
D.依据小概率值α =0.01的独立性检验,认为吸烟与患肺癌有关,是指在犯错误的概 率不超过1%的前提下,即大约有99%的可能性认为吸烟与患肺癌有关
√ √
xα
α 0.1 0.05 0.01 0.005
0.001
2.706 3.841 6.635 7.879
10.828
解析 由题意可知 a>5 ,且15-a>5 ,a∈Z,
8.(多选)针对时下的“抖音热 ”,某校团委对“学生性别和喜欢抖音是否有关 ”作了一次调
查,其中被调查的男女生人数相同,男生喜欢抖音的人数占男生人数的 ,女生喜欢抖音 的人数占女生人数的 ,若在犯错误的概率不超过5%的前提下,认为是否喜欢抖音和性别 有关,则调查人数中男生可能有( )人
A.25 √B.45 √C.60 D.75
解析 设男生的人数为5n(n ∈N*) ,根据题意列出2×2列联表如表所示:
男生 女生
合计
喜欢抖音 4n 3n
7n
不喜欢抖音 n 2n
3n
合计 5n 5n
10n
α 0.1 0.05 0.01 0.005
0.001
xα 2.706 3.841 6.635 7.879
10.828
:n=9,10,11,12
: 5n=45,50,55,60
则x0.05=3.841≤χ2<6.635=x0.01,
得8.066 1≤n<13.933 5,
P67-71
课外资料相应练习
