人教版五年级数学上册平行四边形的面积课件(共15张PPT)
文档属性
| 名称 | 人教版五年级数学上册平行四边形的面积课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-05 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
平行四边形的面积
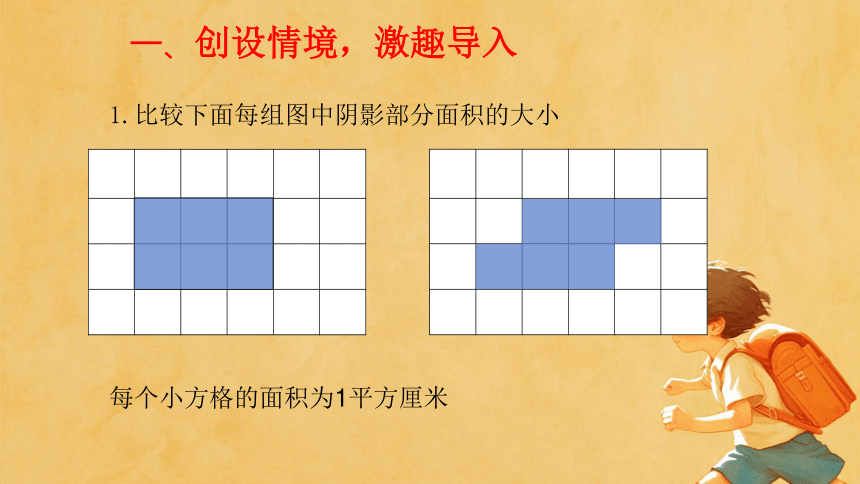
一、创设情境,激趣导入
1.比较下面每组图中阴影部分面积的大小
每个小方格的面积为1平方厘米
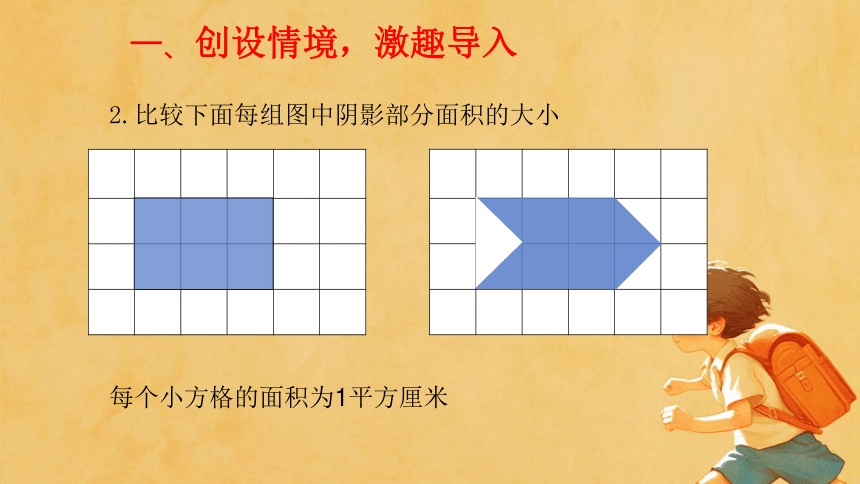
2.比较下面每组图中阴影部分面积的大小
每个小方格的面积为1平方厘米
一、创设情境,激趣导入
二、主动探索,推导公式
平行四边形的面积如何算呢?
可能是...
可能是...
二、主动探索,推导公式
我猜平行四边形的面积是?
二、主动探索,推导公式
不数方格,能不能计算平行四边形的面积?
想一想:该怎么做?
转化
二、主动探索,推导公式
高
底
宽
长
高
宽
底
长
平行四边形
转化成
长方形
二、主动探索,推导公式
如果用 S 表示平行四边形的面积,用 a 表示平行四边形的底,用 h 表示平行四边形的高,平行四边形的面积计算公式可以写成:___________。
S = ah
二、主动探索,推导公式
平行四边形花坛的底是 6 m,高是 4 m,它的面积是多少?
S = ah
= 6×4
= 24(m2)
答:平行四边形花坛的面积是 24 m2。
三、巩固运用、解决问题
1.计算下面平行四边形的面积。
S = ah
= 4×3
= 12(cm2)
S = ah
= 5.2×3.6
=18.72(cm2)
S = ah
= 2×2.4
= 4.8(cm2)
四、变式练习,内化提高
S = ah
= 4×3
= 12(cm2)
S = ah
= 4×3
= 12(cm2)
四、变式练习,内化提高
2.一块平行四边形木板,底是4cm,高是3cm。它的面积是多少?
你能算出它的面积吗?
你能在方格纸上画出这样的平行四边形吗?
下面每个小格代表1
四、变式练习,内化提高
我发现了:
等底等高的平行四边形的面积相等。
这节课你有什么收获
五、全课总结,畅谈收获
平行四边形的面积
一、创设情境,激趣导入
1.比较下面每组图中阴影部分面积的大小
每个小方格的面积为1平方厘米
2.比较下面每组图中阴影部分面积的大小
每个小方格的面积为1平方厘米
一、创设情境,激趣导入
二、主动探索,推导公式
平行四边形的面积如何算呢?
可能是...
可能是...
二、主动探索,推导公式
我猜平行四边形的面积是?
二、主动探索,推导公式
不数方格,能不能计算平行四边形的面积?
想一想:该怎么做?
转化
二、主动探索,推导公式
高
底
宽
长
高
宽
底
长
平行四边形
转化成
长方形
二、主动探索,推导公式
如果用 S 表示平行四边形的面积,用 a 表示平行四边形的底,用 h 表示平行四边形的高,平行四边形的面积计算公式可以写成:___________。
S = ah
二、主动探索,推导公式
平行四边形花坛的底是 6 m,高是 4 m,它的面积是多少?
S = ah
= 6×4
= 24(m2)
答:平行四边形花坛的面积是 24 m2。
三、巩固运用、解决问题
1.计算下面平行四边形的面积。
S = ah
= 4×3
= 12(cm2)
S = ah
= 5.2×3.6
=18.72(cm2)
S = ah
= 2×2.4
= 4.8(cm2)
四、变式练习,内化提高
S = ah
= 4×3
= 12(cm2)
S = ah
= 4×3
= 12(cm2)
四、变式练习,内化提高
2.一块平行四边形木板,底是4cm,高是3cm。它的面积是多少?
你能算出它的面积吗?
你能在方格纸上画出这样的平行四边形吗?
下面每个小格代表1
四、变式练习,内化提高
我发现了:
等底等高的平行四边形的面积相等。
这节课你有什么收获
五、全课总结,畅谈收获
