重庆市鲁能巴蜀中学2024-2025学年 八年级上学期开学数学测试(线上)1(图片版,无答案)
文档属性
| 名称 | 重庆市鲁能巴蜀中学2024-2025学年 八年级上学期开学数学测试(线上)1(图片版,无答案) | 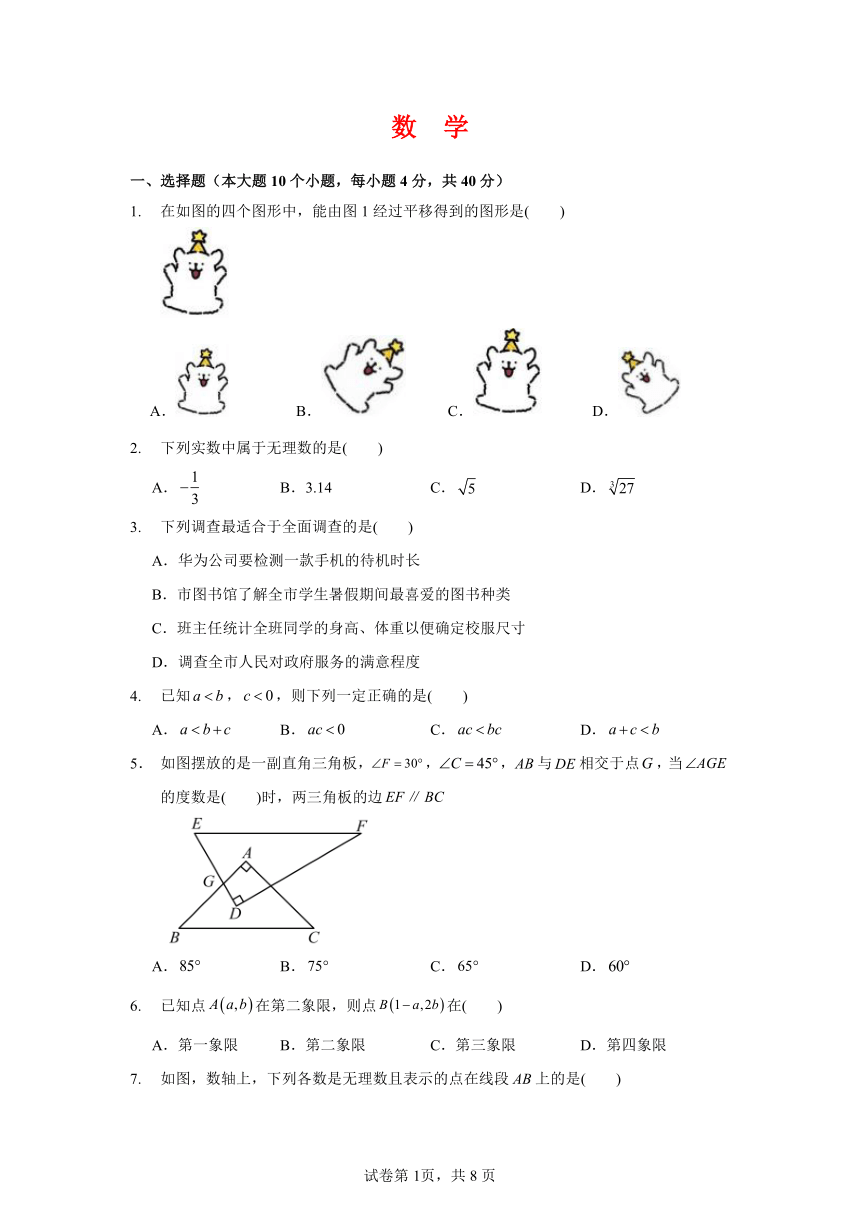 | |
| 格式 | |||
| 文件大小 | 444.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-05 20:52:11 | ||
图片预览



文档简介
数 学
一、选择题(本大题 10 个小题,每小题 4 分,共 40 分)
1. 在如图的四个图形中,能由图 1经过平移得到的图形是( )
A. B. C. D.
2. 下列实数中属于无理数的是( )
1
A. B.3.14 C. 5 D. 3 27
3
3. 下列调查最适合于全面调查的是( )
A.华为公司要检测一款手机的待机时长
B.市图书馆了解全市学生暑假期间最喜爱的图书种类
C.班主任统计全班同学的身高、体重以便确定校服尺寸
D.调查全市人民对政府服务的满意程度
4. 已知 a b, c 0,则下列一定正确的是( )
A.a b c B. ac 0 C. ac bc D. a c b
5. 如图摆放的是一副直角三角板, F 30 , C 45 ,AB与DE相交于点G,当 AGE
的度数是( )时,两三角板的边 EF∥BC
A.85 B.75 C.65 D.60
6. 已知点 A a,b 在第二象限,则点 B 1 a,2b 在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7. 如图,数轴上,下列各数是无理数且表示的点在线段 AB上的是( )
试卷第 1页,共 8页
{#{QQABZYA0U4ogiA4gIANIBSACARBg5CL E0wFE8YCCAAoIQskIBGCgALcAgQsgAOQhCBPAKIIAAQAKAQwYQFFABIAA=}=#}}#}
A.0 B. 2 1 C. 3 9 D.
8. 如图,在Rt ABC中, C 90 , AC 8, BC 6, AB 10, CAB和 ABC的平
分线交于点O,OM BC于点M ,则OM 的长为( )
A.1 B.2 C.3 D.4
x y 69. 若数 a既使得关于 x、y的二元一次方程组 有正整数解,又使得关于 x的
3x 2y a 3
3x 5
x a
不等式组 2 的解集为 x 15,那么所有满足条件的 a的值之和为 ( )
3 2x 3
9
A. 15 B. 30 C. 10 D.0
10. 将 1,2, 3 n这 n个数据顺时针排成一圈,从 1开始,顺时针方向采取保留一个划去
一个的规则,直至只留下一个数,将这个数记为 an.当 n取不同值时,可得到对应情况
下的 an,并将所有 an形成一组新数据.下列说法中,正确的个数为 ( )
①无论 n为多少, an一定为奇数;
② a2 a4 a8 a16 1;
S 2
③记 an的前 n项和为 S 16n ,则 1;S17
④当 n从 1取到 18时,将形成的新数据 an依次顺时针排成一圈,从 a1开始,再进行同
一种操作,最后留下来的数为 3.
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题 8 个小题,每小题 4 分,共 32 分)
11. 64 的立方根是_______.
试卷第 2页,共 8页
{#{QQABZYAU04ogiA4gIANIBSACARB5gLCE0wFE8YCCAAoIQskIBGCgALcAgQsgAOQhCBPAKIIAAQAKAQwYQFFABIAA=}=#}}#}
12. 一个等腰三角形的两边长分别是 2cm、5cm,则它的周长为 cm.
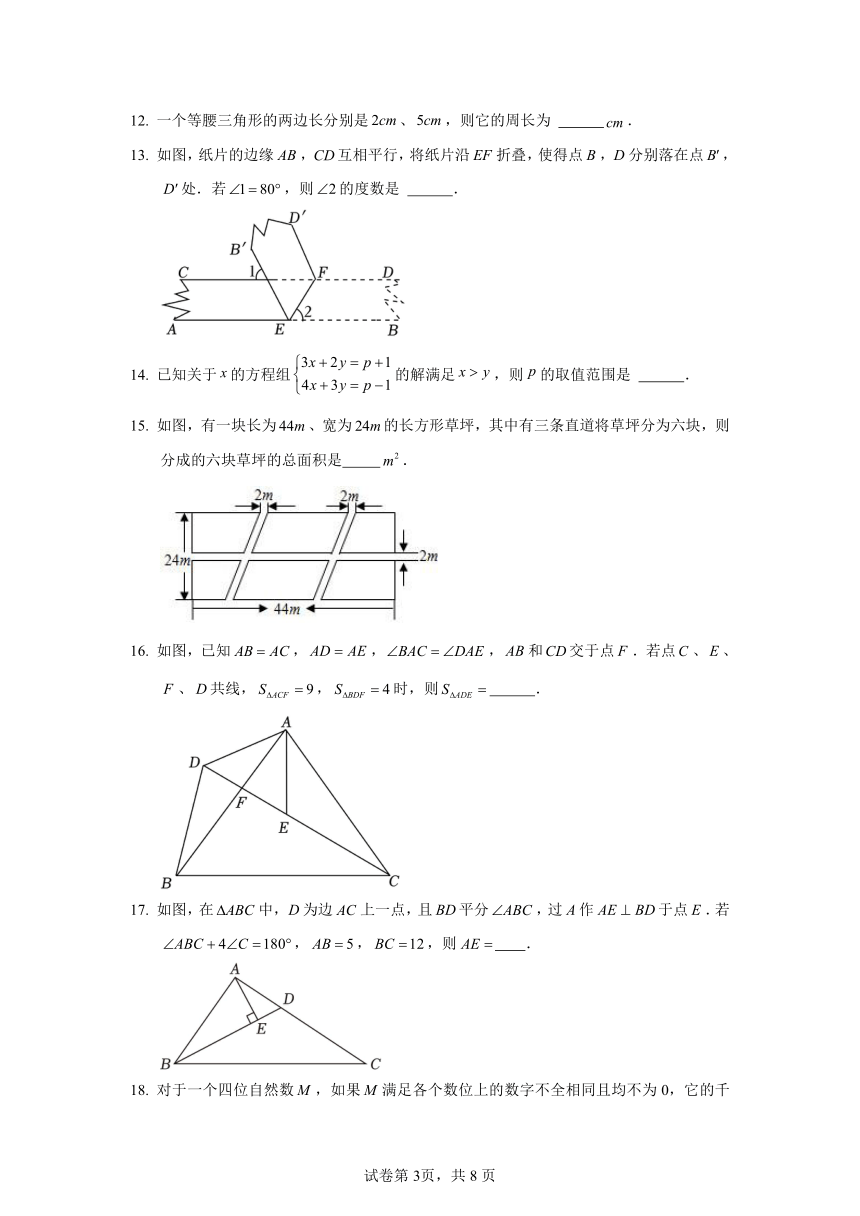
13. 如图,纸片的边缘 AB,CD互相平行,将纸片沿 EF 折叠,使得点 B,D分别落在点 B ,
D 处.若 1 80 ,则 2的度数是 .
3x 2y p 1
14. 已知关于 x的方程组 x y p
4x 3y p 1
的解满足 ,则 的取值范围是 .
15. 如图,有一块长为 44m、宽为 24m的长方形草坪,其中有三条直道将草坪分为六块,则
分成的六块草坪的总面积是 m2 .
16. 如图,已知 AB AC,AD AE, BAC DAE ,AB和CD交于点 F .若点C、E、
F 、D共线, S ACF 9, S BDF 4时,则 S ADE .
17. 如图,在 ABC中,D为边 AC上一点,且 BD平分 ABC,过 A作 AE BD于点 E.若
ABC 4 C 180 , AB 5, BC 12,则 AE .
18. 对于一个四位自然数M ,如果M 满足各个数位上的数字不全相同且均不为 0,它的千
试卷第 3页,共 8页
{#{QQABZYAU04ogiA4gIANISBAACRBg5CL E0wFE8YCCAAoIQskIBGCgALcAgQsgAOQhCBPAKIIAAQAKAQwYQFFABIAA=}=#}}#}
位数字减去百位数字之差等于十位数字减去个位数字之差,那么称这个数M 为“均衡
数”.对于一个“均衡数” M ,将它的前两位数减去后两位数所得记为 s,将它的千位
s t
和十位构成的两位数减去百位和个位构成的两位数所得差记为 t,定: F (M ) ,
11
例如:M 9764,因为 9 7 6 4,故:9764是一个“均衡数”,所以:s 97 64 33,
t 96 74 22 33 22,则: F (9764) 5 .若自然数 P , Q都是“均衡数”,其中
11
P 1000x 10y 515 ,Q 100m n 2041(2 x 9 , 2 y 9,1 m 9, 0 n 8, x,
y F (P),m,n都是整数),规定:k ,当 F (P) 2F (Q) 8时,k的最大值是_________.
F (Q)
三、解答题:(本大题 8 个小题,共 78 分)解答时每小题必须给出必要的演算过程或推理
步骤,请将解答过程书写在答题卡中对应的位置上.
19. 计算:
(1) a 2 a 3; (2) 2a b a 2b 2a b 2.
20. 因式分解:
(1)x3 2x2 y xy2 (2)x2(a 1) y2(1 a)
21. 人教版八年级上册教材第 80页利用将两个含有 30 角的全等三角尺摆在一起的方法,借
助图形发现了结论:“在直角三角形中,如果有一个锐角等于 30 ,那么它所对的直角
边等于斜边的一半.”我们还能用其他的方法证明这个结论吗?
下面是小明的探究过程,请根据他的思路完成以下作图和填空:
1
如图,在 ABC中, ACB 90 , ABC 30 ,求证: AC AB.
2
(1)尺规作图:作 CAB的角平分线交 BC于点 D,在 AB上取一点 E,使得 AE AC ,
连接DE(保留作图痕迹,不写作法);
(2)证明: ACB 90 , ABC 30 ,
CAB 60 ,
AD平分 CAB,
CAD ① 30 ,
试卷第 4页,共 8页
{#{QQABZYA0U4ogiA4gIANISBAACRBg5LCE0wFE8YCCAAoIQskIBGCgALcAgQsgAOQhCBPAKIIAAQAKAQwYQFFABIAA=}=#}}#}
在 ADC与 ADE中,
AC AE
CAD EAD,
AD AD
ACD AED(SAS ),
ACB ② 90 ,
DE AB,
又: ABC EAD 30 ,
DA ③ ,
点 E是 AB的中点.
1
④ AB,
2
AC AE,
AC 1 AB.
2
22. 推行“减负增效”政策后,为了解九年级学生每天自主学习的时长情况,学校随机抽取
部分九年级学生进行调查,按四个组别;A组 (0.5小时),B组 (1小时),C 组 (1.5小时),
D组 (2小时)进行整理,绘制如下两幅不完整的统计图,根据图中提供的信息,解决
下列问题:
(1)本次调查的学生人数是 人; A组 (0.5小时)在扇形统计图中的圆心角 的
大小是 ;
(2)将条形统计图补充完整;
试卷第 5页,共 8页
{#{QQABZYAU04ogiA4gIANISBAACRB5gCL E0wFE8YCCAAoIQskIBGCgALcAgQsgAOQhCBPAKIIAAQAKAQwYQFFABIAA=}=#}}#}
(3)若该校九年级有 600 名学生,请估计其中每天自主学习时间不少于 1.5小时的学
生人数.
23. 如图,点 B、C、D在同一条直线上, AB BD, DE BD, AC CE, AB CD.
(1)求证: ABC CDE.
(2)若 ACB 37 ,求 AED的度数.
24. 某水果店销售 A、B两种规格的水果礼盒,A进货价为每盒 60元,B进货价为每盒 45
元.表格中是该水果店近两周这两种水果礼盒的销售情况.(进价保持不变,不考虑水
果变质等损耗)
销售时段 周销售数量 周销售总利润
第一周 40盒 A水果礼盒 85盒 B水果礼盒 2075元
第二周 60盒 A水果礼盒 100盒 B水果礼盒 2700元
(1)若这两周售价保持不变,求这两种规格水果礼盒的售价分别为每盒多少元?
(2)第三周,该店决定恰好 9000元购进 A、B两种水果礼盒,A水果礼盒按售价打九
折进行促销,而 B水果礼盒则按利润率为 40%定价,使得第三周总利润至少为 3000
元,且 A、B两种水果礼盒全部售完,求第三周最多进货 A水果礼盒多少盒?
试卷第 6页,共 8页
{#{QQABZYAU04ogiA4gIANIBSACARB5gLCE0wFE8YCCAAoIQskIBGCgALcAgQsgAOQhCBPAKIIAAQAKAQwYQFFABIAA=}=#}}#}
25. 在平面直角坐标系 xOy中,对于任意三点 A, B,C的“矩面积”,给出如下定义:“水平底” d是
任意两点横坐标差的最大值;“铅垂高” h是任意两点纵坐标差的最大值,则“矩面积” S dh.例
如:A,B,C三点的坐标分别为 (1,2),( 3,1),(2, 2),则“水平底”d 5,“铅垂高”h 4,“矩
面积” S dh 20.根据所给定义解决下面的问题:
(1)若点D, E, F 的坐标分别为 ( 1,2), (2, 1), (0,6),求这三点的“矩面积” S;
(2)若点D(2,3), E(2, 1), F (t, 2)(t 2),含有 t的式子表示这三点的“矩面积” S(结果需化
简);
(3)已知点 D( 1,2), E(2, 2),在 x轴上是否存在点 F ,使这三点的“矩面积” S为 20?若存在,
求出点 F 的坐标;若不存在,请说明理由.
试卷第 7页,共 8页
{#{QQABZYA0U4ogiA4gIANISBAACRBg5LCE0wFE8YCCAAoIQskIBGCgALcAgQsgAOQhCBPAKIIAAQAKAQwYQFFABIAA=}=#}}#}
26. 如 图 , CAB 与 CDE 为 等 腰 直 角 三 角 形 , ACB DCE 90 , CA CB , CD CE ,
CAB CBA 45 , CDE CED 45 ,连接 AD、 BE .
(1)如图 1,若 CAD 28 , DCB 10 ,则 DEB的度数为 度;
(2)如图 2,若 A、D、E三点共线,AE与 BC交于点 F ,且CF BF ,AD 3,求 CEF 的面积;
(3)如图 3, BE 与 AC的延长线交于点G ,若CD AD,延长CD与 AB交于点 N,在 BC上有一
点M 且 BM CG,连接 NM ,请猜想CN 、 NM 、 BG 之间的数量关系并证明你的猜想.
试卷第 8页,共 8页
{#{QQABZYAU04ogiA4gIANIBSACARB5gLCE0wFE8YCCAAoIQskIBGCgALcAgQsgAOQhCBPAKIIAAQAKAQwYQFFABIAA=}=#}}#}
一、选择题(本大题 10 个小题,每小题 4 分,共 40 分)
1. 在如图的四个图形中,能由图 1经过平移得到的图形是( )
A. B. C. D.
2. 下列实数中属于无理数的是( )
1
A. B.3.14 C. 5 D. 3 27
3
3. 下列调查最适合于全面调查的是( )
A.华为公司要检测一款手机的待机时长
B.市图书馆了解全市学生暑假期间最喜爱的图书种类
C.班主任统计全班同学的身高、体重以便确定校服尺寸
D.调查全市人民对政府服务的满意程度
4. 已知 a b, c 0,则下列一定正确的是( )
A.a b c B. ac 0 C. ac bc D. a c b
5. 如图摆放的是一副直角三角板, F 30 , C 45 ,AB与DE相交于点G,当 AGE
的度数是( )时,两三角板的边 EF∥BC
A.85 B.75 C.65 D.60
6. 已知点 A a,b 在第二象限,则点 B 1 a,2b 在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7. 如图,数轴上,下列各数是无理数且表示的点在线段 AB上的是( )
试卷第 1页,共 8页
{#{QQABZYA0U4ogiA4gIANIBSACARBg5CL E0wFE8YCCAAoIQskIBGCgALcAgQsgAOQhCBPAKIIAAQAKAQwYQFFABIAA=}=#}}#}
A.0 B. 2 1 C. 3 9 D.
8. 如图,在Rt ABC中, C 90 , AC 8, BC 6, AB 10, CAB和 ABC的平
分线交于点O,OM BC于点M ,则OM 的长为( )
A.1 B.2 C.3 D.4
x y 69. 若数 a既使得关于 x、y的二元一次方程组 有正整数解,又使得关于 x的
3x 2y a 3
3x 5
x a
不等式组 2 的解集为 x 15,那么所有满足条件的 a的值之和为 ( )
3 2x 3
9
A. 15 B. 30 C. 10 D.0
10. 将 1,2, 3 n这 n个数据顺时针排成一圈,从 1开始,顺时针方向采取保留一个划去
一个的规则,直至只留下一个数,将这个数记为 an.当 n取不同值时,可得到对应情况
下的 an,并将所有 an形成一组新数据.下列说法中,正确的个数为 ( )
①无论 n为多少, an一定为奇数;
② a2 a4 a8 a16 1;
S 2
③记 an的前 n项和为 S 16n ,则 1;S17
④当 n从 1取到 18时,将形成的新数据 an依次顺时针排成一圈,从 a1开始,再进行同
一种操作,最后留下来的数为 3.
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题 8 个小题,每小题 4 分,共 32 分)
11. 64 的立方根是_______.
试卷第 2页,共 8页
{#{QQABZYAU04ogiA4gIANIBSACARB5gLCE0wFE8YCCAAoIQskIBGCgALcAgQsgAOQhCBPAKIIAAQAKAQwYQFFABIAA=}=#}}#}
12. 一个等腰三角形的两边长分别是 2cm、5cm,则它的周长为 cm.
13. 如图,纸片的边缘 AB,CD互相平行,将纸片沿 EF 折叠,使得点 B,D分别落在点 B ,
D 处.若 1 80 ,则 2的度数是 .
3x 2y p 1
14. 已知关于 x的方程组 x y p
4x 3y p 1
的解满足 ,则 的取值范围是 .
15. 如图,有一块长为 44m、宽为 24m的长方形草坪,其中有三条直道将草坪分为六块,则
分成的六块草坪的总面积是 m2 .
16. 如图,已知 AB AC,AD AE, BAC DAE ,AB和CD交于点 F .若点C、E、
F 、D共线, S ACF 9, S BDF 4时,则 S ADE .
17. 如图,在 ABC中,D为边 AC上一点,且 BD平分 ABC,过 A作 AE BD于点 E.若
ABC 4 C 180 , AB 5, BC 12,则 AE .
18. 对于一个四位自然数M ,如果M 满足各个数位上的数字不全相同且均不为 0,它的千
试卷第 3页,共 8页
{#{QQABZYAU04ogiA4gIANISBAACRBg5CL E0wFE8YCCAAoIQskIBGCgALcAgQsgAOQhCBPAKIIAAQAKAQwYQFFABIAA=}=#}}#}
位数字减去百位数字之差等于十位数字减去个位数字之差,那么称这个数M 为“均衡
数”.对于一个“均衡数” M ,将它的前两位数减去后两位数所得记为 s,将它的千位
s t
和十位构成的两位数减去百位和个位构成的两位数所得差记为 t,定: F (M ) ,
11
例如:M 9764,因为 9 7 6 4,故:9764是一个“均衡数”,所以:s 97 64 33,
t 96 74 22 33 22,则: F (9764) 5 .若自然数 P , Q都是“均衡数”,其中
11
P 1000x 10y 515 ,Q 100m n 2041(2 x 9 , 2 y 9,1 m 9, 0 n 8, x,
y F (P),m,n都是整数),规定:k ,当 F (P) 2F (Q) 8时,k的最大值是_________.
F (Q)
三、解答题:(本大题 8 个小题,共 78 分)解答时每小题必须给出必要的演算过程或推理
步骤,请将解答过程书写在答题卡中对应的位置上.
19. 计算:
(1) a 2 a 3; (2) 2a b a 2b 2a b 2.
20. 因式分解:
(1)x3 2x2 y xy2 (2)x2(a 1) y2(1 a)
21. 人教版八年级上册教材第 80页利用将两个含有 30 角的全等三角尺摆在一起的方法,借
助图形发现了结论:“在直角三角形中,如果有一个锐角等于 30 ,那么它所对的直角
边等于斜边的一半.”我们还能用其他的方法证明这个结论吗?
下面是小明的探究过程,请根据他的思路完成以下作图和填空:
1
如图,在 ABC中, ACB 90 , ABC 30 ,求证: AC AB.
2
(1)尺规作图:作 CAB的角平分线交 BC于点 D,在 AB上取一点 E,使得 AE AC ,
连接DE(保留作图痕迹,不写作法);
(2)证明: ACB 90 , ABC 30 ,
CAB 60 ,
AD平分 CAB,
CAD ① 30 ,
试卷第 4页,共 8页
{#{QQABZYA0U4ogiA4gIANISBAACRBg5LCE0wFE8YCCAAoIQskIBGCgALcAgQsgAOQhCBPAKIIAAQAKAQwYQFFABIAA=}=#}}#}
在 ADC与 ADE中,
AC AE
CAD EAD,
AD AD
ACD AED(SAS ),
ACB ② 90 ,
DE AB,
又: ABC EAD 30 ,
DA ③ ,
点 E是 AB的中点.
1
④ AB,
2
AC AE,
AC 1 AB.
2
22. 推行“减负增效”政策后,为了解九年级学生每天自主学习的时长情况,学校随机抽取
部分九年级学生进行调查,按四个组别;A组 (0.5小时),B组 (1小时),C 组 (1.5小时),
D组 (2小时)进行整理,绘制如下两幅不完整的统计图,根据图中提供的信息,解决
下列问题:
(1)本次调查的学生人数是 人; A组 (0.5小时)在扇形统计图中的圆心角 的
大小是 ;
(2)将条形统计图补充完整;
试卷第 5页,共 8页
{#{QQABZYAU04ogiA4gIANISBAACRB5gCL E0wFE8YCCAAoIQskIBGCgALcAgQsgAOQhCBPAKIIAAQAKAQwYQFFABIAA=}=#}}#}
(3)若该校九年级有 600 名学生,请估计其中每天自主学习时间不少于 1.5小时的学
生人数.
23. 如图,点 B、C、D在同一条直线上, AB BD, DE BD, AC CE, AB CD.
(1)求证: ABC CDE.
(2)若 ACB 37 ,求 AED的度数.
24. 某水果店销售 A、B两种规格的水果礼盒,A进货价为每盒 60元,B进货价为每盒 45
元.表格中是该水果店近两周这两种水果礼盒的销售情况.(进价保持不变,不考虑水
果变质等损耗)
销售时段 周销售数量 周销售总利润
第一周 40盒 A水果礼盒 85盒 B水果礼盒 2075元
第二周 60盒 A水果礼盒 100盒 B水果礼盒 2700元
(1)若这两周售价保持不变,求这两种规格水果礼盒的售价分别为每盒多少元?
(2)第三周,该店决定恰好 9000元购进 A、B两种水果礼盒,A水果礼盒按售价打九
折进行促销,而 B水果礼盒则按利润率为 40%定价,使得第三周总利润至少为 3000
元,且 A、B两种水果礼盒全部售完,求第三周最多进货 A水果礼盒多少盒?
试卷第 6页,共 8页
{#{QQABZYAU04ogiA4gIANIBSACARB5gLCE0wFE8YCCAAoIQskIBGCgALcAgQsgAOQhCBPAKIIAAQAKAQwYQFFABIAA=}=#}}#}
25. 在平面直角坐标系 xOy中,对于任意三点 A, B,C的“矩面积”,给出如下定义:“水平底” d是
任意两点横坐标差的最大值;“铅垂高” h是任意两点纵坐标差的最大值,则“矩面积” S dh.例
如:A,B,C三点的坐标分别为 (1,2),( 3,1),(2, 2),则“水平底”d 5,“铅垂高”h 4,“矩
面积” S dh 20.根据所给定义解决下面的问题:
(1)若点D, E, F 的坐标分别为 ( 1,2), (2, 1), (0,6),求这三点的“矩面积” S;
(2)若点D(2,3), E(2, 1), F (t, 2)(t 2),含有 t的式子表示这三点的“矩面积” S(结果需化
简);
(3)已知点 D( 1,2), E(2, 2),在 x轴上是否存在点 F ,使这三点的“矩面积” S为 20?若存在,
求出点 F 的坐标;若不存在,请说明理由.
试卷第 7页,共 8页
{#{QQABZYA0U4ogiA4gIANISBAACRBg5LCE0wFE8YCCAAoIQskIBGCgALcAgQsgAOQhCBPAKIIAAQAKAQwYQFFABIAA=}=#}}#}
26. 如 图 , CAB 与 CDE 为 等 腰 直 角 三 角 形 , ACB DCE 90 , CA CB , CD CE ,
CAB CBA 45 , CDE CED 45 ,连接 AD、 BE .
(1)如图 1,若 CAD 28 , DCB 10 ,则 DEB的度数为 度;
(2)如图 2,若 A、D、E三点共线,AE与 BC交于点 F ,且CF BF ,AD 3,求 CEF 的面积;
(3)如图 3, BE 与 AC的延长线交于点G ,若CD AD,延长CD与 AB交于点 N,在 BC上有一
点M 且 BM CG,连接 NM ,请猜想CN 、 NM 、 BG 之间的数量关系并证明你的猜想.
试卷第 8页,共 8页
{#{QQABZYAU04ogiA4gIANIBSACARB5gLCE0wFE8YCCAAoIQskIBGCgALcAgQsgAOQhCBPAKIIAAQAKAQwYQFFABIAA=}=#}}#}
同课章节目录
