22.1.4 第2课时 用待定系数法求二次函数的解析式 同步练(无答案) 2024-2025学年数学人教版九年级上册
文档属性
| 名称 | 22.1.4 第2课时 用待定系数法求二次函数的解析式 同步练(无答案) 2024-2025学年数学人教版九年级上册 |

|
|
| 格式 | zip | ||
| 文件大小 | 124.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-05 00:00:00 | ||
图片预览

文档简介
第2课时 用待定系数法求二次函数的解析式
知识点1 设一般式y=ax2+bx+c求二次函数解析式
1[教材再开发·P39探究变式]已知抛物线经过A(-1,0),B(0,-3),C(3,0)三点,则抛物线的解析式是 .
2若抛物线经过点(3,0)和(2,-3),且以直线x=1为对称轴,则该抛物线的解析式为( )
A.y=-x2-2x-3
B.y=x2-2x+3
C.y=x2-2x-3
D.y=-x2+2x-3
3[教材再开发·P40练习T2变式]二次函数y=ax2+bx+c(a≠0)的图象过A(-1,0),B(2,0),C(0,-2)三点,则此二次函数的解析式是 .
4若二次函数y=x2+bx+c的图象经过A(0,2),B(1,0)两点.
(1)求b,c的值.
(2)将该二次函数的解析式化为y=a(x-h)2+k的形式,h=________ ,k=________ .
知识点2 设顶点式y=a(x-h)2+k求二次函数解析式
5若抛物线的顶点为(2,3)且抛物线经过点(3,1),那么抛物线解析式是( )
A.y=4(x-2)2-3 B.y=-2(x-2)2+3
C.y=-2(x-2)2-3 D.y=-(x-2)2+3
6已知二次函数y=ax2+bx+c的图象如图所示,则这个二次函数的解析式是 .
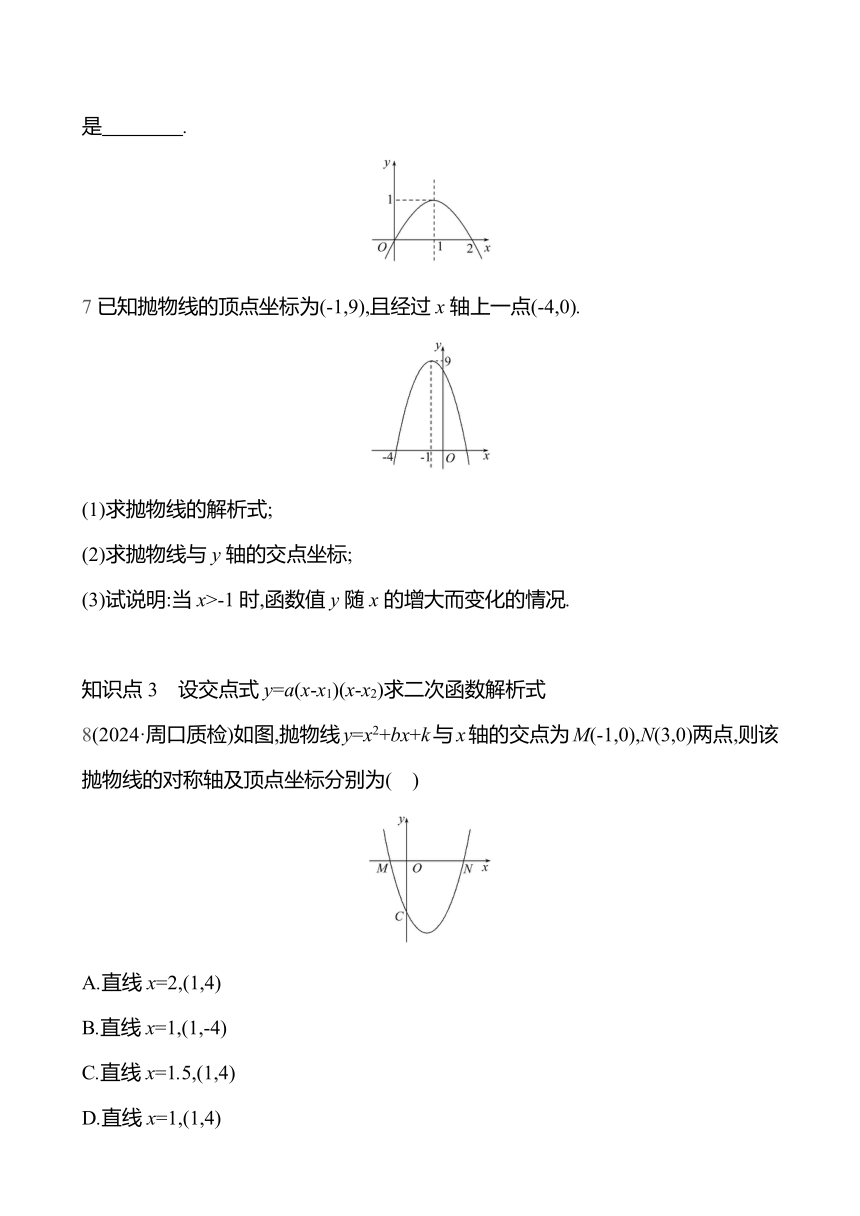
7已知抛物线的顶点坐标为(-1,9),且经过x轴上一点(-4,0).
(1)求抛物线的解析式;
(2)求抛物线与y轴的交点坐标;
(3)试说明:当x>-1时,函数值y随x的增大而变化的情况.
知识点3 设交点式y=a(x-x1)(x-x2)求二次函数解析式
8(2024·周口质检)如图,抛物线y=x2+bx+k与x轴的交点为M(-1,0),N(3,0)两点,则该抛物线的对称轴及顶点坐标分别为( )
A.直线x=2,(1,4)
B.直线x=1,(1,-4)
C.直线x=1.5,(1,4)
D.直线x=1,(1,4)
9写出一个开口向下,且过(-1,0)和(5,0)的二次函数的解析式: .
10(2024·苏州期中)将抛物线y=ax2+bx+c(a≠0)的图象向右平移3个单位长度,下列说法正确的是( )
A.对称轴没有改变
B.顶点坐标没有改变
C.开口方向改变
D.函数最值没有改变
11如图,在平面直角坐标系xOy中,抛物线y=ax2+2ax+c与x轴交于A,B两点(点A在点B的左侧),且AB=4,则点A的坐标为( )
A.(1,0) B.(-1,0)
C.(3,0) D.(-3,0)
12(2024·滁州期中)如图,抛物线y=-x2+bx+c与x轴,y轴分别交于A,B两点.若OA=OB,则下列结论成立的是( )
A.4b-c=1 B.b+4c=1
C.4b-c=4 D.4b+c=4
13已知一个二次函数的图象与x轴的交点为(-2,0),(4,0),且顶点在函数y=2x的图象上,则这个函数的解析式是 .
14在平面直角坐标系中,函数y=x2+x-2的图象关于x轴作轴对称变换,变换后所得的抛物线的解析式为 .
15新趋势·模型观念、几何直观
某次数学活动时,数学兴趣小组成员小融拟研究函数y=-(x-2)2+|x-2|+3的图象和性质.
(1)如表是该函数y与自变量x的几组对应值:
x … -2 -1 0 1 2 3 4 5 6 …
y … -1 1.5 m 3.5 3 n 3 1.5 -1 …
其中,m的值为________,n的值为________;
(2)如图,在平面直角坐标系xOy中,描出上表中各组对应值为坐标的点,再根据描出的点,画出该函数图象;
(3)根据函数图象,写出该函数的一条性质:________________________________.
知识点1 设一般式y=ax2+bx+c求二次函数解析式
1[教材再开发·P39探究变式]已知抛物线经过A(-1,0),B(0,-3),C(3,0)三点,则抛物线的解析式是 .
2若抛物线经过点(3,0)和(2,-3),且以直线x=1为对称轴,则该抛物线的解析式为( )
A.y=-x2-2x-3
B.y=x2-2x+3
C.y=x2-2x-3
D.y=-x2+2x-3
3[教材再开发·P40练习T2变式]二次函数y=ax2+bx+c(a≠0)的图象过A(-1,0),B(2,0),C(0,-2)三点,则此二次函数的解析式是 .
4若二次函数y=x2+bx+c的图象经过A(0,2),B(1,0)两点.
(1)求b,c的值.
(2)将该二次函数的解析式化为y=a(x-h)2+k的形式,h=________ ,k=________ .
知识点2 设顶点式y=a(x-h)2+k求二次函数解析式
5若抛物线的顶点为(2,3)且抛物线经过点(3,1),那么抛物线解析式是( )
A.y=4(x-2)2-3 B.y=-2(x-2)2+3
C.y=-2(x-2)2-3 D.y=-(x-2)2+3
6已知二次函数y=ax2+bx+c的图象如图所示,则这个二次函数的解析式是 .
7已知抛物线的顶点坐标为(-1,9),且经过x轴上一点(-4,0).
(1)求抛物线的解析式;
(2)求抛物线与y轴的交点坐标;
(3)试说明:当x>-1时,函数值y随x的增大而变化的情况.
知识点3 设交点式y=a(x-x1)(x-x2)求二次函数解析式
8(2024·周口质检)如图,抛物线y=x2+bx+k与x轴的交点为M(-1,0),N(3,0)两点,则该抛物线的对称轴及顶点坐标分别为( )
A.直线x=2,(1,4)
B.直线x=1,(1,-4)
C.直线x=1.5,(1,4)
D.直线x=1,(1,4)
9写出一个开口向下,且过(-1,0)和(5,0)的二次函数的解析式: .
10(2024·苏州期中)将抛物线y=ax2+bx+c(a≠0)的图象向右平移3个单位长度,下列说法正确的是( )
A.对称轴没有改变
B.顶点坐标没有改变
C.开口方向改变
D.函数最值没有改变
11如图,在平面直角坐标系xOy中,抛物线y=ax2+2ax+c与x轴交于A,B两点(点A在点B的左侧),且AB=4,则点A的坐标为( )
A.(1,0) B.(-1,0)
C.(3,0) D.(-3,0)
12(2024·滁州期中)如图,抛物线y=-x2+bx+c与x轴,y轴分别交于A,B两点.若OA=OB,则下列结论成立的是( )
A.4b-c=1 B.b+4c=1
C.4b-c=4 D.4b+c=4
13已知一个二次函数的图象与x轴的交点为(-2,0),(4,0),且顶点在函数y=2x的图象上,则这个函数的解析式是 .
14在平面直角坐标系中,函数y=x2+x-2的图象关于x轴作轴对称变换,变换后所得的抛物线的解析式为 .
15新趋势·模型观念、几何直观
某次数学活动时,数学兴趣小组成员小融拟研究函数y=-(x-2)2+|x-2|+3的图象和性质.
(1)如表是该函数y与自变量x的几组对应值:
x … -2 -1 0 1 2 3 4 5 6 …
y … -1 1.5 m 3.5 3 n 3 1.5 -1 …
其中,m的值为________,n的值为________;
(2)如图,在平面直角坐标系xOy中,描出上表中各组对应值为坐标的点,再根据描出的点,画出该函数图象;
(3)根据函数图象,写出该函数的一条性质:________________________________.
同课章节目录
