青岛版数学七年级上册综合练习:1.4 线段的比较与作法
文档属性
| 名称 | 青岛版数学七年级上册综合练习:1.4 线段的比较与作法 |

|
|
| 格式 | zip | ||
| 文件大小 | 37.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-21 14:53:00 | ||
图片预览


文档简介
1.4 线段的比较与作法
【知能点分类训练】
知能点1 线段大小的比较方法
1.如图1所示,AB=CD,则AC与BD的大小关系是( ).
A.AC>BD B.AC(1) (2)
2.已知线段AB=7厘米,在直线AB上画线段BC=1厘米,那么线段AC=________.
3.如图2所示,已知B,C两点在线段AD上,AC=_____+BC=_____-______,AC+BC-BC=______.
4.如果线段AB=13厘米,MA+MB=17厘米,那么下面说法正确的是( ).
A.M点在线段AB上 B.M点在直线AB上
C.M点在直线AB外 D.M点可能在直线AB上,也可能在直线AB外
知能点2 线段的中点及等分
5.已知点C是线段AB上一点,D是AC的中点,BC=4厘米,DB=7厘米,则AB=______厘米,AC=_______厘米.
6.如图3所示,C和D是线段的三等分点,M是AC的中点,那么CD=______BC,AB=______MC.
(3)
7.如果点B在线段AC上,那么下列表达式中:①AB=AC,②AB=BC,③AC=2AB,④AB+BC=AC.能表示B是线段AC的中点的有( ).
A.1个 B.2个 C.3个 D.4个
8.如图所示,点C在线段AB上,线段AC=6厘米,BC=4厘米,点M,N分别是AC,BC的中点.
(1)求线段MN的长度.
(2)根据(1)的计算过程和结果,设AC+BC=a,其他条件不变,你能猜测出MN的长度吗?请用一句简洁的话表述你发现的规律.
知能点3 线段的基本性质(线段公理)
9.如图所示,由A到B有(1),(2),(3)三条路线,最短的路线选(1)的理由是( ).
A.因为它直 B.两点确定一条直线
C.两点间距离的定义 D.两点之间,线段最短
10.如图所示,一条河流经过A,B两地,为缩短河道,现将河流改道,怎样才能使两地之间河道最短?
( http: / / www.21cnjy.com )
11.如图所示,在△ABC中一定存在下面关系:AB+AC>BC,你能说明原因吗?由此你又能得到什么结论呢?
( http: / / www.21cnjy.com )
12.如图所示,A,B是两个村庄,若要在河边L上修建一个水泵站往两村输水,问水泵站应修在河边的什么位置,才能使铺设的管道最短,并说明理由.
( http: / / www.21cnjy.com )
【综合应用提高】
13.C是线段AB上的中点,D是线段BC上一点,则下列说法不正确的是( ).
A.CD=AC-BD B.CD=AB-BD
C.CD=AD-BC D.CD=BC
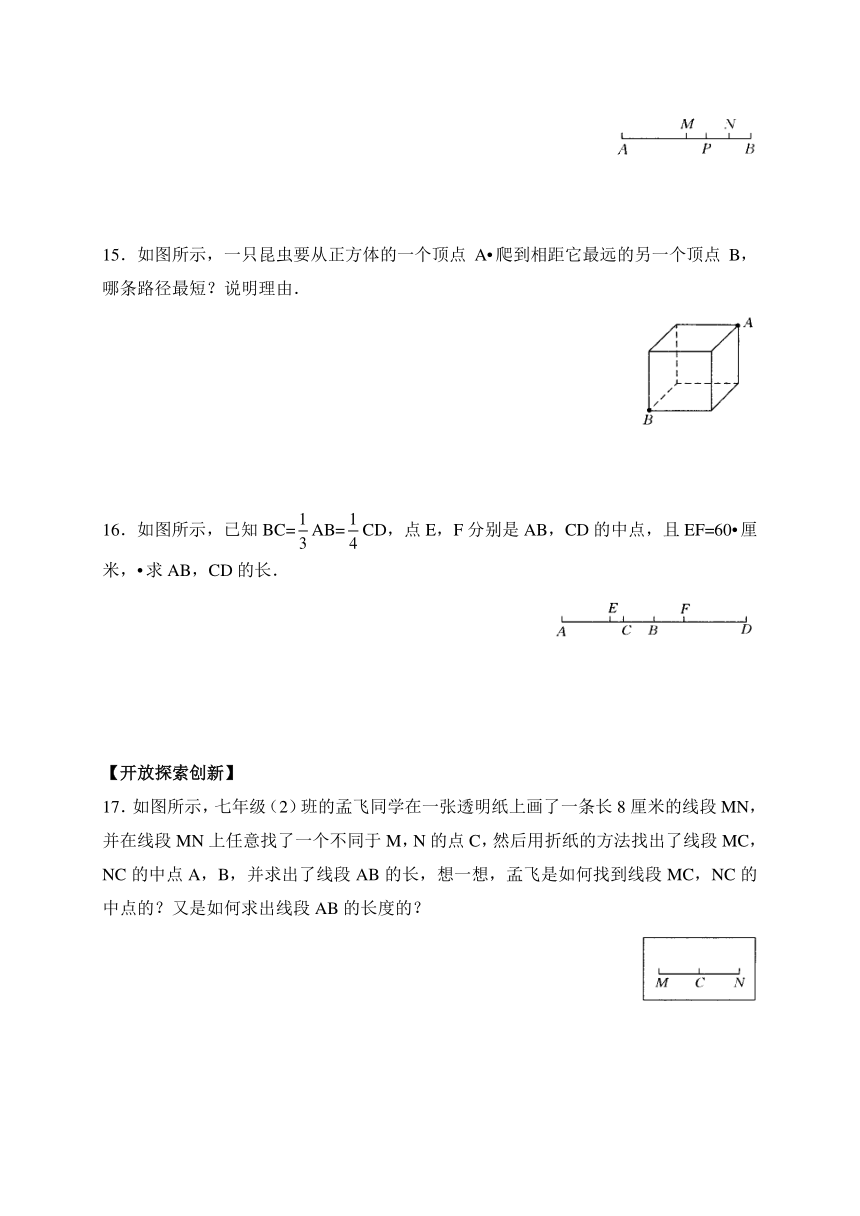
14.如图所示,已知线段AB=80厘米,M为AB的中点,P在MB上,N为PB的中点,且NB=14厘米,求PA的长.
15.如图所示,一只昆虫要从正方体的一个顶点A爬到相距它最远的另一个顶点B,哪条路径最短?说明理由.
( http: / / www.21cnjy.com )
16.如图所示,已知BC=AB=CD,点E,F分别是AB,CD的中点,且EF=60厘米,求AB,CD的长.
【开放探索创新】
17.如图所示,七年级(2)班的孟飞同学 ( http: / / www.21cnjy.com )在一张透明纸上画了一条长8厘米的线段MN,并在线段MN上任意找了一个不同于M,N的点C,然后用折纸的方法找出了线段MC,NC的中点A,B,并求出了线段AB的长,想一想,孟飞是如何找到线段MC,NC的中点的?又是如何求出线段AB的长度的?
【中考真题实战】
18.将一张长方形的纸对折,如图可以得到一 ( http: / / www.21cnjy.com )条折痕,继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到_______条折痕,如果对折n次,可以得到______条折痕.
( http: / / www.21cnjy.com )
19.已知线段AB,C是AB的中点,D是BC的中点,下面等式不正确的是( ).
A.CD=AC-DB B.CD=AD-BC
C.CD=AB-BD D.CD=AB
20.如图所示,从A地到B地有多条道路,一般地,人们会走中间的直路,而不会走其他的曲折的路线,这是因为( ).
( http: / / www.21cnjy.com )
A.两点之间线段最短 B.两直线相交只有一个交点
C.两点确定一条直线 D.垂线段最短
参考答案:
1.C (点拨:∵AB=CD,∴AB+BC=CD+BC,∴AC=BD)
2.8厘米或6厘米 (点拨:分两种情况:①C在线段AB内,②C在线段AB延长线上)
3.AB AD CD AD
4.D 5.10 6 6. 6 7.C (点拨:①②③)
8.解:(1)∵AC=6厘米,BC=4厘米,∴AB=AC+BC=10厘米
又∵点M是AC的中点,点N是BC的中点,
∴MC=AM=AC,CN=BN=BC,
∴MN=MC+CN=AC+BC=(AC+BC)=AB=5厘米.
(2)由(1)中已知AB=10厘米,求出MN=5厘米,分析(1)的推算过程可知MN=AB,故当AB=a时,MN=a,从而得到发现的规律:
线段上任一点把线段分成的两部分的中点间的距离等于原线段长度的一半.
9.D
10.将A,B两点间的曲线河道改为线段.
11.BA+AC与BC可看成由B到C的两条线,一条是折线,即曲线,另一条是直线.
根据:两点之间,线段最短.
结论:三角形两边之和大于第三边.
12.过点A,B作线段AB,与直线L的交点P为所求水泵站的点,因为两点之间,线段最短.
13.D (点拨:如图所示:CD=BC-BD=AC-BD=AB-BD,CD=AD-AC=AD-BC,D不是BC的中点,∴CD≠BC,故选D)
14.解:∵N是BP中点,M是AB中点,
∴PB=2NB=2×14=28(厘米),
∵AM=MB=AB=×80=40(厘米),
∴MP=MB-PB=40-28=12(厘米),
∴PA=AM+MP=40+12=52(厘米).
15.如图将正方体展开,根据“两点之间,线段最短”知,线段AB即为最短路线.
( http: / / www.21cnjy.com )
16.解:设BC=x厘米,由题意得
AB=3x,CD=4x.
∵E,F分别是AB,CD的中点,
∴BE=AB=x,CF=CD=2x,
∴EF=BE+CF-BC= HYPERLINK "http://" x+2x-x.
即x+2x-x=60
解得x=24
∴AB=3x=72(厘米),CD=4x=96(厘米)
答:线段AB长为72厘米,线段CD长为96厘米.
17.解:孟飞同学是将纸对折,使M,C重合,N,C重合,两个折痕与线段的交点就分别是中点A和B;他是根据AB= HYPERLINK "http://" MN,求出AB=4厘米.
18.15 2n-1 19.D 20.A.
【知能点分类训练】
知能点1 线段大小的比较方法
1.如图1所示,AB=CD,则AC与BD的大小关系是( ).
A.AC>BD B.AC
2.已知线段AB=7厘米,在直线AB上画线段BC=1厘米,那么线段AC=________.
3.如图2所示,已知B,C两点在线段AD上,AC=_____+BC=_____-______,AC+BC-BC=______.
4.如果线段AB=13厘米,MA+MB=17厘米,那么下面说法正确的是( ).
A.M点在线段AB上 B.M点在直线AB上
C.M点在直线AB外 D.M点可能在直线AB上,也可能在直线AB外
知能点2 线段的中点及等分
5.已知点C是线段AB上一点,D是AC的中点,BC=4厘米,DB=7厘米,则AB=______厘米,AC=_______厘米.
6.如图3所示,C和D是线段的三等分点,M是AC的中点,那么CD=______BC,AB=______MC.
(3)
7.如果点B在线段AC上,那么下列表达式中:①AB=AC,②AB=BC,③AC=2AB,④AB+BC=AC.能表示B是线段AC的中点的有( ).
A.1个 B.2个 C.3个 D.4个
8.如图所示,点C在线段AB上,线段AC=6厘米,BC=4厘米,点M,N分别是AC,BC的中点.
(1)求线段MN的长度.
(2)根据(1)的计算过程和结果,设AC+BC=a,其他条件不变,你能猜测出MN的长度吗?请用一句简洁的话表述你发现的规律.
知能点3 线段的基本性质(线段公理)
9.如图所示,由A到B有(1),(2),(3)三条路线,最短的路线选(1)的理由是( ).
A.因为它直 B.两点确定一条直线
C.两点间距离的定义 D.两点之间,线段最短
10.如图所示,一条河流经过A,B两地,为缩短河道,现将河流改道,怎样才能使两地之间河道最短?
( http: / / www.21cnjy.com )
11.如图所示,在△ABC中一定存在下面关系:AB+AC>BC,你能说明原因吗?由此你又能得到什么结论呢?
( http: / / www.21cnjy.com )
12.如图所示,A,B是两个村庄,若要在河边L上修建一个水泵站往两村输水,问水泵站应修在河边的什么位置,才能使铺设的管道最短,并说明理由.
( http: / / www.21cnjy.com )
【综合应用提高】
13.C是线段AB上的中点,D是线段BC上一点,则下列说法不正确的是( ).
A.CD=AC-BD B.CD=AB-BD
C.CD=AD-BC D.CD=BC
14.如图所示,已知线段AB=80厘米,M为AB的中点,P在MB上,N为PB的中点,且NB=14厘米,求PA的长.
15.如图所示,一只昆虫要从正方体的一个顶点A爬到相距它最远的另一个顶点B,哪条路径最短?说明理由.
( http: / / www.21cnjy.com )
16.如图所示,已知BC=AB=CD,点E,F分别是AB,CD的中点,且EF=60厘米,求AB,CD的长.
【开放探索创新】
17.如图所示,七年级(2)班的孟飞同学 ( http: / / www.21cnjy.com )在一张透明纸上画了一条长8厘米的线段MN,并在线段MN上任意找了一个不同于M,N的点C,然后用折纸的方法找出了线段MC,NC的中点A,B,并求出了线段AB的长,想一想,孟飞是如何找到线段MC,NC的中点的?又是如何求出线段AB的长度的?
【中考真题实战】
18.将一张长方形的纸对折,如图可以得到一 ( http: / / www.21cnjy.com )条折痕,继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到_______条折痕,如果对折n次,可以得到______条折痕.
( http: / / www.21cnjy.com )
19.已知线段AB,C是AB的中点,D是BC的中点,下面等式不正确的是( ).
A.CD=AC-DB B.CD=AD-BC
C.CD=AB-BD D.CD=AB
20.如图所示,从A地到B地有多条道路,一般地,人们会走中间的直路,而不会走其他的曲折的路线,这是因为( ).
( http: / / www.21cnjy.com )
A.两点之间线段最短 B.两直线相交只有一个交点
C.两点确定一条直线 D.垂线段最短
参考答案:
1.C (点拨:∵AB=CD,∴AB+BC=CD+BC,∴AC=BD)
2.8厘米或6厘米 (点拨:分两种情况:①C在线段AB内,②C在线段AB延长线上)
3.AB AD CD AD
4.D 5.10 6 6. 6 7.C (点拨:①②③)
8.解:(1)∵AC=6厘米,BC=4厘米,∴AB=AC+BC=10厘米
又∵点M是AC的中点,点N是BC的中点,
∴MC=AM=AC,CN=BN=BC,
∴MN=MC+CN=AC+BC=(AC+BC)=AB=5厘米.
(2)由(1)中已知AB=10厘米,求出MN=5厘米,分析(1)的推算过程可知MN=AB,故当AB=a时,MN=a,从而得到发现的规律:
线段上任一点把线段分成的两部分的中点间的距离等于原线段长度的一半.
9.D
10.将A,B两点间的曲线河道改为线段.
11.BA+AC与BC可看成由B到C的两条线,一条是折线,即曲线,另一条是直线.
根据:两点之间,线段最短.
结论:三角形两边之和大于第三边.
12.过点A,B作线段AB,与直线L的交点P为所求水泵站的点,因为两点之间,线段最短.
13.D (点拨:如图所示:CD=BC-BD=AC-BD=AB-BD,CD=AD-AC=AD-BC,D不是BC的中点,∴CD≠BC,故选D)
14.解:∵N是BP中点,M是AB中点,
∴PB=2NB=2×14=28(厘米),
∵AM=MB=AB=×80=40(厘米),
∴MP=MB-PB=40-28=12(厘米),
∴PA=AM+MP=40+12=52(厘米).
15.如图将正方体展开,根据“两点之间,线段最短”知,线段AB即为最短路线.
( http: / / www.21cnjy.com )
16.解:设BC=x厘米,由题意得
AB=3x,CD=4x.
∵E,F分别是AB,CD的中点,
∴BE=AB=x,CF=CD=2x,
∴EF=BE+CF-BC= HYPERLINK "http://" x+2x-x.
即x+2x-x=60
解得x=24
∴AB=3x=72(厘米),CD=4x=96(厘米)
答:线段AB长为72厘米,线段CD长为96厘米.
17.解:孟飞同学是将纸对折,使M,C重合,N,C重合,两个折痕与线段的交点就分别是中点A和B;他是根据AB= HYPERLINK "http://" MN,求出AB=4厘米.
18.15 2n-1 19.D 20.A.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
