苏科版数学七年级上册课件:2.7 有理数的乘方(共19张PPT)
文档属性
| 名称 | 苏科版数学七年级上册课件:2.7 有理数的乘方(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 848.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-21 00:00:00 | ||
图片预览





文档简介
课件19张PPT。2.7 有理数的乘方板块一、感受生活中一类特殊的乘法运算数学实验:折纸活动
【问题1】观察对折的次数与纸的层数的变化,你发现什么规律?
(操作后先独立思考,再同桌交流)
【问题2】你能用算式表示5次对折出来的纸的层数吗?
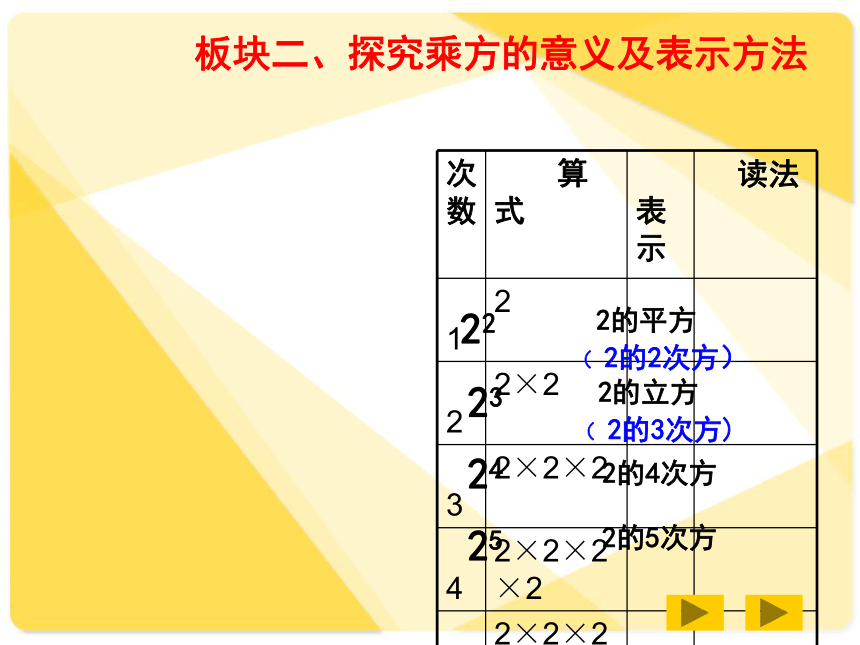
(独立完成后同桌核对)2×2×2×2×2定义:求相同因数的积的运算叫做乘方.回忆:1、边长为5的正方形的面积如何表示?2、棱长为5的正方体的体积如何表示?读作:5的平方。读作:5的立方。5×55×5×5简记作 52简记作 53板块二、探究乘方的意义及表示方法22 2的平方232425 2的立方 2的4次方 2的5次方( 2的2次方)( 2的3次方)板块二、探究乘方的意义及表示方法【问题1】6个3相乘如何表示?8个10相乘如何表示?
(同桌互相说一说)
【问题2】n个2相乘如何表示?n个a相乘又如何表示?
(先写在练习本上再同桌核对)
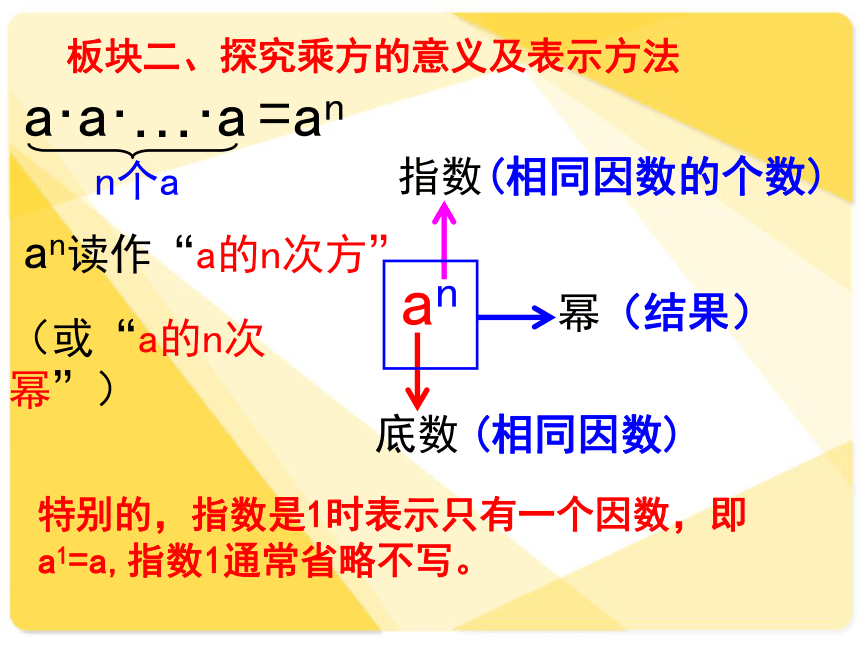
an读作“a的n次方”底数指数幂(结果)a·a·…·a=ann个aan(或“a的n次幂”)(相同因数)(相同因数的个数)板块二、探究乘方的意义及表示方法特别的,指数是1时表示只有一个因数,即 a1=a,指数1通常省略不写。练习巩固: (1)在49中,底数是 ,指数是 ,读作 ,或读作 ;
(2)在(-2)3中,底数是 ,指数是 ,读作 ,或读作 ;
(3)在 中,底数是 ,指数是 ,读作 ,或读作 ;
494的9次方4的9次幂-23-2的3次方-2的3次幂4的4次方的4次幂板块三、探究负数、分数的乘方的表示方法【问题1】-2的4次方如何表示?
(独立写好后小组交流)
【问题2】比较(-2)4与 -24有什么不同?
(小组讨论,组长归纳)
四点不同:
(1)底数不同;(2)运算的意义不同;
(3)读法不同;(4)运算的结果也不同。板块三、探究负数、分数的乘方的表示方法【问题3】你认为 的5次方应该如何表示?练习:-(-3)4读作 ,它表示的意义是 ,
结果是 。注意:负数(分数)的乘方,在书写时一定要把整个负数(分数)用小括号括起来,这也是辨认底数的方法。 -3的4次方的相反数4个-3的乘积的相反数-81板块四、尝试有理数的乘方运算例1.计算:(独立完成后同桌互批)
(1)34 (2)73 (3) (4)08
(5)(-5)2 (6)(-2)5
(7) (8)【问题】从以上练习中,你发现有理数的幂的符号有什么规律?
(先独立思考再小组讨论)结论:
(1)正数的任何次幂都是正数;
(2)0的任何正整数次幂都是0.
(3)负数的奇次幂是负数,负数的偶次幂是正数。板块五、探究有理数的幂的符号规律 想一想:
【问题1】请你找一个正整数,使(-2)n = 2n 成立;板块五、探究有理数的幂的符号规律【问题2】当n为 时,(-2)n = 2n 成立;【问题3】请你找一个正整数,使(-2)n = -2n 成立;【问题4】当n为 时,(-2)n = -2n 成立;
偶数奇数0【问题5】 珠穆朗玛峰是世界的最高峰,它的海拔高度是8848米。
假如能把一张足够大的厚度为0.1毫米的纸连续对折30次,它的的厚度能超过珠穆朗玛峰吗?板块六、乘方运算在生活中的应用折纸 纸的
次数 厚度(毫米) 1 0.1×2 2 0.1×2×2 3 0.1×2×2×2…… 30 0.1×2×2×···×2=0.1×22=0.1×2330个2=0.1×2300.1×230=0.1×1073741824毫米
=107374.1824米>8848米板块六、乘方运算在生活中的应用“乘方”精神:虽然是简简单单的重复,但结果却是惊人的.做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的!感悟:1.掌握有理数的乘方的意义和相关概念;(在表示有理数的乘方时要注意什么?)2.会进行乘方的有关运算;
(运算时要注意什么?)小结与思考3.体会特殊到一般,具体到抽象的数学方法。
判断:(对的画“√”,错的画“×”.)(1) 32 = 3×2 = 6; ( )(2) (-2)3 = (-3)2; ( )(3) -33 = (-3)3; ( )自主检测(4) ; ( )(5) . ( )XX√XX 32 = 3×3=9(-2)3 =-8; (-3)2=9 -24=-2×2×2×2=-16 棋盘上的数学
古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“陛下,就在这个棋盘上放一些米粒吧!第1格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒…,一直到第64格。”“你真傻!就要这么一点米粒?!”国王哈哈大笑,大臣说:“就怕您的国库里没有这么多米!”第1格:1第2格:2第3格:4=2×2第4格:8第5格:16……第64格: ?=2×2×2=2×2×2×263个2=2×2×···×2=22=23=24=263聪明的同学,你能算出总共要多少粒大米呢?拓展延伸
【问题1】观察对折的次数与纸的层数的变化,你发现什么规律?
(操作后先独立思考,再同桌交流)
【问题2】你能用算式表示5次对折出来的纸的层数吗?
(独立完成后同桌核对)2×2×2×2×2定义:求相同因数的积的运算叫做乘方.回忆:1、边长为5的正方形的面积如何表示?2、棱长为5的正方体的体积如何表示?读作:5的平方。读作:5的立方。5×55×5×5简记作 52简记作 53板块二、探究乘方的意义及表示方法22 2的平方232425 2的立方 2的4次方 2的5次方( 2的2次方)( 2的3次方)板块二、探究乘方的意义及表示方法【问题1】6个3相乘如何表示?8个10相乘如何表示?
(同桌互相说一说)
【问题2】n个2相乘如何表示?n个a相乘又如何表示?
(先写在练习本上再同桌核对)
an读作“a的n次方”底数指数幂(结果)a·a·…·a=ann个aan(或“a的n次幂”)(相同因数)(相同因数的个数)板块二、探究乘方的意义及表示方法特别的,指数是1时表示只有一个因数,即 a1=a,指数1通常省略不写。练习巩固: (1)在49中,底数是 ,指数是 ,读作 ,或读作 ;
(2)在(-2)3中,底数是 ,指数是 ,读作 ,或读作 ;
(3)在 中,底数是 ,指数是 ,读作 ,或读作 ;
494的9次方4的9次幂-23-2的3次方-2的3次幂4的4次方的4次幂板块三、探究负数、分数的乘方的表示方法【问题1】-2的4次方如何表示?
(独立写好后小组交流)
【问题2】比较(-2)4与 -24有什么不同?
(小组讨论,组长归纳)
四点不同:
(1)底数不同;(2)运算的意义不同;
(3)读法不同;(4)运算的结果也不同。板块三、探究负数、分数的乘方的表示方法【问题3】你认为 的5次方应该如何表示?练习:-(-3)4读作 ,它表示的意义是 ,
结果是 。注意:负数(分数)的乘方,在书写时一定要把整个负数(分数)用小括号括起来,这也是辨认底数的方法。 -3的4次方的相反数4个-3的乘积的相反数-81板块四、尝试有理数的乘方运算例1.计算:(独立完成后同桌互批)
(1)34 (2)73 (3) (4)08
(5)(-5)2 (6)(-2)5
(7) (8)【问题】从以上练习中,你发现有理数的幂的符号有什么规律?
(先独立思考再小组讨论)结论:
(1)正数的任何次幂都是正数;
(2)0的任何正整数次幂都是0.
(3)负数的奇次幂是负数,负数的偶次幂是正数。板块五、探究有理数的幂的符号规律 想一想:
【问题1】请你找一个正整数,使(-2)n = 2n 成立;板块五、探究有理数的幂的符号规律【问题2】当n为 时,(-2)n = 2n 成立;【问题3】请你找一个正整数,使(-2)n = -2n 成立;【问题4】当n为 时,(-2)n = -2n 成立;
偶数奇数0【问题5】 珠穆朗玛峰是世界的最高峰,它的海拔高度是8848米。
假如能把一张足够大的厚度为0.1毫米的纸连续对折30次,它的的厚度能超过珠穆朗玛峰吗?板块六、乘方运算在生活中的应用折纸 纸的
次数 厚度(毫米) 1 0.1×2 2 0.1×2×2 3 0.1×2×2×2…… 30 0.1×2×2×···×2=0.1×22=0.1×2330个2=0.1×2300.1×230=0.1×1073741824毫米
=107374.1824米>8848米板块六、乘方运算在生活中的应用“乘方”精神:虽然是简简单单的重复,但结果却是惊人的.做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的!感悟:1.掌握有理数的乘方的意义和相关概念;(在表示有理数的乘方时要注意什么?)2.会进行乘方的有关运算;
(运算时要注意什么?)小结与思考3.体会特殊到一般,具体到抽象的数学方法。
判断:(对的画“√”,错的画“×”.)(1) 32 = 3×2 = 6; ( )(2) (-2)3 = (-3)2; ( )(3) -33 = (-3)3; ( )自主检测(4) ; ( )(5) . ( )XX√XX 32 = 3×3=9(-2)3 =-8; (-3)2=9 -24=-2×2×2×2=-16 棋盘上的数学
古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“陛下,就在这个棋盘上放一些米粒吧!第1格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒…,一直到第64格。”“你真傻!就要这么一点米粒?!”国王哈哈大笑,大臣说:“就怕您的国库里没有这么多米!”第1格:1第2格:2第3格:4=2×2第4格:8第5格:16……第64格: ?=2×2×2=2×2×2×263个2=2×2×···×2=22=23=24=263聪明的同学,你能算出总共要多少粒大米呢?拓展延伸
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
