2024-2025学年黑龙江省哈尔滨市香坊区风华中学九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年黑龙江省哈尔滨市香坊区风华中学九年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 167.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-06 14:07:45 | ||
图片预览



文档简介
2024-2025学年黑龙江省哈尔滨市香坊区风华中学九年级(上)开学
数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列方程是一元二次方程的是( )
A. B. C. D.
2.以下列各数为边不能组成直角三角形的一组是( )
A. 、、 B. 、、 C. 、、 D. 、、
3.下列命题中的真命题是( )
A. 有一组对边平行的四边形是平行四边形 B. 有一个角是直角的四边形是矩形
C. 对角线互相垂直平分的四边形是正方形 D. 有一组邻边相等的平行四边形是菱形
4.已知直线,若,,那么该直线不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5.要组织一次篮球联赛,赛制为单循环形式每两队之间都赛一场,计划安排场比赛,则参赛球队的个数是( )
A. 个 B. 个 C. 个 D. 个
6.若关于的一元二次方程有一个根是,则的值是( )
A. B. C. D. 或
7.如图,在平行四边形中,为的中点,延长至点,使,连接交于点,则等于( )
A.
B.
C.
D.
8.如图,正方形中,,是的中点.将沿对折至,延长交于点,则的长是( )
A. B.
C. D.
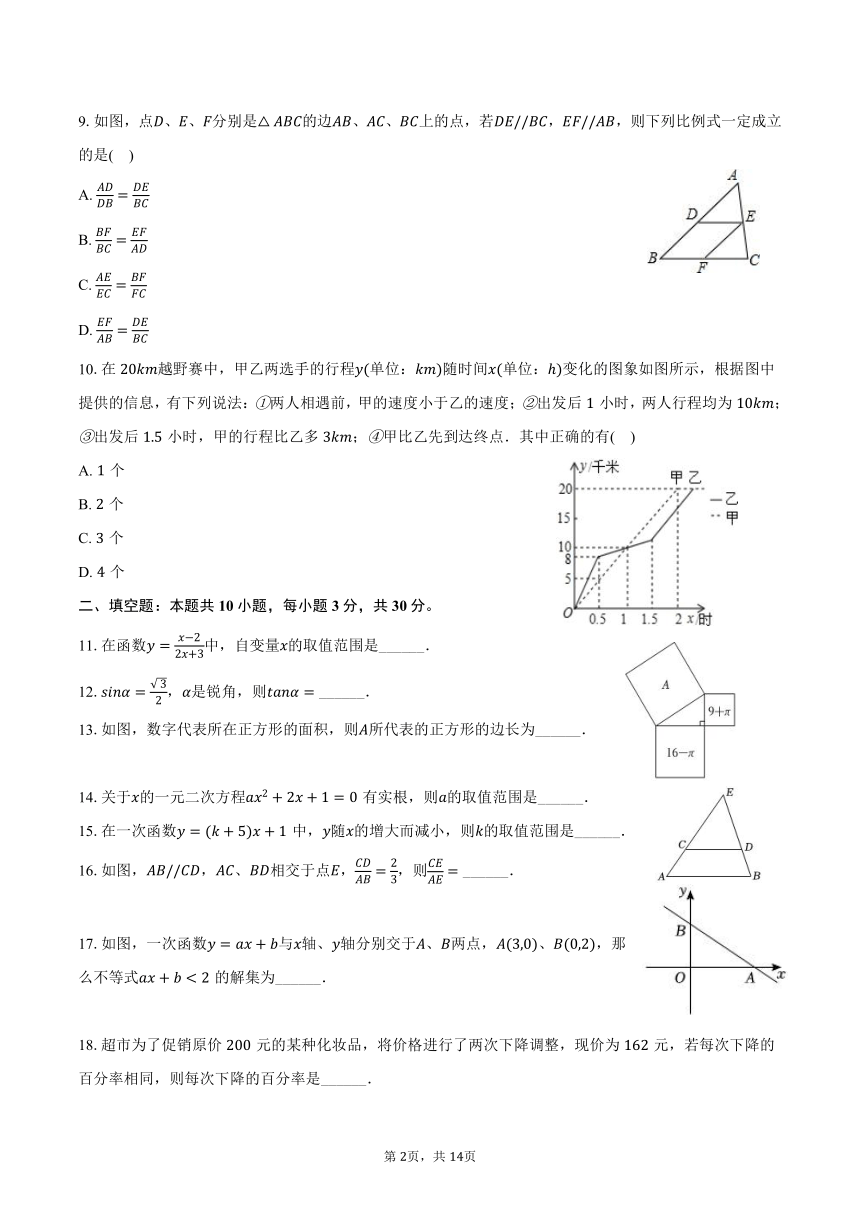
9.如图,点、、分别是的边、、上的点,若,,则下列比例式一定成立的是( )
A.
B.
C.
D.
10.在越野赛中,甲乙两选手的行程单位:随时间单位:变化的图象如图所示,根据图中提供的信息,有下列说法:两人相遇前,甲的速度小于乙的速度;出发后小时,两人行程均为;出发后小时,甲的行程比乙多;甲比乙先到达终点.其中正确的有( )
A. 个
B. 个
C. 个
D. 个
二、填空题:本题共10小题,每小题3分,共30分。
11.在函数中,自变量的取值范围是______.
12.,是锐角,则 ______.
13.如图,数字代表所在正方形的面积,则所代表的正方形的边长为______.
14.关于的一元二次方程有实根,则的取值范围是______.
15.在一次函数中,随的增大而减小,则的取值范围是______.
16.如图,,、相交于点,,则 ______.
17.如图,一次函数与轴、轴分别交于、两点,、,那么不等式的解集为______.
18.超市为了促销原价元的某种化妆品,将价格进行了两次下降调整,现价为元,若每次下降的百分率相同,则每次下降的百分率是______.
19.在矩形中,,,点在直线上,且,则点到矩形对角线所在直线的距离是______.
20.如图,矩形的对角线的垂直平分线交于点,交于点,连接,的面积为,,则的长为______.
三、计算题:本大题共1小题,共7分。
21.先化简,再求值:,其中.
四、解答题:本题共6小题,共53分。解答应写出文字说明,证明过程或演算步骤。
22.本小题分
如图,在的正方形网格中,每个小正方形的边长均为,有线段,点、均在小正方形的顶点上.
以线段为斜边作等腰,画出;
以为对角线作平行四边形,画出平行四边形,并直接写出平行四边形的周长.
23.本小题分
如图,这个图案是世纪我国汉代的赵爽在注解周髀算经时给出的,人们称它为“赵爽弦图”,受这幅图的启发,数学兴趣小组建立了“一线三直角模型”如图,在中,,将线段绕点顺时针旋转得到线段,作交的延长线于点.
如图,通过观察,线段与的数量关系是______;
如图,连接并延长交的延长线于点,若,,求的面积.
24.本小题分
风电项目对于调整能源结构和转变经济发展方式具有重要意义某电力部门在某地安装了一批风力发电机,如图,某校实践活动小组对其中一架风力发电机的塔杆高度进行了测量,图为测量示意图点,,,均在同一平面内,已知斜坡长为米,斜坡的坡角为,在斜坡顶部处测得风力发电机塔杆顶端点的仰角为,坡底与塔杆底的距离米,求该风力发电机塔杆的高度结果精确到个位;参考数据:,,,
25.本小题分
某小区物管中心计划采购,两种花卉用于美化环境已知购买株种花卉和株种花卉共需要元;购买株种花卉和株种花卉共需要元.
求,两种花卉的单价.
该物管中心计划采购,两种花卉共计株,其中采购种花卉的株数不超过种花卉株数的倍,当,两种花卉分别采购多少株时,总费用最少?并求出最少总费用.
26.本小题分
如图,已知四边形中,,,对角线平分,.
求证:.
如图,延长,交于点,过点作,垂足为,过点作交延长线于,,交于求证:.
如图,在的条件下,过点作交延长线于,::,,求的长.
27.本小题分
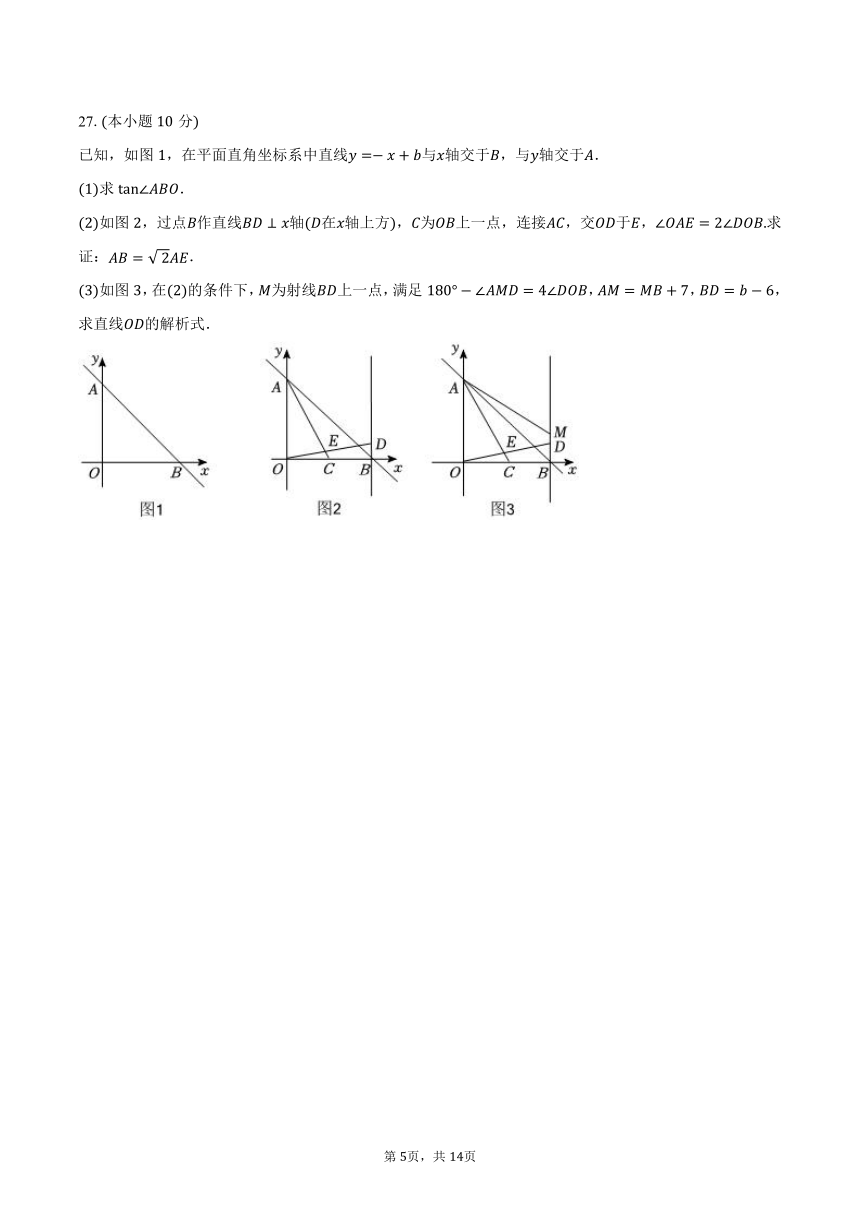
已知,如图,在平面直角坐标系中直线与轴交于,与轴交于.
求.
如图,过点作直线轴在轴上方,为上一点,连接,交于,求证:.
如图,在的条件下,为射线上一点,满足,,,求直线的解析式.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.且
15.
16.
17.
18.
19.或或
20.
21.解:原式,
,
,
当时,原式.
22.解:如图,即为所求.
如图,平行四边形即为所求.
,,
平行四边形的周长为.
23..
线段绕点逆时针旋转得到线段,
,,
,
,
≌,
,,
,,
,,
,
,
,
∽,
,即,
,
,
.
24.解:过点作于点,作于点,
由题意得:,,
在中,
,,
,
,
,
四边形为矩形,
,,
,
,
在中,,
,
,
答:该风力发电机塔杆的高度为.
25.解:设种花卉的单价为元株,种花卉的单价为元株.
由题意得:,
解得:,
答:种花卉的单价为元株,种花卉的单价为元株;
设采购种花卉株,则种花卉株,总费用为元.
由题意得:,
,
解得:,
在中,
,
随的增大而减小,
当时的值最小,
,
此时,
答:当购进种花卉株,种花卉株时,总费用最少,最少费用为元.
26.证明:方法一:如图,作于点,作于点,
平分,
,
在和中,
,
≌,
,
,
,
在四边形中,,
,
.
方法二:如图,在上截取,
平分,
,
,
≌,
,,
,
,
,
,
,
在四边形中,,
,
.
证明:方法一:平分,且,
,
,,
,
,
,
,
由知,
,
,
∽,
,
,
.
方法二:同方法一,先证出,
,
,
.
延长、交于点,
,,
,
由知,
四边形是平行四边形,
,
设,则,
::,
,
,
∽,
,
又,,
≌,
,
,,
∽,
,即,
解得或负值舍去,
,,
在中,,,
,
,
,
在中,,
.
27.解:令,得,
,
令,得,
,
,
;
证明:由知,
,
,
,
设,则,
,
,
,
,
,
;
设,则,
,
,
如图,延长交于点,
轴,
,
,,
,
,
,
,
,
,
,
由知,
,
,
,
,
,
,
过作于点,则,,
,
在中,,
即,
解得或负值舍去,
,,
,
设直线解析式为,
将代入得,
解得,
直线的解析式为
第1页,共1页
数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列方程是一元二次方程的是( )
A. B. C. D.
2.以下列各数为边不能组成直角三角形的一组是( )
A. 、、 B. 、、 C. 、、 D. 、、
3.下列命题中的真命题是( )
A. 有一组对边平行的四边形是平行四边形 B. 有一个角是直角的四边形是矩形
C. 对角线互相垂直平分的四边形是正方形 D. 有一组邻边相等的平行四边形是菱形
4.已知直线,若,,那么该直线不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5.要组织一次篮球联赛,赛制为单循环形式每两队之间都赛一场,计划安排场比赛,则参赛球队的个数是( )
A. 个 B. 个 C. 个 D. 个
6.若关于的一元二次方程有一个根是,则的值是( )
A. B. C. D. 或
7.如图,在平行四边形中,为的中点,延长至点,使,连接交于点,则等于( )
A.
B.
C.
D.
8.如图,正方形中,,是的中点.将沿对折至,延长交于点,则的长是( )
A. B.
C. D.
9.如图,点、、分别是的边、、上的点,若,,则下列比例式一定成立的是( )
A.
B.
C.
D.
10.在越野赛中,甲乙两选手的行程单位:随时间单位:变化的图象如图所示,根据图中提供的信息,有下列说法:两人相遇前,甲的速度小于乙的速度;出发后小时,两人行程均为;出发后小时,甲的行程比乙多;甲比乙先到达终点.其中正确的有( )
A. 个
B. 个
C. 个
D. 个
二、填空题:本题共10小题,每小题3分,共30分。
11.在函数中,自变量的取值范围是______.
12.,是锐角,则 ______.
13.如图,数字代表所在正方形的面积,则所代表的正方形的边长为______.
14.关于的一元二次方程有实根,则的取值范围是______.
15.在一次函数中,随的增大而减小,则的取值范围是______.
16.如图,,、相交于点,,则 ______.
17.如图,一次函数与轴、轴分别交于、两点,、,那么不等式的解集为______.
18.超市为了促销原价元的某种化妆品,将价格进行了两次下降调整,现价为元,若每次下降的百分率相同,则每次下降的百分率是______.
19.在矩形中,,,点在直线上,且,则点到矩形对角线所在直线的距离是______.
20.如图,矩形的对角线的垂直平分线交于点,交于点,连接,的面积为,,则的长为______.
三、计算题:本大题共1小题,共7分。
21.先化简,再求值:,其中.
四、解答题:本题共6小题,共53分。解答应写出文字说明,证明过程或演算步骤。
22.本小题分
如图,在的正方形网格中,每个小正方形的边长均为,有线段,点、均在小正方形的顶点上.
以线段为斜边作等腰,画出;
以为对角线作平行四边形,画出平行四边形,并直接写出平行四边形的周长.
23.本小题分
如图,这个图案是世纪我国汉代的赵爽在注解周髀算经时给出的,人们称它为“赵爽弦图”,受这幅图的启发,数学兴趣小组建立了“一线三直角模型”如图,在中,,将线段绕点顺时针旋转得到线段,作交的延长线于点.
如图,通过观察,线段与的数量关系是______;
如图,连接并延长交的延长线于点,若,,求的面积.
24.本小题分
风电项目对于调整能源结构和转变经济发展方式具有重要意义某电力部门在某地安装了一批风力发电机,如图,某校实践活动小组对其中一架风力发电机的塔杆高度进行了测量,图为测量示意图点,,,均在同一平面内,已知斜坡长为米,斜坡的坡角为,在斜坡顶部处测得风力发电机塔杆顶端点的仰角为,坡底与塔杆底的距离米,求该风力发电机塔杆的高度结果精确到个位;参考数据:,,,
25.本小题分
某小区物管中心计划采购,两种花卉用于美化环境已知购买株种花卉和株种花卉共需要元;购买株种花卉和株种花卉共需要元.
求,两种花卉的单价.
该物管中心计划采购,两种花卉共计株,其中采购种花卉的株数不超过种花卉株数的倍,当,两种花卉分别采购多少株时,总费用最少?并求出最少总费用.
26.本小题分
如图,已知四边形中,,,对角线平分,.
求证:.
如图,延长,交于点,过点作,垂足为,过点作交延长线于,,交于求证:.
如图,在的条件下,过点作交延长线于,::,,求的长.
27.本小题分
已知,如图,在平面直角坐标系中直线与轴交于,与轴交于.
求.
如图,过点作直线轴在轴上方,为上一点,连接,交于,求证:.
如图,在的条件下,为射线上一点,满足,,,求直线的解析式.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.且
15.
16.
17.
18.
19.或或
20.
21.解:原式,
,
,
当时,原式.
22.解:如图,即为所求.
如图,平行四边形即为所求.
,,
平行四边形的周长为.
23..
线段绕点逆时针旋转得到线段,
,,
,
,
≌,
,,
,,
,,
,
,
,
∽,
,即,
,
,
.
24.解:过点作于点,作于点,
由题意得:,,
在中,
,,
,
,
,
四边形为矩形,
,,
,
,
在中,,
,
,
答:该风力发电机塔杆的高度为.
25.解:设种花卉的单价为元株,种花卉的单价为元株.
由题意得:,
解得:,
答:种花卉的单价为元株,种花卉的单价为元株;
设采购种花卉株,则种花卉株,总费用为元.
由题意得:,
,
解得:,
在中,
,
随的增大而减小,
当时的值最小,
,
此时,
答:当购进种花卉株,种花卉株时,总费用最少,最少费用为元.
26.证明:方法一:如图,作于点,作于点,
平分,
,
在和中,
,
≌,
,
,
,
在四边形中,,
,
.
方法二:如图,在上截取,
平分,
,
,
≌,
,,
,
,
,
,
,
在四边形中,,
,
.
证明:方法一:平分,且,
,
,,
,
,
,
,
由知,
,
,
∽,
,
,
.
方法二:同方法一,先证出,
,
,
.
延长、交于点,
,,
,
由知,
四边形是平行四边形,
,
设,则,
::,
,
,
∽,
,
又,,
≌,
,
,,
∽,
,即,
解得或负值舍去,
,,
在中,,,
,
,
,
在中,,
.
27.解:令,得,
,
令,得,
,
,
;
证明:由知,
,
,
,
设,则,
,
,
,
,
,
;
设,则,
,
,
如图,延长交于点,
轴,
,
,,
,
,
,
,
,
,
,
由知,
,
,
,
,
,
,
过作于点,则,,
,
在中,,
即,
解得或负值舍去,
,,
,
设直线解析式为,
将代入得,
解得,
直线的解析式为
第1页,共1页
同课章节目录
