华东师大版数学八年级上册课件:13.3等腰三角形(共12张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册课件:13.3等腰三角形(共12张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 691.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-22 15:03:03 | ||
图片预览



文档简介
课件12张PPT。等腰三角形等
腰
三
角
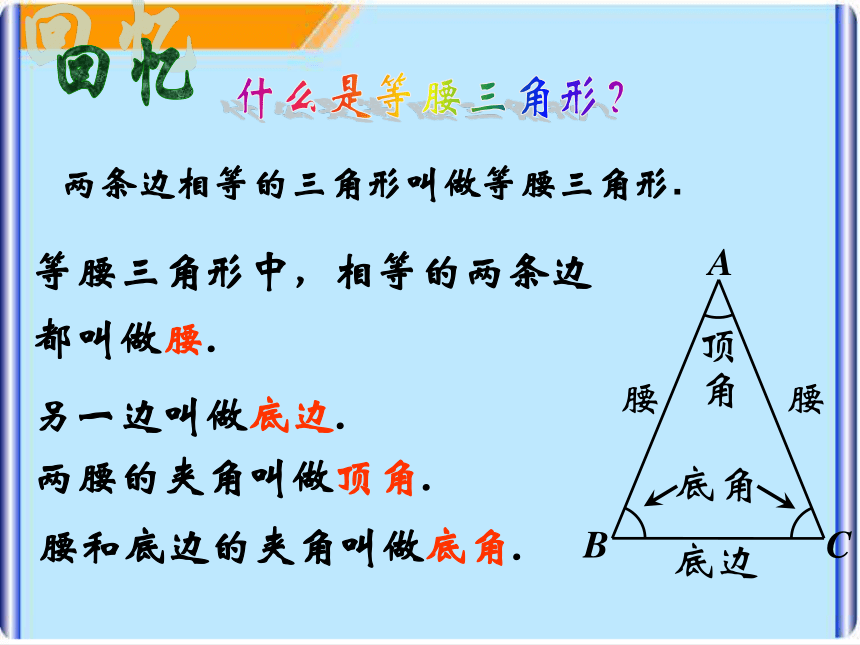
形两条边相等的三角形叫做等腰三角形.等腰三角形中,相等的两条边都叫做腰.底边什么是等腰三角形?两腰的夹角叫做顶角.另一边叫做底边.腰和底边的夹角叫做底角.回忆 做一张等腰三角形的半透明纸片,每个人的等腰三角形的大小和形状可以不一样,如下图,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD.探索研究: 由于AB=AC重合,因此点B与 重合,这样线段BD与CD 也重合,所以∠B=∠C 。点C ABDC性质1.等腰三角形两个底角相等,简称
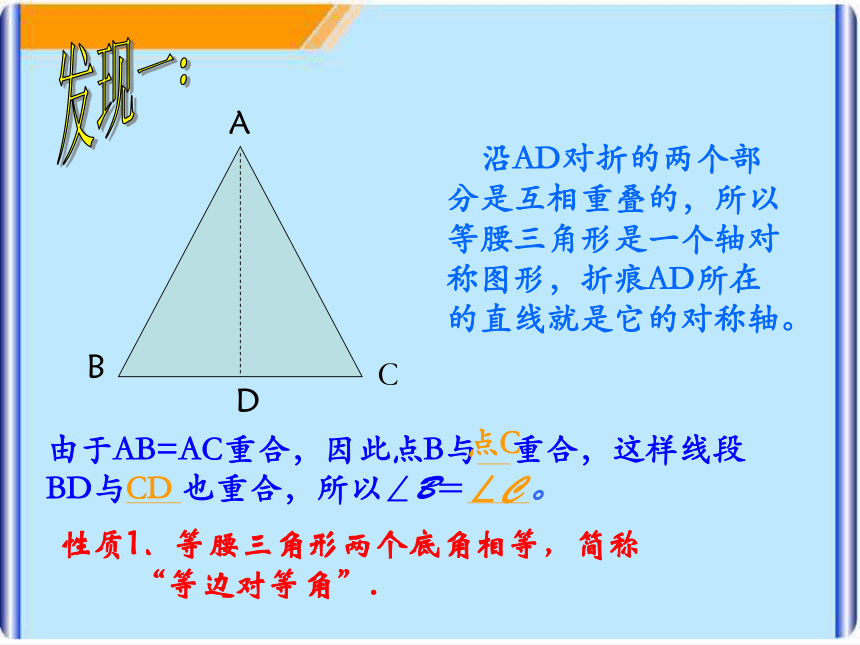
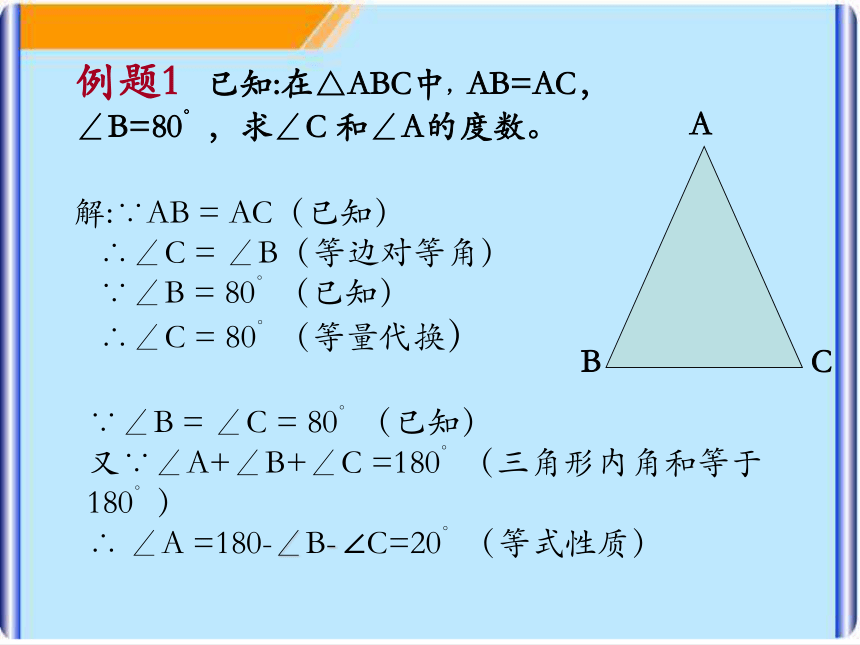
“等边对等角”. 沿AD对折的两个部分是互相重叠的,所以等腰三角形是一个轴对称图形,折痕AD所在的直线就是它的对称轴。发现一:例题1 已知:在△ABC中,AB=AC, ∠B=80°,求∠C 和∠A的度数。ABC 解:∵AB = AC(已知)
∴∠C = ∠B(等边对等角)
∵∠B = 80°(已知)
∴∠C = 80°(等量代换)∵∠B = ∠C = 80°(已知)
又∵∠A+∠B+∠C =180°(三角形内角和等于180°)
∴ ∠A =180-∠B- ∠C=20°(等式性质)ABDC发现二: 由于折痕AD是此等腰三角形的对称轴,我们可以得出:
①BD=CD(AD为底边上的中线)
②∠BAD=∠CAD(AD为顶角的角平分线)
③∠ADB=∠ADC(AD为底边上的高)
所以AD既是底边上的中线,又是顶角的角平分线和底边上的高。
性质2.等腰三角形的顶角平分线、底边上的中线和底边上的高相互重合,简称“三线合一”。
例题2 如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=30°,求(1)∠ADC的度数;(2)∠BAD的度数。ABCD(1)∵ AB=AC,BD=BC(已知)
∴AD⊥BC, ∠BAD= ∠CAD(等腰三角形的三线合一)
∴ ∠ADC = ∠ADB(2)∵ ∠BAD+∠B+∠ADB=180°(三角形内角和等于180°)
∴ ∠BAD=180°-∠B-∠ADB(等式的性质)
=180° -30° -90°=60° 如图,在△ABC中,AB=AC,∠A=56°,CD⊥AB,垂足为D,求∠BCD.练习ABDC解:∵ AB=AC ∴∠B = ∠C
∵∠A+∠B+∠C=180°(三角形的内角和为180°)
∴∠B=∠C=(180°-∠A)÷2=62°
∵CD⊥AB ∴∠ADC=90 °
又∠ADC=∠B+∠BCD
∴∠BCD=∠ADC-∠B=90°-62°=28°小结:等腰三角形的性质
性质1.等腰三角形两个底角相等,简称“等边对等角”.
性质2.等腰三角形的顶角平分线、底边上的中线和底边上的高相互重合,简称“三线合一”。?思考小明练习册上的一个等腰三角形被墨迹污染了,只有它的底边AB和∠B还保留着。你怎样画出练习册上原来的等腰三角形形状呢?AB谢谢!
腰
三
角
形两条边相等的三角形叫做等腰三角形.等腰三角形中,相等的两条边都叫做腰.底边什么是等腰三角形?两腰的夹角叫做顶角.另一边叫做底边.腰和底边的夹角叫做底角.回忆 做一张等腰三角形的半透明纸片,每个人的等腰三角形的大小和形状可以不一样,如下图,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD.探索研究: 由于AB=AC重合,因此点B与 重合,这样线段BD与CD 也重合,所以∠B=∠C 。点C ABDC性质1.等腰三角形两个底角相等,简称
“等边对等角”. 沿AD对折的两个部分是互相重叠的,所以等腰三角形是一个轴对称图形,折痕AD所在的直线就是它的对称轴。发现一:例题1 已知:在△ABC中,AB=AC, ∠B=80°,求∠C 和∠A的度数。ABC 解:∵AB = AC(已知)
∴∠C = ∠B(等边对等角)
∵∠B = 80°(已知)
∴∠C = 80°(等量代换)∵∠B = ∠C = 80°(已知)
又∵∠A+∠B+∠C =180°(三角形内角和等于180°)
∴ ∠A =180-∠B- ∠C=20°(等式性质)ABDC发现二: 由于折痕AD是此等腰三角形的对称轴,我们可以得出:
①BD=CD(AD为底边上的中线)
②∠BAD=∠CAD(AD为顶角的角平分线)
③∠ADB=∠ADC(AD为底边上的高)
所以AD既是底边上的中线,又是顶角的角平分线和底边上的高。
性质2.等腰三角形的顶角平分线、底边上的中线和底边上的高相互重合,简称“三线合一”。
例题2 如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=30°,求(1)∠ADC的度数;(2)∠BAD的度数。ABCD(1)∵ AB=AC,BD=BC(已知)
∴AD⊥BC, ∠BAD= ∠CAD(等腰三角形的三线合一)
∴ ∠ADC = ∠ADB(2)∵ ∠BAD+∠B+∠ADB=180°(三角形内角和等于180°)
∴ ∠BAD=180°-∠B-∠ADB(等式的性质)
=180° -30° -90°=60° 如图,在△ABC中,AB=AC,∠A=56°,CD⊥AB,垂足为D,求∠BCD.练习ABDC解:∵ AB=AC ∴∠B = ∠C
∵∠A+∠B+∠C=180°(三角形的内角和为180°)
∴∠B=∠C=(180°-∠A)÷2=62°
∵CD⊥AB ∴∠ADC=90 °
又∠ADC=∠B+∠BCD
∴∠BCD=∠ADC-∠B=90°-62°=28°小结:等腰三角形的性质
性质1.等腰三角形两个底角相等,简称“等边对等角”.
性质2.等腰三角形的顶角平分线、底边上的中线和底边上的高相互重合,简称“三线合一”。?思考小明练习册上的一个等腰三角形被墨迹污染了,只有它的底边AB和∠B还保留着。你怎样画出练习册上原来的等腰三角形形状呢?AB谢谢!
