华东师大版数学八年级上册课件:14.1《勾股定理》(共21张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册课件:14.1《勾股定理》(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-22 00:00:00 | ||
图片预览



文档简介
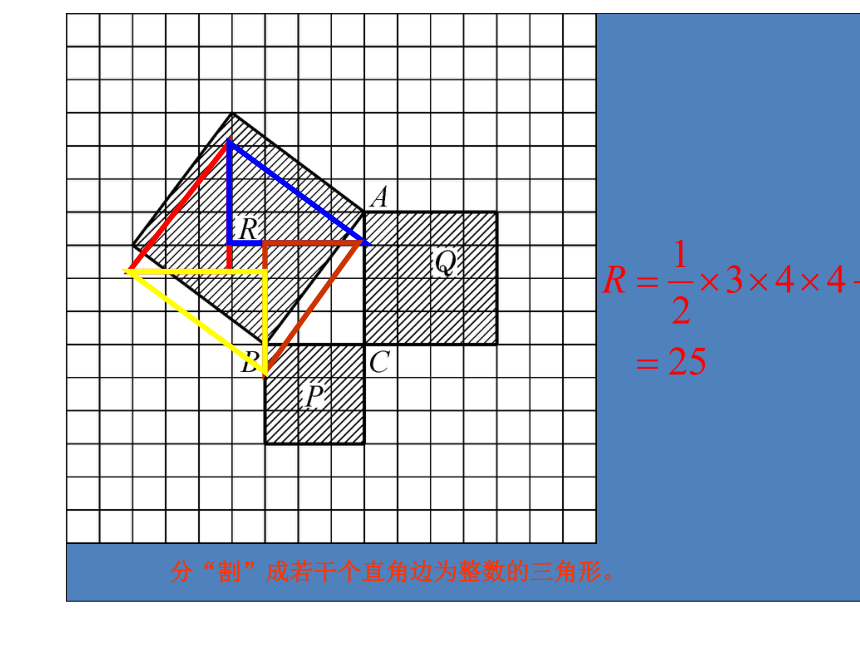
课件21张PPT。14.1勾股定理探索三正方形P的面积= 平方厘米;
正方形Q的面积= 平方厘米;
正方形R的面积= 平方厘米.
正方形P、 Q、 R的面积之间的关系是 .
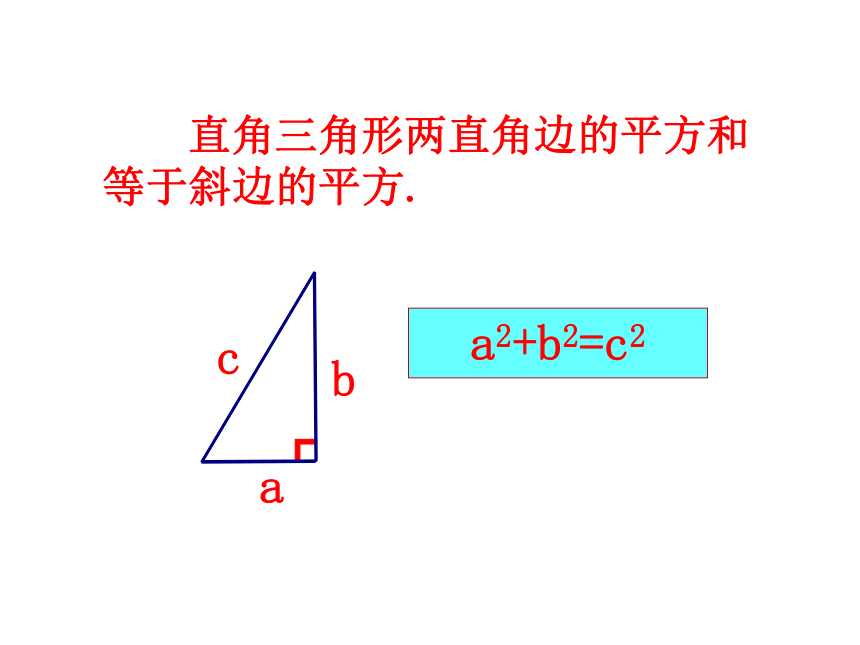
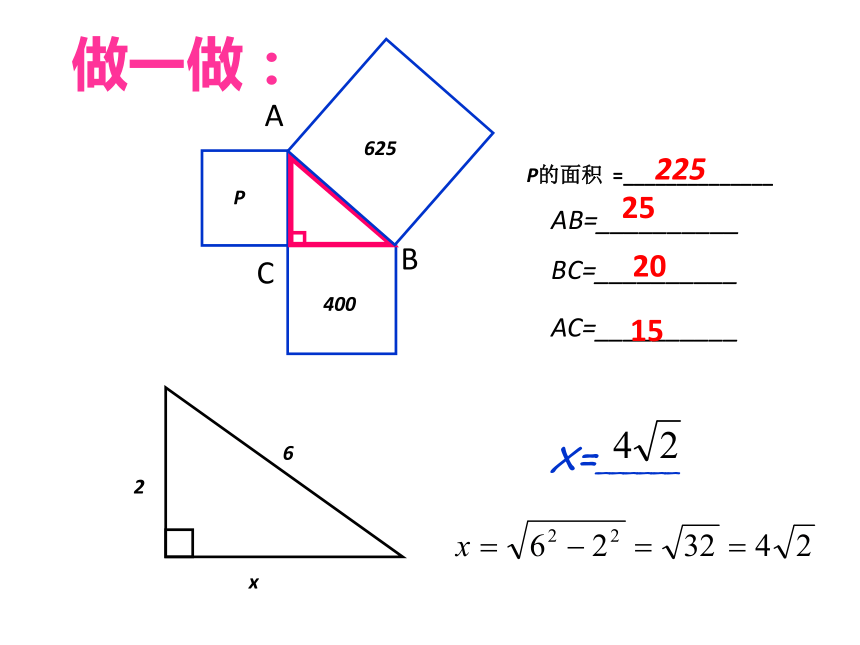
直角三角形ABC的三边的长度之间存在关系 .(每一小方格表示1平方厘米)91625P+ Q= RAC2+BC2=AB2在一般的直角三角形中,两直角边的平方和等于斜边的平方也成立! 分“割”成若干个直角边为整数的三角形。概 括 对于任意的直角三角形,如果它的两条直角边分别为a、 b,斜边为c,那么一定有a2+b2=c2。勾股定理揭示了直角三角形三边之间的关系 勾股定理:abc直角三角形两直角边的平方和等于斜边的平方┏a2+b2=c2acb 直角三角形两直角边的平方和等于斜边的平方.做一做: P62540026xP的面积 =______________X=______225BACAB=__________AC=__________BC=__________251520
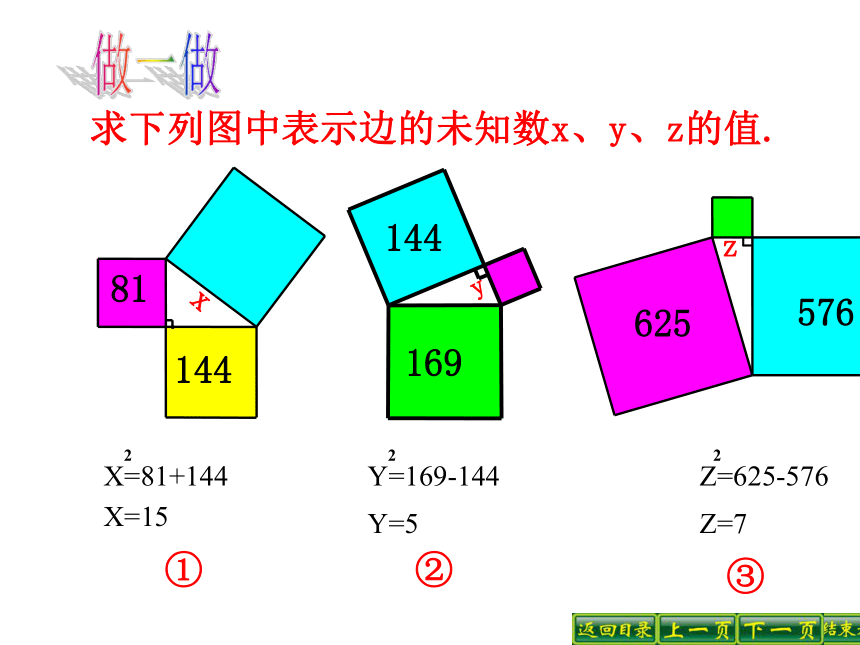
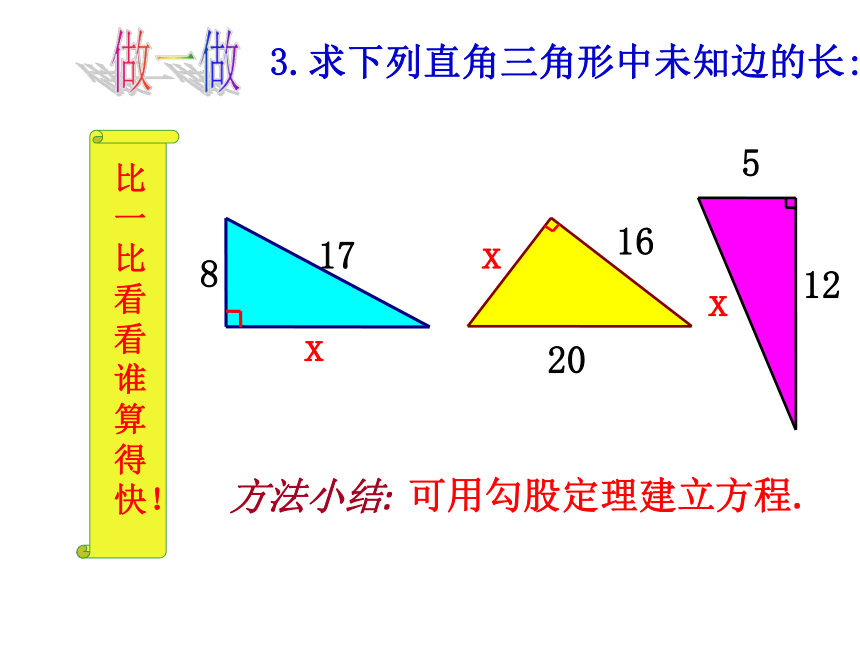
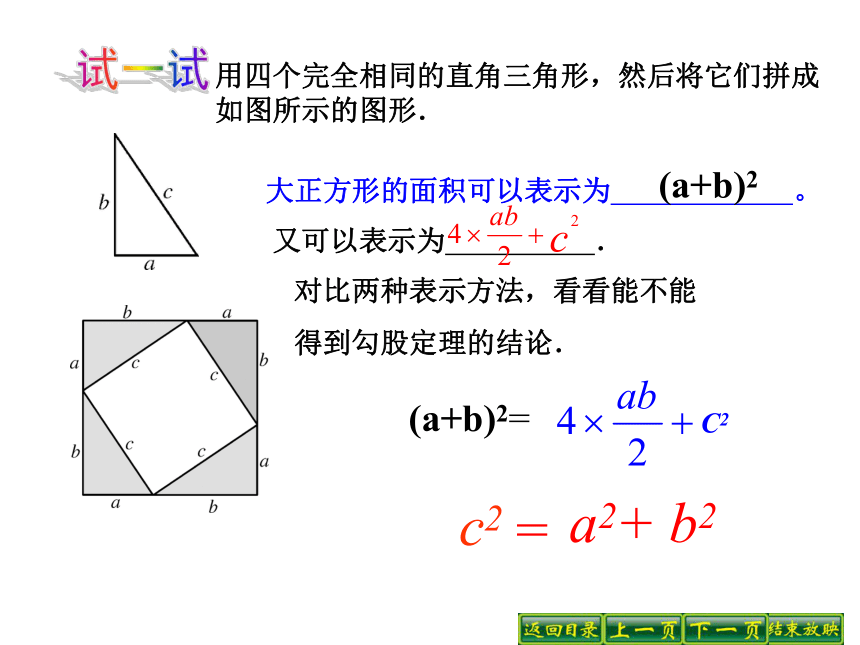
求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做X=81+1442Y=169-144Z=625-57622X=15Y=5Z=7结论:S1+S2+S3+S4=S5+S6=S7比一比看看谁算得快!3.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x做一做试一试用四个完全相同的直角三角形,然后将它们拼成如图所示的图形.大正方形的面积可以表示为 。又可以表示为 .对比两种表示方法,看看能不能
得到勾股定理的结论.(a+b)2试一试用四个完全相同的直角三角形,还可以拼成如图所示的图形.大正方形的面积可以表示为 。又可以表示为 .对比两种表示方法,看看能不能得到勾股定理的结论.= 读一读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的. 弦股勾图1-1 这是1700多年前中国古代数学家赵爽用来证明勾股定理的弦图. 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。┏a2+b2=c2acb 直角三角形两直角边的平方和等于斜边的平方.勾股弦 勾股定理(毕达哥拉斯定理) 如图,为了求出位于湖两岸的两点A、 B之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?如图14.1.9,在直角三角形ABC中,
AC=160米, BC=128米,
根据勾股定理可得
AB=
=
=96(米).
答: 从点A穿过湖到点B有96米.解例如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?9m24m1. 如图,小方格都是边长为1的正方形,求四边形ABCD的面积与周长.练习2. 假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A到宝藏埋藏点B的直线距离是多少千米?课堂小结
勾股定理直角三角形两直角边的平方和等于斜边的平方再见
正方形Q的面积= 平方厘米;
正方形R的面积= 平方厘米.
正方形P、 Q、 R的面积之间的关系是 .
直角三角形ABC的三边的长度之间存在关系 .(每一小方格表示1平方厘米)91625P+ Q= RAC2+BC2=AB2在一般的直角三角形中,两直角边的平方和等于斜边的平方也成立! 分“割”成若干个直角边为整数的三角形。概 括 对于任意的直角三角形,如果它的两条直角边分别为a、 b,斜边为c,那么一定有a2+b2=c2。勾股定理揭示了直角三角形三边之间的关系 勾股定理:abc直角三角形两直角边的平方和等于斜边的平方┏a2+b2=c2acb 直角三角形两直角边的平方和等于斜边的平方.做一做: P62540026xP的面积 =______________X=______225BACAB=__________AC=__________BC=__________251520
求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做X=81+1442Y=169-144Z=625-57622X=15Y=5Z=7结论:S1+S2+S3+S4=S5+S6=S7比一比看看谁算得快!3.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x做一做试一试用四个完全相同的直角三角形,然后将它们拼成如图所示的图形.大正方形的面积可以表示为 。又可以表示为 .对比两种表示方法,看看能不能
得到勾股定理的结论.(a+b)2试一试用四个完全相同的直角三角形,还可以拼成如图所示的图形.大正方形的面积可以表示为 。又可以表示为 .对比两种表示方法,看看能不能得到勾股定理的结论.= 读一读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的. 弦股勾图1-1 这是1700多年前中国古代数学家赵爽用来证明勾股定理的弦图. 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。┏a2+b2=c2acb 直角三角形两直角边的平方和等于斜边的平方.勾股弦 勾股定理(毕达哥拉斯定理) 如图,为了求出位于湖两岸的两点A、 B之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?如图14.1.9,在直角三角形ABC中,
AC=160米, BC=128米,
根据勾股定理可得
AB=
=
=96(米).
答: 从点A穿过湖到点B有96米.解例如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?9m24m1. 如图,小方格都是边长为1的正方形,求四边形ABCD的面积与周长.练习2. 假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A到宝藏埋藏点B的直线距离是多少千米?课堂小结
勾股定理直角三角形两直角边的平方和等于斜边的平方再见
