15.3 等腰三角形第2课时等边三角形的性质课件2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 15.3 等腰三角形第2课时等边三角形的性质课件2024-2025学年度八年级上册沪科版数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 305.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-09 11:46:04 | ||
图片预览





文档简介
(共14张PPT)
沪科版
15.3.2 等边三角形的性质
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.了解等边三角形的性质,掌握等边三角形的性质定理及推论,会用定理及推论解决简单问题;
2.通过观察、操作、想象、推理和交流活动,理解等边三角形“三线合一”等有关性质,提高几何推理意识.
学习目标
重点
难点
新课引入
三角形都有什么性质?
内角和180°
两边之和大于第三边,两边之差小于第三边
三角形是怎么分类的?
按角分:锐角三角形、直角三角形、钝角三角形
按边分:任意三角形、等腰三角形、等边三角形
什么是等边三角形?
定义:三边都相等的三角形是等腰三角形.
等边三角形除了三边相等,还有什么性质呢?
A
B
C
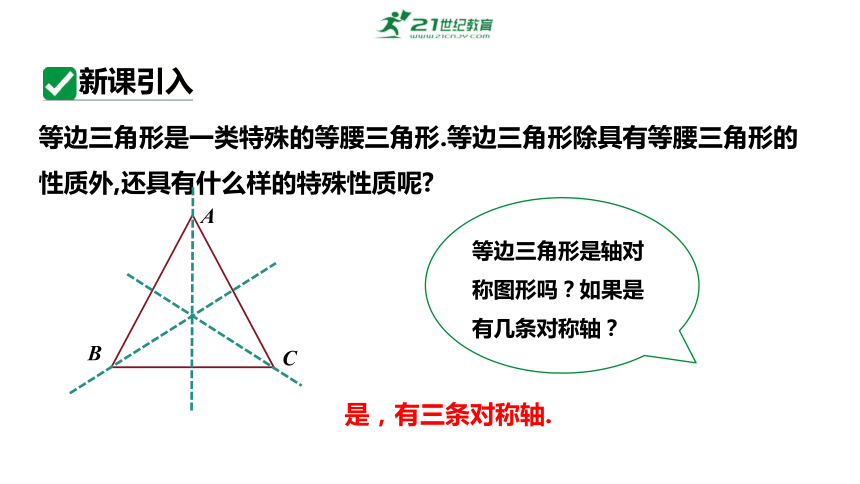
等边三角形是一类特殊的等腰三角形.等边三角形除具有等腰三角形的性质外,还具有什么样的特殊性质呢
等边三角形是轴对称图形吗?如果是有几条对称轴?
新课引入
A
B
C
是,有三条对称轴.
推论 等边三角形三个内角相等,每一个内角都等于60°.
这个推论可以直接根据等腰三角形定理1得到.
因为 AB=BC= CA,
所以∠A=∠B=∠C
由三角形三个内和等于180°
得∠A=∠B=∠C=60°
思考:等边三角形有“三线合一”的性质吗
A
B
C
新知学习
A
B
C
总结:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
三条对称轴
例1 △ABC为正三角形,点M是BC边上一点,点N是CA边上一点,且BM=CN,BN与AM相交于Q点,∠BQM 等于多少度?
解:∵△ABC为正三角形,
∴∠ABC=∠C=∠BAC=60°,AB=BC.
又∵BM=CN,
∴△AMB≌△BCN(SAS),
∴∠BAM=∠CBN,
∴∠BQM=∠ABQ+∠BAM
=∠ABQ+∠CBN=∠ABC=60°.
随堂练习
1. 如图15.3-4,在等边三角形ABC 中,BC = 8,过BC 边上一点P,作∠ DPE = 60°,分别与边AB,AC 相交于点D 与点E.
(1)在图中找出与∠ EPC 始终相等的角,并说明理由.
(2)若△ PDE 为等边三角形,
求BD+CE 的值.
(1)在图中找出与∠ EPC 始终相等的角,并说明理由.
解:∠ BDP= ∠ EPC,理由如下:
∵△ ABC 为等边三角形,∴∠ B=60° .
∵∠ DPE=60°,∴∠ DPE= ∠ B.
∵∠ DPC 是△ BDP 的外角,
∴∠ DPE+ ∠ EPC= ∠ B+ ∠ BDP,
∴∠ EPC= ∠ BDP.
(2)若△ PDE 为等边三角形,求BD+CE 的值.
解:∵△ PDE 为等边三角形,∴ PD=PE.
在△ BDP 和△ CPE 中,
∠ B = ∠ C ,
∠ BDP= ∠ CPE,
PD=EP,
∴△ BDP ≌△ CPE,(AAS)
∴ BD=CP,BP=CE,
∴ BD+CE=CP+BP=BC=8.
2.如图,等边三角形ABC 的边长为3,D 是AC 的中点,点E 在BC 的延长线上,若DE=DB,求CE 的长.
解: ∵△ ABC 是等边三角形,D 是AC 的中点,
∴∠ ABC= ∠ ACB=60°,∠ DBE=
∠ ABC=30° .
又∵ DE=DB,∴∠ E= ∠ DBE=30° .
∵∠ ACB= ∠ CDE+ ∠ E,
∴∠ CDE= ∠ ACB- ∠ E=30° .
∴∠ CDE= ∠ E.
等边三角形
的性质
①等边三角形三个内角相等,每一个内角都等于60°.
②等边三角形是轴对称图形,它有3 条对称轴.
③各边上的高、中线、对应的角平分线重合,
且长度相等.有“三线合一“的性质.
课堂小结
沪科版
15.3.2 等边三角形的性质
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.了解等边三角形的性质,掌握等边三角形的性质定理及推论,会用定理及推论解决简单问题;
2.通过观察、操作、想象、推理和交流活动,理解等边三角形“三线合一”等有关性质,提高几何推理意识.
学习目标
重点
难点
新课引入
三角形都有什么性质?
内角和180°
两边之和大于第三边,两边之差小于第三边
三角形是怎么分类的?
按角分:锐角三角形、直角三角形、钝角三角形
按边分:任意三角形、等腰三角形、等边三角形
什么是等边三角形?
定义:三边都相等的三角形是等腰三角形.
等边三角形除了三边相等,还有什么性质呢?
A
B
C
等边三角形是一类特殊的等腰三角形.等边三角形除具有等腰三角形的性质外,还具有什么样的特殊性质呢
等边三角形是轴对称图形吗?如果是有几条对称轴?
新课引入
A
B
C
是,有三条对称轴.
推论 等边三角形三个内角相等,每一个内角都等于60°.
这个推论可以直接根据等腰三角形定理1得到.
因为 AB=BC= CA,
所以∠A=∠B=∠C
由三角形三个内和等于180°
得∠A=∠B=∠C=60°
思考:等边三角形有“三线合一”的性质吗
A
B
C
新知学习
A
B
C
总结:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
三条对称轴
例1 △ABC为正三角形,点M是BC边上一点,点N是CA边上一点,且BM=CN,BN与AM相交于Q点,∠BQM 等于多少度?
解:∵△ABC为正三角形,
∴∠ABC=∠C=∠BAC=60°,AB=BC.
又∵BM=CN,
∴△AMB≌△BCN(SAS),
∴∠BAM=∠CBN,
∴∠BQM=∠ABQ+∠BAM
=∠ABQ+∠CBN=∠ABC=60°.
随堂练习
1. 如图15.3-4,在等边三角形ABC 中,BC = 8,过BC 边上一点P,作∠ DPE = 60°,分别与边AB,AC 相交于点D 与点E.
(1)在图中找出与∠ EPC 始终相等的角,并说明理由.
(2)若△ PDE 为等边三角形,
求BD+CE 的值.
(1)在图中找出与∠ EPC 始终相等的角,并说明理由.
解:∠ BDP= ∠ EPC,理由如下:
∵△ ABC 为等边三角形,∴∠ B=60° .
∵∠ DPE=60°,∴∠ DPE= ∠ B.
∵∠ DPC 是△ BDP 的外角,
∴∠ DPE+ ∠ EPC= ∠ B+ ∠ BDP,
∴∠ EPC= ∠ BDP.
(2)若△ PDE 为等边三角形,求BD+CE 的值.
解:∵△ PDE 为等边三角形,∴ PD=PE.
在△ BDP 和△ CPE 中,
∠ B = ∠ C ,
∠ BDP= ∠ CPE,
PD=EP,
∴△ BDP ≌△ CPE,(AAS)
∴ BD=CP,BP=CE,
∴ BD+CE=CP+BP=BC=8.
2.如图,等边三角形ABC 的边长为3,D 是AC 的中点,点E 在BC 的延长线上,若DE=DB,求CE 的长.
解: ∵△ ABC 是等边三角形,D 是AC 的中点,
∴∠ ABC= ∠ ACB=60°,∠ DBE=
∠ ABC=30° .
又∵ DE=DB,∴∠ E= ∠ DBE=30° .
∵∠ ACB= ∠ CDE+ ∠ E,
∴∠ CDE= ∠ ACB- ∠ E=30° .
∴∠ CDE= ∠ E.
等边三角形
的性质
①等边三角形三个内角相等,每一个内角都等于60°.
②等边三角形是轴对称图形,它有3 条对称轴.
③各边上的高、中线、对应的角平分线重合,
且长度相等.有“三线合一“的性质.
课堂小结
