15.3等腰三角形第3课时等腰三角形的判定课件2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 15.3等腰三角形第3课时等腰三角形的判定课件2024-2025学年度八年级上册沪科版数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 350.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-09 11:48:18 | ||
图片预览







文档简介
(共22张PPT)
沪科版
15.3.3 等腰三角形的判定
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.领会等腰三角形、等边三角形的判定方法,培养合情推理的能力;
2.能够运用等腰三角形与等边三角形判定方法解答相关问题.
3.探索含30°角的直角三角形的性质.
学习目标
重点
难点
说出等腰三角形的性质
定理1 等腰三角形两个底角相等,简称“等边对等角”.
定理2 等腰三角形顶角的平分线垂直平分底边.
等腰三角形的两个底角相等,反过来的命题是否是真命题呢?请与你的同学研究讨论后作出判断.
一 等腰三角形的判定
新课引入
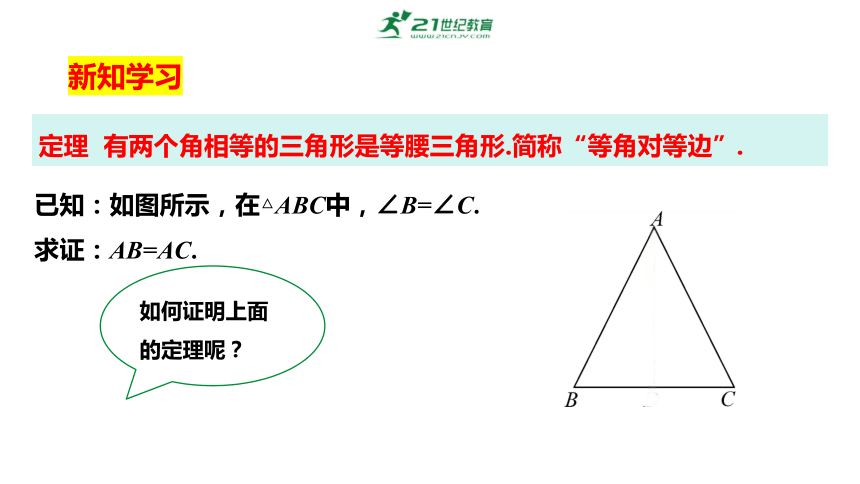
定理 有两个角相等的三角形是等腰三角形.简称“等角对等边”.
如何证明上面的定理呢?
已知:如图所示,在△ABC中,∠B=∠C.
求证:AB=AC.
新知学习
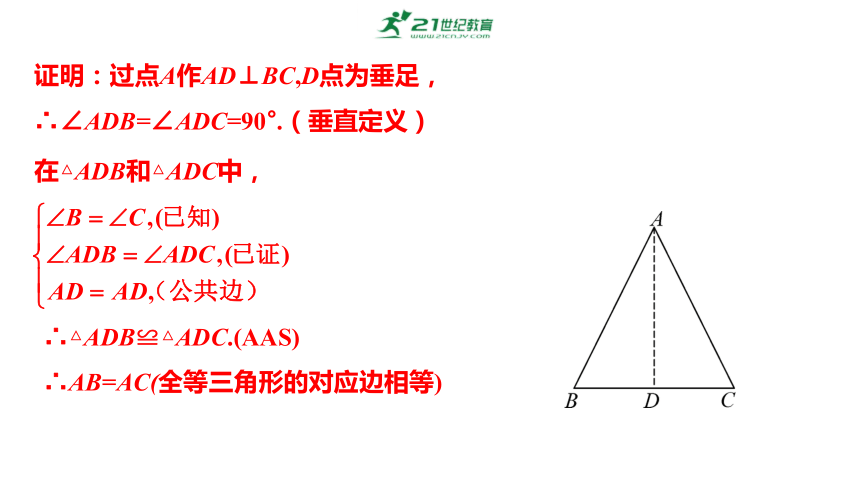
证明:过点A作AD⊥BC,D点为垂足,
∴∠ADB=∠ADC=90°.(垂直定义)
在△ADB和△ADC中,
∴△ADB≌△ADC.(AAS)
∴AB=AC(全等三角形的对应边相等)
这个定理叫做等腰三角形的判定定理,它是判断一个三角形是否为等腰三角形的重要依据.
通过该定理是否能得到其他推论?
注意:不能将等腰三角形的判定定理写成“如果一个三角形两个底角相等,那么它的两腰也相等”,因为在没有判断出三角形为等腰三角形前,不能使用“腰”、“底角”这类等腰三角形专用词语名称
推论1 三个角都相等的三角形是等边三角形.
推论2 有一个角是60°的等腰三角形是等边三角形.
你能对顶角是60°和底角是60°两种情况分类讨论吗?
二 等边三角形的判定
①顶角是60°
证:∵∠O=60°
∴∠A+∠B=120°.
∵△AOB是等腰三角形
∴∠A=∠B=∠O=60°
∴△AOB是等边三角形
②底角是60°
证:∵∠A=60°,且△AOB是等腰三角形
∴∠A=∠B=60°.
∴∠O=180°-∠A-∠B=60°
∴∠A=∠B=∠O=60°
∴△AOB是等边三角形
例1 已知:如图,AD∥BC,BD平分∠ABC.求证:AB=AD
B
A
D
C
证明:∵ AD∥BC,
∴∠ADB=∠DBC.
∵ BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD.
总结:角平分线+平行可得等腰三角形
例2 如图,一艘船从A处出发,以每时10n mile(海里)的速度向正北
航行,从A处测得一礁石C在北偏西30°的方向上.如果这艘船上午8:00从A处出发,10:00到达B处,从B处测得礁石C在北偏西60°的方向上.
(1)画出礁石C的位置;
(2)求从B处到礁石C的距离.
解:(1)以B为顶点,向北偏西60°作角,这角一边与AC交于点C,则点C为礁石所在地.
(2)∵∠ACB= 60°-30°=30°,(三角形的外角性质)
又∵∠BAC= 30°,∴∠BCA=∠BAC.
∴BC=BA.
∵BA=10×(10-8)=20(n mile)
∴BC=20(n mile).
即从 B处到礁石C的距离是20n mile.
1.如图,在△ABD中,C是BD上的一点,且AC⊥BD,AC=BC=CD.求证:
(1)△ABD是等腰三角形.
(2)求∠BAD的度数.
(1)证明:∵AC⊥BD,
∴∠ACB=∠ACD=90°,
又AC=BC=CD,
∴△ABC≌△ADC(SAS),
∴AB=AD,即△ABD是等腰三角形.
随堂练习
(2)由(1)可知,AB=AD,
∴∠B=∠D,又AC=BC=CD,
∴∠B=∠BAC,∠D=∠DAC.
在△ABD中,∠B+∠BAC+∠DAC+∠D=180°,
∴2(∠BAC+∠DAC)=180°,
∴∠BAC+∠DAC=90°,
∴∠BAD=∠BAC+∠DAC=90°.
2.如图,等边△ABC中,D、E、F分别是各边上的一点,且AD=BE=CF.
求证:△DEF是等边三角形.
证明:∵△ABC为等边三角形,且AD=BE=CF
∴AF=BD=CE,
又∵∠A=∠B=∠C=60°,
∴△ADF≌△BED≌△CFE(SAS),
∴DF=ED=FE,
∴△DEF是一个等边三角形.
3.如图,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于点F,试判断△AFC的形状,并说明理由.
解题思路:
1.证明△ABD≌△CBE(AAS)
2.全等三角形性质:对应边相等
(即为BA=BC)
3.等腰三角形性质:等边对等角
(即∠BAC=∠BCA)
4.再证明∠FAC=∠ACF.
4. 已知:如图15.3-13,△ ABC,△ CDE都是等边三角形,AD,BE 相交于点O,点M,N 分别是线段AD,BE 的中点.
(1)求证:AD=BE;
(2)求∠ DOE 的度数;
(3)求证:△ MNC 是等边三角形.
(1)求证:AD=BE;
证明:∵△ ABC,△ CDE 都是等边三角形,
∴ AC=BC,CD=CE,∠ ACB= ∠ DCE=60°,
∴∠ ACB+ ∠ BCD= ∠ DCE+ ∠ BCD,
∴∠ ACD= ∠ BCE.
在△ ACD 和△ BCE 中, AC=BC,
∠ ACD= ∠ BCE,
CD=CE,
∴△ ACD ≌△ BCE(SAS), ∴ AD=BE.
(2)求∠ DOE 的度数;
解:∵△ ACD ≌△ BCE,
∴∠ ADC= ∠ BEC.
∵△ DCE 是等边三角形,
∴∠ CED= ∠ CDE=60°,
∴∠ ADE+ ∠ BED= ∠ ADC+ ∠ CDE+ ∠ BED
= ∠ ADC+60° + ∠ BED= ∠ CED+60°
=60° +60° =120°,
∴∠ DOE = 180° -(∠ ADE+ ∠ BED)=60° .
(3)求证:△ MNC 是等边三角形.
证明: 由(1) 可知∠ CAD= ∠ CBE,AD=BE,AC=BC.
又∵点M,N 分别是线段AD,BE 的中点,
∴ AM= AD,BN= BE,
∴ AM=BN.
在△ ACM 和△ BCN 中, AC=BC,
∠ CAM= ∠ CBN,
AM=BN,
∴△ ACM ≌△ BCN,
∴ CM=CN,∠ ACM= ∠ BCN.
又∵∠ ACB=60°,
∴∠ ACM+ ∠ MCB= ∠ BCN+ ∠ MCB=60° .
∴∠ MCN=60°,
∴△ MNC 是等边三角形.
(3)求证:△ MNC 是等边三角形.
又∵∠ ACB=60°,
∴∠ ACM+ ∠ MCB= ∠ BCN+ ∠ MCB=60° .
∴∠ MCN=60°,
∴△ MNC 是等边三角形.
定理 有两个角相等的三角形是等腰三角形.
简称“等角对等边”.
推论1 三个角都相等的三角形是等边三角形.
推论2 有一个角是60°的等腰三角形是等边三角形.
等腰三角形
的判定
等腰三角
形的判定
等边三角
形的判定
课堂小结
沪科版
15.3.3 等腰三角形的判定
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.领会等腰三角形、等边三角形的判定方法,培养合情推理的能力;
2.能够运用等腰三角形与等边三角形判定方法解答相关问题.
3.探索含30°角的直角三角形的性质.
学习目标
重点
难点
说出等腰三角形的性质
定理1 等腰三角形两个底角相等,简称“等边对等角”.
定理2 等腰三角形顶角的平分线垂直平分底边.
等腰三角形的两个底角相等,反过来的命题是否是真命题呢?请与你的同学研究讨论后作出判断.
一 等腰三角形的判定
新课引入
定理 有两个角相等的三角形是等腰三角形.简称“等角对等边”.
如何证明上面的定理呢?
已知:如图所示,在△ABC中,∠B=∠C.
求证:AB=AC.
新知学习
证明:过点A作AD⊥BC,D点为垂足,
∴∠ADB=∠ADC=90°.(垂直定义)
在△ADB和△ADC中,
∴△ADB≌△ADC.(AAS)
∴AB=AC(全等三角形的对应边相等)
这个定理叫做等腰三角形的判定定理,它是判断一个三角形是否为等腰三角形的重要依据.
通过该定理是否能得到其他推论?
注意:不能将等腰三角形的判定定理写成“如果一个三角形两个底角相等,那么它的两腰也相等”,因为在没有判断出三角形为等腰三角形前,不能使用“腰”、“底角”这类等腰三角形专用词语名称
推论1 三个角都相等的三角形是等边三角形.
推论2 有一个角是60°的等腰三角形是等边三角形.
你能对顶角是60°和底角是60°两种情况分类讨论吗?
二 等边三角形的判定
①顶角是60°
证:∵∠O=60°
∴∠A+∠B=120°.
∵△AOB是等腰三角形
∴∠A=∠B=∠O=60°
∴△AOB是等边三角形
②底角是60°
证:∵∠A=60°,且△AOB是等腰三角形
∴∠A=∠B=60°.
∴∠O=180°-∠A-∠B=60°
∴∠A=∠B=∠O=60°
∴△AOB是等边三角形
例1 已知:如图,AD∥BC,BD平分∠ABC.求证:AB=AD
B
A
D
C
证明:∵ AD∥BC,
∴∠ADB=∠DBC.
∵ BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD.
总结:角平分线+平行可得等腰三角形
例2 如图,一艘船从A处出发,以每时10n mile(海里)的速度向正北
航行,从A处测得一礁石C在北偏西30°的方向上.如果这艘船上午8:00从A处出发,10:00到达B处,从B处测得礁石C在北偏西60°的方向上.
(1)画出礁石C的位置;
(2)求从B处到礁石C的距离.
解:(1)以B为顶点,向北偏西60°作角,这角一边与AC交于点C,则点C为礁石所在地.
(2)∵∠ACB= 60°-30°=30°,(三角形的外角性质)
又∵∠BAC= 30°,∴∠BCA=∠BAC.
∴BC=BA.
∵BA=10×(10-8)=20(n mile)
∴BC=20(n mile).
即从 B处到礁石C的距离是20n mile.
1.如图,在△ABD中,C是BD上的一点,且AC⊥BD,AC=BC=CD.求证:
(1)△ABD是等腰三角形.
(2)求∠BAD的度数.
(1)证明:∵AC⊥BD,
∴∠ACB=∠ACD=90°,
又AC=BC=CD,
∴△ABC≌△ADC(SAS),
∴AB=AD,即△ABD是等腰三角形.
随堂练习
(2)由(1)可知,AB=AD,
∴∠B=∠D,又AC=BC=CD,
∴∠B=∠BAC,∠D=∠DAC.
在△ABD中,∠B+∠BAC+∠DAC+∠D=180°,
∴2(∠BAC+∠DAC)=180°,
∴∠BAC+∠DAC=90°,
∴∠BAD=∠BAC+∠DAC=90°.
2.如图,等边△ABC中,D、E、F分别是各边上的一点,且AD=BE=CF.
求证:△DEF是等边三角形.
证明:∵△ABC为等边三角形,且AD=BE=CF
∴AF=BD=CE,
又∵∠A=∠B=∠C=60°,
∴△ADF≌△BED≌△CFE(SAS),
∴DF=ED=FE,
∴△DEF是一个等边三角形.
3.如图,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于点F,试判断△AFC的形状,并说明理由.
解题思路:
1.证明△ABD≌△CBE(AAS)
2.全等三角形性质:对应边相等
(即为BA=BC)
3.等腰三角形性质:等边对等角
(即∠BAC=∠BCA)
4.再证明∠FAC=∠ACF.
4. 已知:如图15.3-13,△ ABC,△ CDE都是等边三角形,AD,BE 相交于点O,点M,N 分别是线段AD,BE 的中点.
(1)求证:AD=BE;
(2)求∠ DOE 的度数;
(3)求证:△ MNC 是等边三角形.
(1)求证:AD=BE;
证明:∵△ ABC,△ CDE 都是等边三角形,
∴ AC=BC,CD=CE,∠ ACB= ∠ DCE=60°,
∴∠ ACB+ ∠ BCD= ∠ DCE+ ∠ BCD,
∴∠ ACD= ∠ BCE.
在△ ACD 和△ BCE 中, AC=BC,
∠ ACD= ∠ BCE,
CD=CE,
∴△ ACD ≌△ BCE(SAS), ∴ AD=BE.
(2)求∠ DOE 的度数;
解:∵△ ACD ≌△ BCE,
∴∠ ADC= ∠ BEC.
∵△ DCE 是等边三角形,
∴∠ CED= ∠ CDE=60°,
∴∠ ADE+ ∠ BED= ∠ ADC+ ∠ CDE+ ∠ BED
= ∠ ADC+60° + ∠ BED= ∠ CED+60°
=60° +60° =120°,
∴∠ DOE = 180° -(∠ ADE+ ∠ BED)=60° .
(3)求证:△ MNC 是等边三角形.
证明: 由(1) 可知∠ CAD= ∠ CBE,AD=BE,AC=BC.
又∵点M,N 分别是线段AD,BE 的中点,
∴ AM= AD,BN= BE,
∴ AM=BN.
在△ ACM 和△ BCN 中, AC=BC,
∠ CAM= ∠ CBN,
AM=BN,
∴△ ACM ≌△ BCN,
∴ CM=CN,∠ ACM= ∠ BCN.
又∵∠ ACB=60°,
∴∠ ACM+ ∠ MCB= ∠ BCN+ ∠ MCB=60° .
∴∠ MCN=60°,
∴△ MNC 是等边三角形.
(3)求证:△ MNC 是等边三角形.
又∵∠ ACB=60°,
∴∠ ACM+ ∠ MCB= ∠ BCN+ ∠ MCB=60° .
∴∠ MCN=60°,
∴△ MNC 是等边三角形.
定理 有两个角相等的三角形是等腰三角形.
简称“等角对等边”.
推论1 三个角都相等的三角形是等边三角形.
推论2 有一个角是60°的等腰三角形是等边三角形.
等腰三角形
的判定
等腰三角
形的判定
等边三角
形的判定
课堂小结
