11.2实数第2课时实数的性质及大小比较课件(共26张PPT)2024-2025学年度八年级上册华师大版数学
文档属性
| 名称 | 11.2实数第2课时实数的性质及大小比较课件(共26张PPT)2024-2025学年度八年级上册华师大版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 363.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-09 12:09:16 | ||
图片预览






文档简介
(共26张PPT)
11.2.2 实数的性质及大小比较
八年级上
华师版
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.了解实数与数轴上点的一一对应关系.能用数轴上的点表示无理数.
2. 了解有理数的运算规律在实数范围内仍然适用.
学习目标
重点
难点
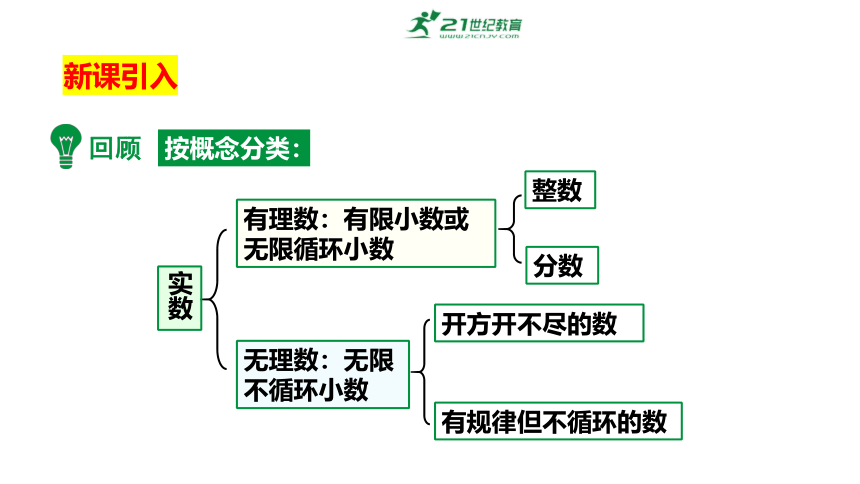
无理数:无限不循环小数
有理数:有限小数或无限循环小数
实数
分数
整数
开方开不尽的数
有规律但不循环的数
按概念分类:
回顾
新课引入
负实数
正实数
数实
正有理数
负有理数
按正负性分类:
0
正无理数
负无理数
0
正实数
负实数
一 实数与数轴上点的关系
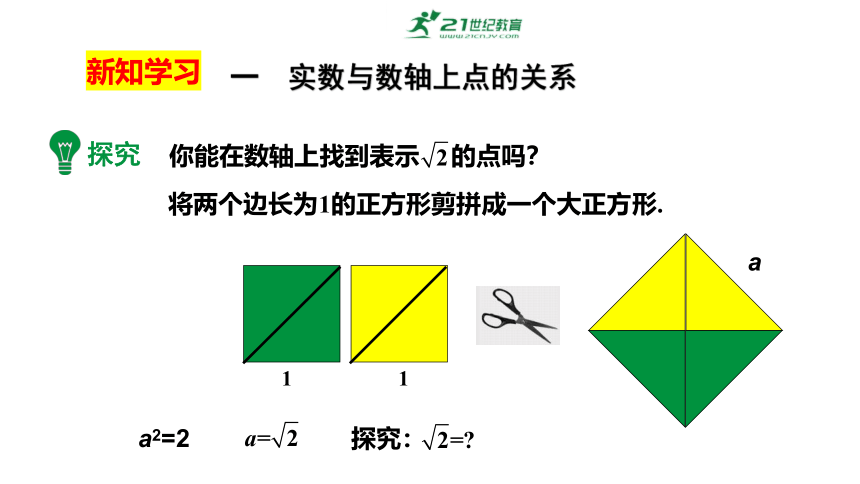
1
1
将两个边长为1的正方形剪拼成一个大正方形.
你能在数轴上找到表示 的点吗?
探究
a
a2=2
探究:
新知学习
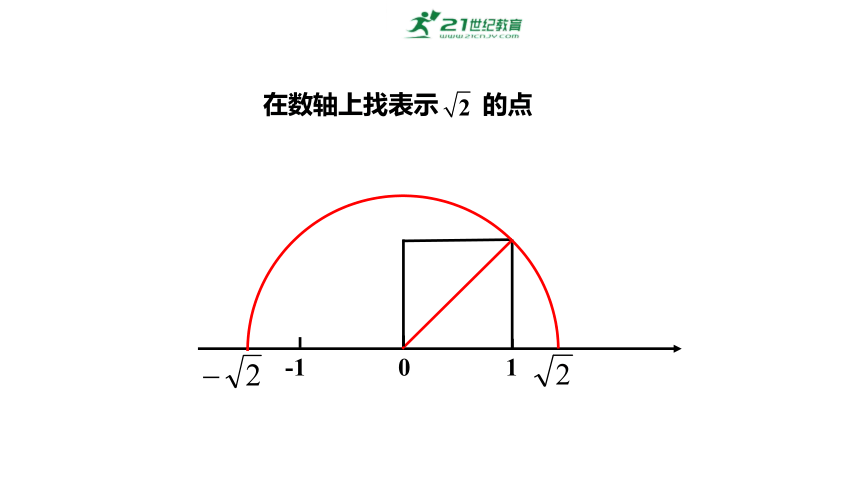
0
1
-1
在数轴上找表示 的点
归纳
数轴上的任一点必定表示一个实数;反过来,每一个实数(有理数或无理数)也都可以用数轴上的一个点来表示.
即:实数与数轴上的点一一对应.
例1 试比较 与π的大小关系.
解:用计算器求得
而
实数的大小比较和运算,通常可取它们的近似值来进行.
取近似值法
这样,容易判断
例2 试比较 与2的大小关系.
解: ,22 = 4
而 5 > 4
这样,容易判断
实数的大小比较和运算,通常可用乘方法来进行.
乘方法
实数的大小比较
1.借助数轴(左小右大);
2.借助绝对值 (两个负数比较,绝对值大的反而小);
3.借助计算器进行近似计算(适用于无理数);
4.乘方法;5.差值比较法;6.商值比较法;
7.倒数比较;8.规律法.
1.在 -3, ,-1, 0 这四个实数中,最大的是( )
A. -3 B.
C. -1 D. 0
D
针对训练
2.如图,在数轴上点A和点B之间的整数是 .
2
二 实数的性质
1. 相关概念
(1)相反数:实数a 的相反数为-a,若a、b 互为相反数,则a+b=0;
(2)倒数:非零实数a 的倒数为 ,若a、b 互为倒数,则ab=1;
(3)绝对值:|a|=
2. 法则法比较实数的大小
(1)定义法:正数大于0,0 大于一切负数.
(2)性质法:两个正数, 绝对值大的数大;两个负数,绝对值大的数反而小.
在有理数范围内的一些基本概念(如相反数、倒数、绝对值)在实数范围内依然适用.
温馨提示
解:(1) 相反数 - ,倒数 ,化为最简形式为 ,绝对值 .
(2) 相反数 2,倒数 ,绝对值 2.
(3) 相反数 -7,倒数 ,绝对值 7.
例3. 求下列各数的相反数、倒数和绝对值:
(1) (2) (3)
三 实数的运算
1. 实数混合运算的运算顺序与有理数混合运算的运算顺序一样,即先算乘方、开方,再算乘除,最后算加减,同级运算按照自左向右的顺序进行,有括号的先算括号里面的.
2. 实数的运算律
加法交换律:a + b = b + a;
加法结合律:(a + b) + c = a + (b + c);
乘法交换律:ab = ba;
乘法结合律:(ab)c = a(bc);
乘法分配律:(a + b)c = ac + bc.
3. 运算种类
运算 级别 第一级 第二级 第三级 运算 名称 加 减 乘 除 乘方 开方
运算 结果 和 差 积 商 幂 方根
有理数的运算律在实数范围内仍然适用,在进行实数运算的过程中,要做到:
一“ 看” ——看算式的结构特点,能否运用运算律或公式;二“ 用” ——运用运算律或公式;
三“ 查” ——检查过程和结果是否正确.
温馨提示
例4 计算: . (结果精确到0.01)
解: 用计算器求得
于是
所以
1.计算:(结果精确到0.01)
解:原式=
=
≈
1.414+0.333+6.284
=
8.031
≈
8.03
随堂练习
2 比较 与2.6的大小.
解:∵9<12<16,
∴3< <4,
∴2< <2.5,
∴ <2.6.
2. 如图,实数a,b,c在数轴上的位置如图所示,化简:|a-b|+
- .
解:由数轴上a,b,c三点的相对位置可知,a<0,b<0,c>0,b∴a-b>0,a-c<0,a+b<0,
∴|a-b|+ - =a-b+(c-a)-(a+b)=a-b+c-a-a-b
=-a-2b+c,
∴原式=-a-2b+c.
实数的性质
及大小比较
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.
有理数和无理数统称实数
实数与数轴上点的一一对应
课堂小结
1. 实数混合运算的运算顺序与有理数混合运算的运算顺序一样,即先算乘方、开方,再算乘除,最后算加减,同级运算按照自左向右的顺序进行,有括号的先算括号里面的.
运算 级别 第一级 第二级 第三级 运算 名称 加 减 乘 除 乘方 开方
运算 结果 和 差 积 商 幂 方根
11.2.2 实数的性质及大小比较
八年级上
华师版
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.了解实数与数轴上点的一一对应关系.能用数轴上的点表示无理数.
2. 了解有理数的运算规律在实数范围内仍然适用.
学习目标
重点
难点
无理数:无限不循环小数
有理数:有限小数或无限循环小数
实数
分数
整数
开方开不尽的数
有规律但不循环的数
按概念分类:
回顾
新课引入
负实数
正实数
数实
正有理数
负有理数
按正负性分类:
0
正无理数
负无理数
0
正实数
负实数
一 实数与数轴上点的关系
1
1
将两个边长为1的正方形剪拼成一个大正方形.
你能在数轴上找到表示 的点吗?
探究
a
a2=2
探究:
新知学习
0
1
-1
在数轴上找表示 的点
归纳
数轴上的任一点必定表示一个实数;反过来,每一个实数(有理数或无理数)也都可以用数轴上的一个点来表示.
即:实数与数轴上的点一一对应.
例1 试比较 与π的大小关系.
解:用计算器求得
而
实数的大小比较和运算,通常可取它们的近似值来进行.
取近似值法
这样,容易判断
例2 试比较 与2的大小关系.
解: ,22 = 4
而 5 > 4
这样,容易判断
实数的大小比较和运算,通常可用乘方法来进行.
乘方法
实数的大小比较
1.借助数轴(左小右大);
2.借助绝对值 (两个负数比较,绝对值大的反而小);
3.借助计算器进行近似计算(适用于无理数);
4.乘方法;5.差值比较法;6.商值比较法;
7.倒数比较;8.规律法.
1.在 -3, ,-1, 0 这四个实数中,最大的是( )
A. -3 B.
C. -1 D. 0
D
针对训练
2.如图,在数轴上点A和点B之间的整数是 .
2
二 实数的性质
1. 相关概念
(1)相反数:实数a 的相反数为-a,若a、b 互为相反数,则a+b=0;
(2)倒数:非零实数a 的倒数为 ,若a、b 互为倒数,则ab=1;
(3)绝对值:|a|=
2. 法则法比较实数的大小
(1)定义法:正数大于0,0 大于一切负数.
(2)性质法:两个正数, 绝对值大的数大;两个负数,绝对值大的数反而小.
在有理数范围内的一些基本概念(如相反数、倒数、绝对值)在实数范围内依然适用.
温馨提示
解:(1) 相反数 - ,倒数 ,化为最简形式为 ,绝对值 .
(2) 相反数 2,倒数 ,绝对值 2.
(3) 相反数 -7,倒数 ,绝对值 7.
例3. 求下列各数的相反数、倒数和绝对值:
(1) (2) (3)
三 实数的运算
1. 实数混合运算的运算顺序与有理数混合运算的运算顺序一样,即先算乘方、开方,再算乘除,最后算加减,同级运算按照自左向右的顺序进行,有括号的先算括号里面的.
2. 实数的运算律
加法交换律:a + b = b + a;
加法结合律:(a + b) + c = a + (b + c);
乘法交换律:ab = ba;
乘法结合律:(ab)c = a(bc);
乘法分配律:(a + b)c = ac + bc.
3. 运算种类
运算 级别 第一级 第二级 第三级 运算 名称 加 减 乘 除 乘方 开方
运算 结果 和 差 积 商 幂 方根
有理数的运算律在实数范围内仍然适用,在进行实数运算的过程中,要做到:
一“ 看” ——看算式的结构特点,能否运用运算律或公式;二“ 用” ——运用运算律或公式;
三“ 查” ——检查过程和结果是否正确.
温馨提示
例4 计算: . (结果精确到0.01)
解: 用计算器求得
于是
所以
1.计算:(结果精确到0.01)
解:原式=
=
≈
1.414+0.333+6.284
=
8.031
≈
8.03
随堂练习
2 比较 与2.6的大小.
解:∵9<12<16,
∴3< <4,
∴2< <2.5,
∴ <2.6.
2. 如图,实数a,b,c在数轴上的位置如图所示,化简:|a-b|+
- .
解:由数轴上a,b,c三点的相对位置可知,a<0,b<0,c>0,b
∴|a-b|+ - =a-b+(c-a)-(a+b)=a-b+c-a-a-b
=-a-2b+c,
∴原式=-a-2b+c.
实数的性质
及大小比较
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.
有理数和无理数统称实数
实数与数轴上点的一一对应
课堂小结
1. 实数混合运算的运算顺序与有理数混合运算的运算顺序一样,即先算乘方、开方,再算乘除,最后算加减,同级运算按照自左向右的顺序进行,有括号的先算括号里面的.
运算 级别 第一级 第二级 第三级 运算 名称 加 减 乘 除 乘方 开方
运算 结果 和 差 积 商 幂 方根
