人教版2019高中物理必修一2.4自由落体运动(共29张PPT)
文档属性
| 名称 | 人教版2019高中物理必修一2.4自由落体运动(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-06 10:33:49 | ||
图片预览







文档简介
(共29张PPT)
第二章 匀变速直线运动的研究
专题 竖直上抛运动
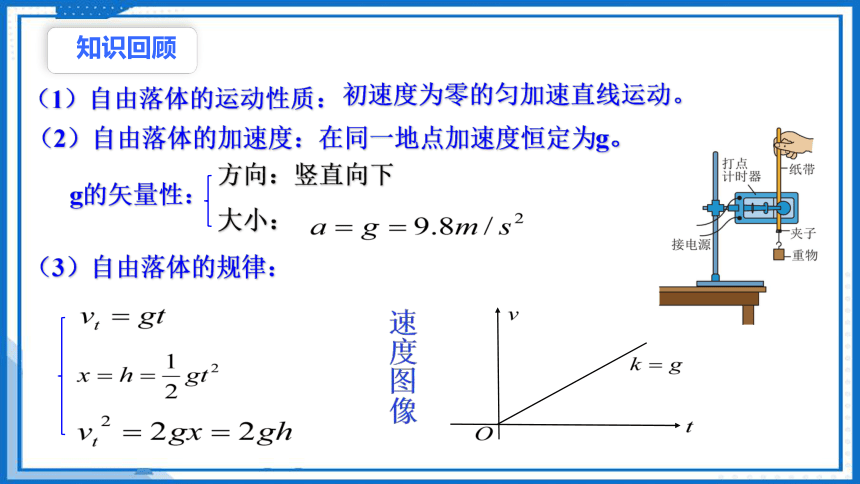
(1)自由落体的运动性质:
方向:竖直向下
(2)自由落体的加速度:在同一地点加速度恒定为g。
g的矢量性:
大小:
(3)自由落体的规律:
知识回顾
初速度为零的匀加速直线运动。
如果忽略空气阻力,我们可以把运动员从最高点竖直下落的过程看成自由落体运动。那么,运动员竖直向上的过程又是什么样的运动呢?
想一想
竖直上抛运动
01
1.定义:将物体以一定的初速度竖直向上抛出,物体只在重力作用下的运动叫做竖直上抛运动。
2.产生条件:①具有竖直向上的初速度;
②只受重力作用。
3.运动的性质:
初速度v0 >0,加速度a=-g的匀减速直线运动。(一般规定:竖直向上为正方向)
a → -g
x → h
竖直上抛运动是加速度大小为g的匀变速直线运动,所以,匀变速直线运动公式同样也适用于竖直上抛运动。
v0=0
4、竖直上抛运动的规律:
(1)上升到最高点的时间:
(2)上升到最大高度:
(3)上升与下降对称:
时间对称性:
速度对称性:
A
A
VA
VA
①物体上升到最高点所用时间与物体从最高点落回到原抛出点所用时间相等,即t上= t下
②从抛出点到某点A与从某点A到抛出点时间相同。
①上抛时的初速度与落回原抛出点的速度大小相等、方向相反。
②上升与下降阶段经过同一位置A时的速度大小相等,方向相反。
最高点:v=0,a=g
5、竖直上抛运动的特点:
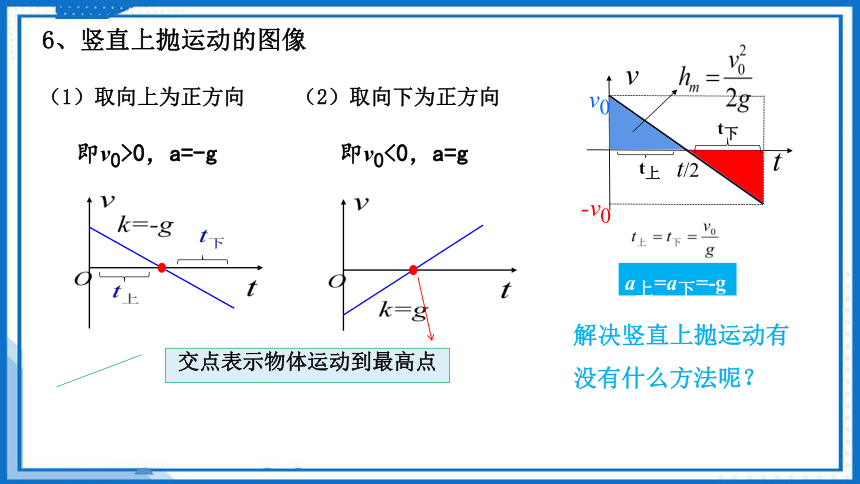
(1)取向上为正方向
即v0>0,a=-g
交点表示物体运动到最高点
(2)取向下为正方向
即v0<0,a=g
6、竖直上抛运动的图像
t
v
v0
-v0
解决竖直上抛运动有没有什么方法呢?
t/2
t上
t下
a上=a下=-g
整个竖直上抛运动可分为上升和下降两个阶段,但其本质是初速度为 v0 加速度a= - g的匀变速直线运动,处理时常采用以下两种方法:
(1)分段法:
(2)整体法:对全程列式,通常取竖直向上为正
①落地点在抛出点上方(正位移)
②落地点在抛出点下方(负位移)
上升阶段:末速度为零的匀减速直线运动
下降阶段:自由落体运动
v0
v = 0
vt
vt
v0
7、竖直上抛运动的处理方法
【例题】气球下挂一重物,以v0=10m/s匀速上升,当到达离地高h=175m处时,悬挂重物的绳子突然断裂(空气阻力不计,取g=10m/s2),求:
(1)重物经多少时间落到地面?
(2)重物落地的速度多大?
【答案】 (1)t=7s(2)60m/s
类竖直上抛问题
02
如图,沿粗糙斜面上滑的小球,到最高点后仍能下滑,上下过程加速度大小不同但位移大小相同,若上滑时的加速度为a1,下滑时的加速度为a2,求解时可拆解为两个初速度为0的匀加速直线运动进行简化。
特点:初(或末)速度为零,两段运动位移大小相等为x。
位移三个公式:
等位移折返模型
如图,物体从A点由静止出发做匀加速直线运动,加速度大小为a1,运动到B点时速度大小为v1,这时立即以大小为a2的加速度做匀减速直线运动,如果经过相等的时间物体回到了原出发点。
物体速度应先减速到0再返回出发点A,速度为v2,从A点运动到B点的时间等于由B回到A点的时间,设为t,取向右为正方向,
从B返回A:
物体从A到B:
等时间折返模型
典例分析
03
【例题】关于竖直上抛运动,下列说法正确的是( )
A.上升过程和下落过程加速度大小相等,方向相同
B.上升过程和下落过程加速度大小相等,方向相反
C.在最高点物体速度为零,加速度不为零
D.在最高点物体速度为零,加速度为零
A C
【例题】(多选)某校一课外活动小组自制了一枚火箭,设火箭发射后始终在垂直于地面的方向上运动。火箭点火后可认为做匀加速直线运动,经过6s到达离地面60m处燃料恰好用完,下列说法正确的是(不计空气阻力,g取10m/s2)( )
A.火箭上升离地面的最大高度为80m
B.燃料恰好用完后火箭还能继续上升的时间为3s
C.火箭从发射到返回发射点的时间为12s
D.火箭落地速度为30m/s
AC
【例题】(多选)甲乙两小球先后以同样的速度在距地面不同高度处竖直向上抛出,抛出时间相隔2s,它们运动的图像分别如直线甲乙所示。则( )
A.t = 4s时,两球相对于各自的抛出点的位移相等
B.t = 2s时,两球的高度相差一定为40m
C.甲球从抛出至到达最高点的时间间隔与乙球相等
D.两球从抛出至落到地面所用的时间间隔相等
AC
【例题】位于瑞士的世界上最大的人工喷泉——日内瓦喷泉如图所示.已知该喷泉竖直向上喷出,喷出时水的速度为53m/s,喷嘴的出水量为0.5m3/s,不计空气阻力,则空中水的体积应为(g取10m/s2)( )
A.2.65m3 B.5.3m3
C.10.6m3 D.15.9m3
B
【例题】(多选)如图所示,长度为0.65m的圆筒竖直放在水平地面上,在圆筒正上方距其上端1.80m处有一小球(可视为质点,能无摩擦地穿过圆筒)。在由静止释放小球的同时,将圆筒竖直向上抛出,在圆筒落地前的瞬间,小球在圆筒内运动而没有落地,则圆筒上抛的速度大小可能为(空气阻力不计,g取10m/s2)( )
A.3.1m/s B.3.3m/s
C.3.5m/s D.3.7m/s
ABC
【例题】一个物体从高度h处自由下落,测得物体落地前最后1秒内下落了25米,求:物体下落的高度h. (g取10m/s2)
解一:画出运动示意图,设落地总时间为t, 则依题意,
h
25m
1s
(t-1)s
t
O
A
B
由自由落体运动规律得
O到B h=1/2×gt2 (1)
O到A h-25 = 1/2× g(t-1)2 (2)
解得 t=3s, h=45m
解二:A→B 由位移公式有
hAB = vA× 1 +1/2× g×12 = 25
∴ vA= 20m/s
O到A 由自由落体运动规律得
h-25 = vA2 / 2g=20m
∴h=45m
h
25m
1s
(t-1)s
t
O
A
B
解三:O →A 自由落体运动 vA =g(t –1)
O →B 自由落体运动 vB =gt
A →B 竖直下抛运动 vB2- vA2 =2g×25
g 2 t 2- g 2 (t –1)2 =2g×25
解出 t=3s, h=45m
解四: A →B 平均速度为
(vA+vB)/ 2 =25
A →B 由速度公式有: vB =vA+g×1
∴vB =30m/s
O →B 自由落体运动
∴ h= vB2/2g=45 m
h
25m
1s
(t-1)s
t
O
A
B
解五: 自由落体运动第一秒下落的位移为
hⅠ=1/2g × 1= 5m
由自由落体运动的比例关系
hⅠ﹕hⅡ﹕h Ⅲ﹕… = 1 ﹕ 3﹕ 5﹕ …
=5 ﹕ 15﹕ 25﹕ …
∴ t=3s h=5+15+25=45m
解六: 由自由落体运动的速度图线 ,
0
t/s
v/ms-1
t -1
t
d
a
b
c
梯形面积等于最后1s内的位移,
ab=g(t-1) cd=gt bc= 1s
25=1/2 ×[gt+g(t-1)] ×1
∴ t=3s h=1/2×gt2=45m
答案 (1)1 m/s (2)会
【例题】球A从高为2 m的位置自由下落,同时球A正下方的球B由地面以5 m/s的速度向上抛出,求:(g取10 m/s2,不计空气阻力)
(1)两球相遇时B球的速度大小;
(2)若B球以4 m/s的速度抛出,两球会不会在空中相遇
假设两球会在空中相遇,设相遇时间为t′
B球在空中运动的时间为tB
由于t′解:设两球相遇所需时间为t
vB=v0-gt得vB=1 m/s
公式+规律
竖直上抛
将物体以一定的初速度竖直向上抛出,物体只在重力作用下的运动叫做竖直上抛运动。
v0
v = 0
vt
vt
v0
运动的性质:初速度v0 >0,加速度a=-g的匀减速直线运动。
处理方法
t
v
v0
-v0
t/2
分段法
+
整体法
课堂小结
分段研究
上升
下降
全程研究
对称性
时间对称
速度对称
t
v
v0
-v0
v0
v = 0
vt
vt
v0
设向上为正
设向下为正
设向上为正
t/2
注意各矢量(s,v,g)的方向
课后小结
第二章 匀变速直线运动的研究
专题 竖直上抛运动
(1)自由落体的运动性质:
方向:竖直向下
(2)自由落体的加速度:在同一地点加速度恒定为g。
g的矢量性:
大小:
(3)自由落体的规律:
知识回顾
初速度为零的匀加速直线运动。
如果忽略空气阻力,我们可以把运动员从最高点竖直下落的过程看成自由落体运动。那么,运动员竖直向上的过程又是什么样的运动呢?
想一想
竖直上抛运动
01
1.定义:将物体以一定的初速度竖直向上抛出,物体只在重力作用下的运动叫做竖直上抛运动。
2.产生条件:①具有竖直向上的初速度;
②只受重力作用。
3.运动的性质:
初速度v0 >0,加速度a=-g的匀减速直线运动。(一般规定:竖直向上为正方向)
a → -g
x → h
竖直上抛运动是加速度大小为g的匀变速直线运动,所以,匀变速直线运动公式同样也适用于竖直上抛运动。
v0=0
4、竖直上抛运动的规律:
(1)上升到最高点的时间:
(2)上升到最大高度:
(3)上升与下降对称:
时间对称性:
速度对称性:
A
A
VA
VA
①物体上升到最高点所用时间与物体从最高点落回到原抛出点所用时间相等,即t上= t下
②从抛出点到某点A与从某点A到抛出点时间相同。
①上抛时的初速度与落回原抛出点的速度大小相等、方向相反。
②上升与下降阶段经过同一位置A时的速度大小相等,方向相反。
最高点:v=0,a=g
5、竖直上抛运动的特点:
(1)取向上为正方向
即v0>0,a=-g
交点表示物体运动到最高点
(2)取向下为正方向
即v0<0,a=g
6、竖直上抛运动的图像
t
v
v0
-v0
解决竖直上抛运动有没有什么方法呢?
t/2
t上
t下
a上=a下=-g
整个竖直上抛运动可分为上升和下降两个阶段,但其本质是初速度为 v0 加速度a= - g的匀变速直线运动,处理时常采用以下两种方法:
(1)分段法:
(2)整体法:对全程列式,通常取竖直向上为正
①落地点在抛出点上方(正位移)
②落地点在抛出点下方(负位移)
上升阶段:末速度为零的匀减速直线运动
下降阶段:自由落体运动
v0
v = 0
vt
vt
v0
7、竖直上抛运动的处理方法
【例题】气球下挂一重物,以v0=10m/s匀速上升,当到达离地高h=175m处时,悬挂重物的绳子突然断裂(空气阻力不计,取g=10m/s2),求:
(1)重物经多少时间落到地面?
(2)重物落地的速度多大?
【答案】 (1)t=7s(2)60m/s
类竖直上抛问题
02
如图,沿粗糙斜面上滑的小球,到最高点后仍能下滑,上下过程加速度大小不同但位移大小相同,若上滑时的加速度为a1,下滑时的加速度为a2,求解时可拆解为两个初速度为0的匀加速直线运动进行简化。
特点:初(或末)速度为零,两段运动位移大小相等为x。
位移三个公式:
等位移折返模型
如图,物体从A点由静止出发做匀加速直线运动,加速度大小为a1,运动到B点时速度大小为v1,这时立即以大小为a2的加速度做匀减速直线运动,如果经过相等的时间物体回到了原出发点。
物体速度应先减速到0再返回出发点A,速度为v2,从A点运动到B点的时间等于由B回到A点的时间,设为t,取向右为正方向,
从B返回A:
物体从A到B:
等时间折返模型
典例分析
03
【例题】关于竖直上抛运动,下列说法正确的是( )
A.上升过程和下落过程加速度大小相等,方向相同
B.上升过程和下落过程加速度大小相等,方向相反
C.在最高点物体速度为零,加速度不为零
D.在最高点物体速度为零,加速度为零
A C
【例题】(多选)某校一课外活动小组自制了一枚火箭,设火箭发射后始终在垂直于地面的方向上运动。火箭点火后可认为做匀加速直线运动,经过6s到达离地面60m处燃料恰好用完,下列说法正确的是(不计空气阻力,g取10m/s2)( )
A.火箭上升离地面的最大高度为80m
B.燃料恰好用完后火箭还能继续上升的时间为3s
C.火箭从发射到返回发射点的时间为12s
D.火箭落地速度为30m/s
AC
【例题】(多选)甲乙两小球先后以同样的速度在距地面不同高度处竖直向上抛出,抛出时间相隔2s,它们运动的图像分别如直线甲乙所示。则( )
A.t = 4s时,两球相对于各自的抛出点的位移相等
B.t = 2s时,两球的高度相差一定为40m
C.甲球从抛出至到达最高点的时间间隔与乙球相等
D.两球从抛出至落到地面所用的时间间隔相等
AC
【例题】位于瑞士的世界上最大的人工喷泉——日内瓦喷泉如图所示.已知该喷泉竖直向上喷出,喷出时水的速度为53m/s,喷嘴的出水量为0.5m3/s,不计空气阻力,则空中水的体积应为(g取10m/s2)( )
A.2.65m3 B.5.3m3
C.10.6m3 D.15.9m3
B
【例题】(多选)如图所示,长度为0.65m的圆筒竖直放在水平地面上,在圆筒正上方距其上端1.80m处有一小球(可视为质点,能无摩擦地穿过圆筒)。在由静止释放小球的同时,将圆筒竖直向上抛出,在圆筒落地前的瞬间,小球在圆筒内运动而没有落地,则圆筒上抛的速度大小可能为(空气阻力不计,g取10m/s2)( )
A.3.1m/s B.3.3m/s
C.3.5m/s D.3.7m/s
ABC
【例题】一个物体从高度h处自由下落,测得物体落地前最后1秒内下落了25米,求:物体下落的高度h. (g取10m/s2)
解一:画出运动示意图,设落地总时间为t, 则依题意,
h
25m
1s
(t-1)s
t
O
A
B
由自由落体运动规律得
O到B h=1/2×gt2 (1)
O到A h-25 = 1/2× g(t-1)2 (2)
解得 t=3s, h=45m
解二:A→B 由位移公式有
hAB = vA× 1 +1/2× g×12 = 25
∴ vA= 20m/s
O到A 由自由落体运动规律得
h-25 = vA2 / 2g=20m
∴h=45m
h
25m
1s
(t-1)s
t
O
A
B
解三:O →A 自由落体运动 vA =g(t –1)
O →B 自由落体运动 vB =gt
A →B 竖直下抛运动 vB2- vA2 =2g×25
g 2 t 2- g 2 (t –1)2 =2g×25
解出 t=3s, h=45m
解四: A →B 平均速度为
(vA+vB)/ 2 =25
A →B 由速度公式有: vB =vA+g×1
∴vB =30m/s
O →B 自由落体运动
∴ h= vB2/2g=45 m
h
25m
1s
(t-1)s
t
O
A
B
解五: 自由落体运动第一秒下落的位移为
hⅠ=1/2g × 1= 5m
由自由落体运动的比例关系
hⅠ﹕hⅡ﹕h Ⅲ﹕… = 1 ﹕ 3﹕ 5﹕ …
=5 ﹕ 15﹕ 25﹕ …
∴ t=3s h=5+15+25=45m
解六: 由自由落体运动的速度图线 ,
0
t/s
v/ms-1
t -1
t
d
a
b
c
梯形面积等于最后1s内的位移,
ab=g(t-1) cd=gt bc= 1s
25=1/2 ×[gt+g(t-1)] ×1
∴ t=3s h=1/2×gt2=45m
答案 (1)1 m/s (2)会
【例题】球A从高为2 m的位置自由下落,同时球A正下方的球B由地面以5 m/s的速度向上抛出,求:(g取10 m/s2,不计空气阻力)
(1)两球相遇时B球的速度大小;
(2)若B球以4 m/s的速度抛出,两球会不会在空中相遇
假设两球会在空中相遇,设相遇时间为t′
B球在空中运动的时间为tB
由于t′
vB=v0-gt得vB=1 m/s
公式+规律
竖直上抛
将物体以一定的初速度竖直向上抛出,物体只在重力作用下的运动叫做竖直上抛运动。
v0
v = 0
vt
vt
v0
运动的性质:初速度v0 >0,加速度a=-g的匀减速直线运动。
处理方法
t
v
v0
-v0
t/2
分段法
+
整体法
课堂小结
分段研究
上升
下降
全程研究
对称性
时间对称
速度对称
t
v
v0
-v0
v0
v = 0
vt
vt
v0
设向上为正
设向下为正
设向上为正
t/2
注意各矢量(s,v,g)的方向
课后小结
