九年级上册数学北师大版 第五周 周测数学试卷(含详解)
文档属性
| 名称 | 九年级上册数学北师大版 第五周 周测数学试卷(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 330.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-06 10:45:29 | ||
图片预览



文档简介
第五周—九年级上册数学北师大版(2012)每周测验
考查范围:2.4-2.6
1.方程的根的符号是( )
A.两根一正一负 B.两根都是负数 C.两根都是正数 D.无法确定
2.为迎接端午促销活动,某服装店从6月份开始对春装进行“折上折“(两次打折数相同)优惠活动,已知一件原价500元的春装,优惠后实际仅需320元,设该店春装原本打x折,则有( )
A. B.
C. D.
3.若是关于x的一元二次方程的一个根,则此方程的另一个根是( )
A.6 B.4 C.3 D.
4.世界卫生组织关于埃博拉疫情报告称,在病毒传播中,每轮平均1人会感染x个人,若2个人患病,则经过两轮感染就共有162人患病.求x的值( )
A.9 B.8 C.7 D.6
5.已知、是关于x的一元二次方程的两个不相等的实数根,且满足,则m的值是( )
A.3 B.1 C.3或 D.或1
6.已知关于y的一元二次方程的根都是整数,且m满足等式,则满足条件的所有整数m的和是( )
A.-5 B.-4 C.0 D.-6
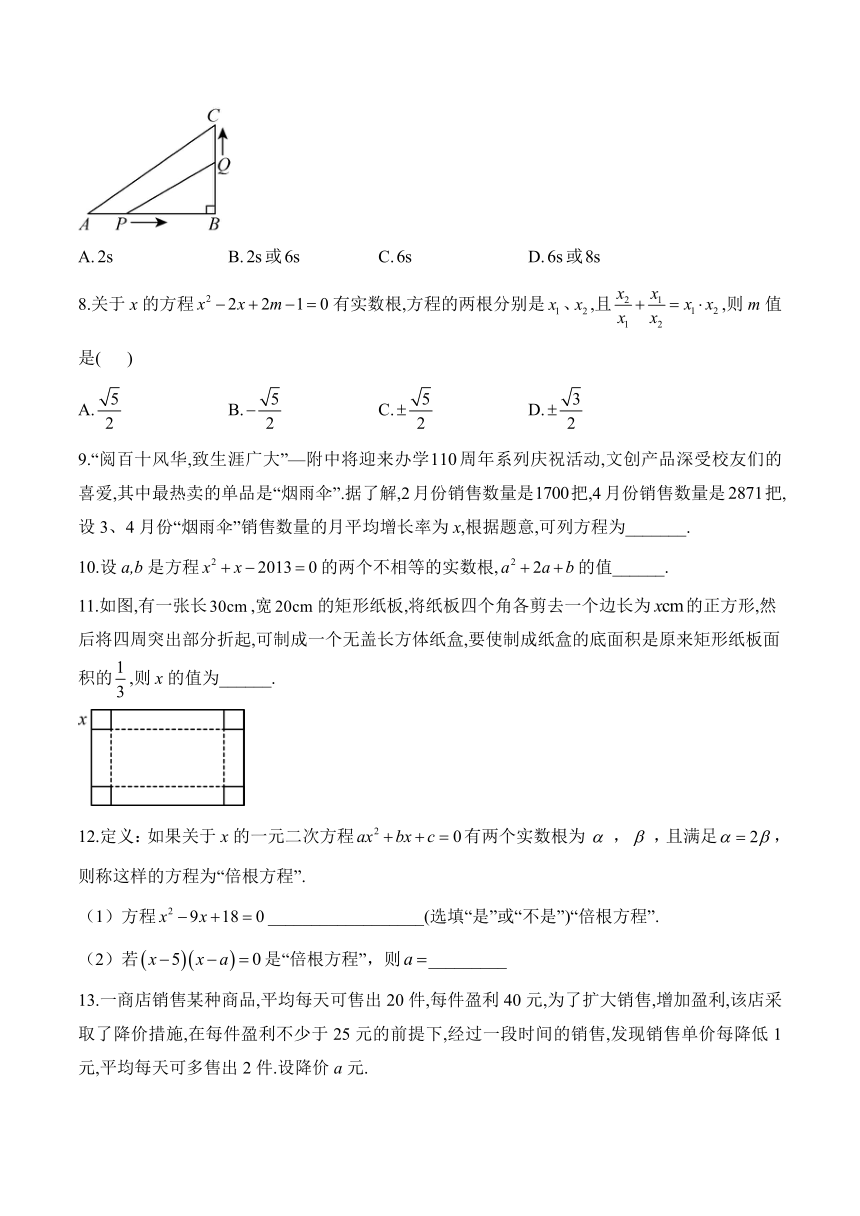
7.如图,在中,,,,点P沿边从点A出发向终点B以的速度移动;同时点Q沿边从点B出发向终点C以的速度移动,当其中一点到达终点时,另一点也随之停止移动.当的面积为时,点P运动的时间是( )
A. B.或 C. D.或
8.关于x的方程有实数根,方程的两根分别是、,且,则m值是( )
A. B. C. D.
9.“阅百十风华,致生涯广大”—附中将迎来办学周年系列庆祝活动,文创产品深受校友们的喜爱,其中最热卖的单品是“烟雨伞”.据了解,2月份销售数量是把,4月份销售数量是把,设3、4月份“烟雨伞”销售数量的月平均增长率为x,根据题意,可列方程为_______.
10.设a,b是方程的两个不相等的实数根,的值______.
11.如图,有一张长,宽的矩形纸板,将纸板四个角各剪去一个边长为的正方形,然后将四周突出部分折起,可制成一个无盖长方体纸盒,要使制成纸盒的底面积是原来矩形纸板面积的,则x的值为______.
12.定义:如果关于x的一元二次方程有两个实数根为,,且满足,则称这样的方程为“倍根方程”.
(1)方程__________________(选填“是”或“不是”)“倍根方程”.
(2)若是“倍根方程”,则_________
13.一商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间的销售,发现销售单价每降低1元,平均每天可多售出2件.设降价a元.
(1)平均每天的销售数量为___________件(用含a的式子表示),
(2)该商店每天的销售利润能达到1200元吗?若能达到,请求出a的值:若不能达到,请说明理由.
14.实数k使关于x的方程有两个实数根,.
(1)求k的取值范围;
(2)若,求k的值;
答案以及解析
1.答案:C
解析:,
,
解得,,
方程的两根都是正数.故选C.
2.答案:C
解析:设该店春装原本打x折,
依题意,得:.
故选C.
3.答案:C
解析:∵关于x的一元二次方程的一个根是2,
∴把代入原方程,得,
,
∴原方程为,即,
或,
解得或,
故选:C.
4.答案:B
解析:若2个人患病,则第一轮传染中感染2x人,第二轮传染中感染x(2+2x)人,
依题意得:,
即,
解得:,(不符合题意,舍去),
∴x的值为8.
故选:B.
5.答案:A
解析:∵、是关于x的一元二次方程的两个不相等的实数根,
∴,
解得:,
又∵,,,
∴,
∴
即
解得:或,
∵,
∴,
故选:A.
6.答案:D
解析:满足等式,
,解得,
,
,
解得,,
关于y的一元二次方程的根都是整数,且,m是整数,
或-2或-4,
满足条件的所有整数m的和是.
故选D.
7.答案:A
解析:设运动时间为t,
∵在中,,,,点P沿边从点A出发向终点B以的速度移动;同时点Q沿边从点B出发向终点C以的速度移动,
∴,,
∵的面积为,
∴,
解得:,,
∵点P在上的运动时间为:,
∴,
∴不符合题意,
∴点P的运动时间为,的面积为,故A正确,符合题意.
故选:A.
8.答案:B
解析:关于的方程有实数根,方程的两根分别是、,
,,
,
,
,
,
整理得:,
解得,
,
,
故选:B.
9.答案:
解析:依题意得,,
故答案为:.
10.答案:2012
解析:根据韦达定理可得:,,
∴原式.
故答案为:2012.
11.答案:5
解析:由题意可知,无盖纸盒的长为,宽为,
∴,
整理得,
解得,(不合题意,舍去),
故x的值为5.
故答案为:5.
12.答案:①是
②或
解析:(1),
,
解得,
,
方程是“倍根方程”.
故答案为:是;
(2)解方程得,
是“倍根方程”,
或,
故答案为:或.
13.答案:(1)
(2)能,
解析:(1)(件).
故答案为:;
(2)设每件衬衫降价x元,则每件盈利元,每天可以售出件,
依题意得:,
整理得:,
解得:,.
又∵每件盈利不少于25元,即,
,
.
答:当每件商品降价10元时,即,该商店每天销售利润为1200元.
14.答案:(1)k的取值范围为
(2)k的值为0或
解析:(1)方程化为一般式为,
根据题意得,解得,
即k的取值范围为;
(2)根据根与系数的关系得,,
∵,
∴,
∴,
∴,整理得,
解得,,
∵,
∴k的值为0或.
考查范围:2.4-2.6
1.方程的根的符号是( )
A.两根一正一负 B.两根都是负数 C.两根都是正数 D.无法确定
2.为迎接端午促销活动,某服装店从6月份开始对春装进行“折上折“(两次打折数相同)优惠活动,已知一件原价500元的春装,优惠后实际仅需320元,设该店春装原本打x折,则有( )
A. B.
C. D.
3.若是关于x的一元二次方程的一个根,则此方程的另一个根是( )
A.6 B.4 C.3 D.
4.世界卫生组织关于埃博拉疫情报告称,在病毒传播中,每轮平均1人会感染x个人,若2个人患病,则经过两轮感染就共有162人患病.求x的值( )
A.9 B.8 C.7 D.6
5.已知、是关于x的一元二次方程的两个不相等的实数根,且满足,则m的值是( )
A.3 B.1 C.3或 D.或1
6.已知关于y的一元二次方程的根都是整数,且m满足等式,则满足条件的所有整数m的和是( )
A.-5 B.-4 C.0 D.-6
7.如图,在中,,,,点P沿边从点A出发向终点B以的速度移动;同时点Q沿边从点B出发向终点C以的速度移动,当其中一点到达终点时,另一点也随之停止移动.当的面积为时,点P运动的时间是( )
A. B.或 C. D.或
8.关于x的方程有实数根,方程的两根分别是、,且,则m值是( )
A. B. C. D.
9.“阅百十风华,致生涯广大”—附中将迎来办学周年系列庆祝活动,文创产品深受校友们的喜爱,其中最热卖的单品是“烟雨伞”.据了解,2月份销售数量是把,4月份销售数量是把,设3、4月份“烟雨伞”销售数量的月平均增长率为x,根据题意,可列方程为_______.
10.设a,b是方程的两个不相等的实数根,的值______.
11.如图,有一张长,宽的矩形纸板,将纸板四个角各剪去一个边长为的正方形,然后将四周突出部分折起,可制成一个无盖长方体纸盒,要使制成纸盒的底面积是原来矩形纸板面积的,则x的值为______.
12.定义:如果关于x的一元二次方程有两个实数根为,,且满足,则称这样的方程为“倍根方程”.
(1)方程__________________(选填“是”或“不是”)“倍根方程”.
(2)若是“倍根方程”,则_________
13.一商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间的销售,发现销售单价每降低1元,平均每天可多售出2件.设降价a元.
(1)平均每天的销售数量为___________件(用含a的式子表示),
(2)该商店每天的销售利润能达到1200元吗?若能达到,请求出a的值:若不能达到,请说明理由.
14.实数k使关于x的方程有两个实数根,.
(1)求k的取值范围;
(2)若,求k的值;
答案以及解析
1.答案:C
解析:,
,
解得,,
方程的两根都是正数.故选C.
2.答案:C
解析:设该店春装原本打x折,
依题意,得:.
故选C.
3.答案:C
解析:∵关于x的一元二次方程的一个根是2,
∴把代入原方程,得,
,
∴原方程为,即,
或,
解得或,
故选:C.
4.答案:B
解析:若2个人患病,则第一轮传染中感染2x人,第二轮传染中感染x(2+2x)人,
依题意得:,
即,
解得:,(不符合题意,舍去),
∴x的值为8.
故选:B.
5.答案:A
解析:∵、是关于x的一元二次方程的两个不相等的实数根,
∴,
解得:,
又∵,,,
∴,
∴
即
解得:或,
∵,
∴,
故选:A.
6.答案:D
解析:满足等式,
,解得,
,
,
解得,,
关于y的一元二次方程的根都是整数,且,m是整数,
或-2或-4,
满足条件的所有整数m的和是.
故选D.
7.答案:A
解析:设运动时间为t,
∵在中,,,,点P沿边从点A出发向终点B以的速度移动;同时点Q沿边从点B出发向终点C以的速度移动,
∴,,
∵的面积为,
∴,
解得:,,
∵点P在上的运动时间为:,
∴,
∴不符合题意,
∴点P的运动时间为,的面积为,故A正确,符合题意.
故选:A.
8.答案:B
解析:关于的方程有实数根,方程的两根分别是、,
,,
,
,
,
,
整理得:,
解得,
,
,
故选:B.
9.答案:
解析:依题意得,,
故答案为:.
10.答案:2012
解析:根据韦达定理可得:,,
∴原式.
故答案为:2012.
11.答案:5
解析:由题意可知,无盖纸盒的长为,宽为,
∴,
整理得,
解得,(不合题意,舍去),
故x的值为5.
故答案为:5.
12.答案:①是
②或
解析:(1),
,
解得,
,
方程是“倍根方程”.
故答案为:是;
(2)解方程得,
是“倍根方程”,
或,
故答案为:或.
13.答案:(1)
(2)能,
解析:(1)(件).
故答案为:;
(2)设每件衬衫降价x元,则每件盈利元,每天可以售出件,
依题意得:,
整理得:,
解得:,.
又∵每件盈利不少于25元,即,
,
.
答:当每件商品降价10元时,即,该商店每天销售利润为1200元.
14.答案:(1)k的取值范围为
(2)k的值为0或
解析:(1)方程化为一般式为,
根据题意得,解得,
即k的取值范围为;
(2)根据根与系数的关系得,,
∵,
∴,
∴,
∴,整理得,
解得,,
∵,
∴k的值为0或.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
