湘教版数学八年级上册 复习课件:2.2《命题与证明》(共13张PPT)
文档属性
| 名称 | 湘教版数学八年级上册 复习课件:2.2《命题与证明》(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 265.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-22 00:00:00 | ||
图片预览



文档简介
课件13张PPT。命题与证明
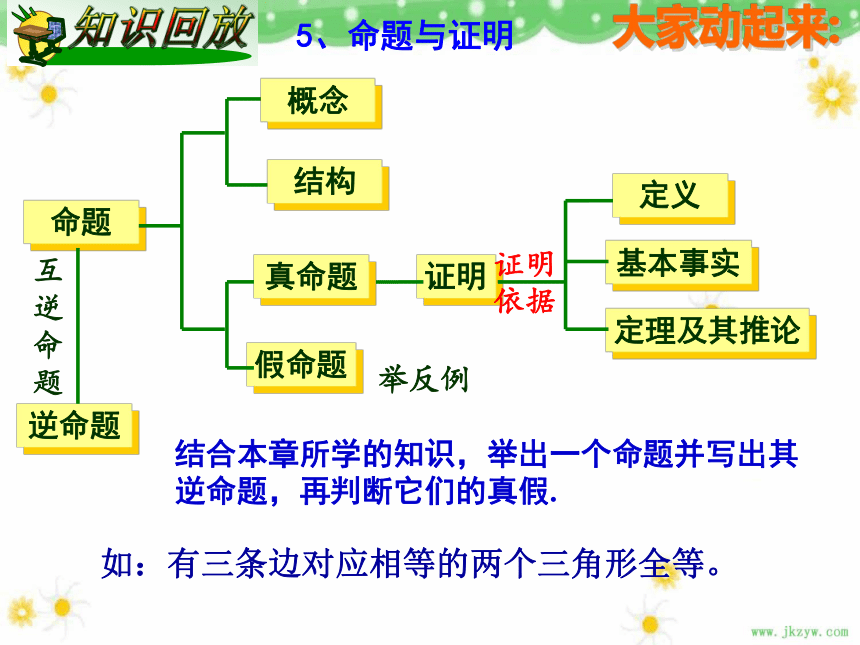
逆命题命题真命题假命题基本事实定理及其推论定义举反例证明证明
依据结合本章所学的知识,举出一个命题并写出其逆命题,再判断它们的真假.5、命题与证明概念结构大家动起来:如:有三条边对应相等的两个三角形全等。 “周长相等的两个三角形全等”是不是命题?如果是
命题,把它改写成“如果……,那么……”的形式,
并写出其逆命题。判断它们是真命题还是假命题?审题 :本题的要求是什么?题设、结论是什么?答:是命题.如果两个三角形的周长相等,那么这两个三角形全等。因为它不符合两个三角形全等的判定,所以它是假命题.如果两个三角形全等,那么这两个三角形的周长相等。(真命题)1. 一个命题是真命题,它的逆命题不一定是真命题.2. 命题有真有假. 要判断一个命题为真命题,需要
进行证明,并且证明的过程要言必有据.要判断一
个命题为假命题,只需举一个反例.1.下列句子中,哪些是命题?若是命题,并判断
它是真命题还是假命题?
(1)猴子是动物的一种; (2)美丽的天空;
(3)等角的余角相等; (4)同位角相等;
(5)负数都小于零; (6)若xy=0,则x=0;
(7)你的作业做完了吗?(8)所有质数都是奇数;
(9)三个角对应相等的两个三角形一定全等.
(10)过直线a外一点作直线a的平行线.
(11)两条直线相交,只有一个交点.
(12)如果一个数是偶数,那么这个数是4的倍数;2.命题“a,b是实数,若……,则a2>b2.”命题
的结论保持不变,改变命题的条件,有下列四种改法:
① a,b是实数,若a>b>0,则a2>b2;
② a,b是实数,若a>b,且a+b>0,则a2>b2;
③ a,b是实数,若ab2;
④ a,b是实数,若ab2.
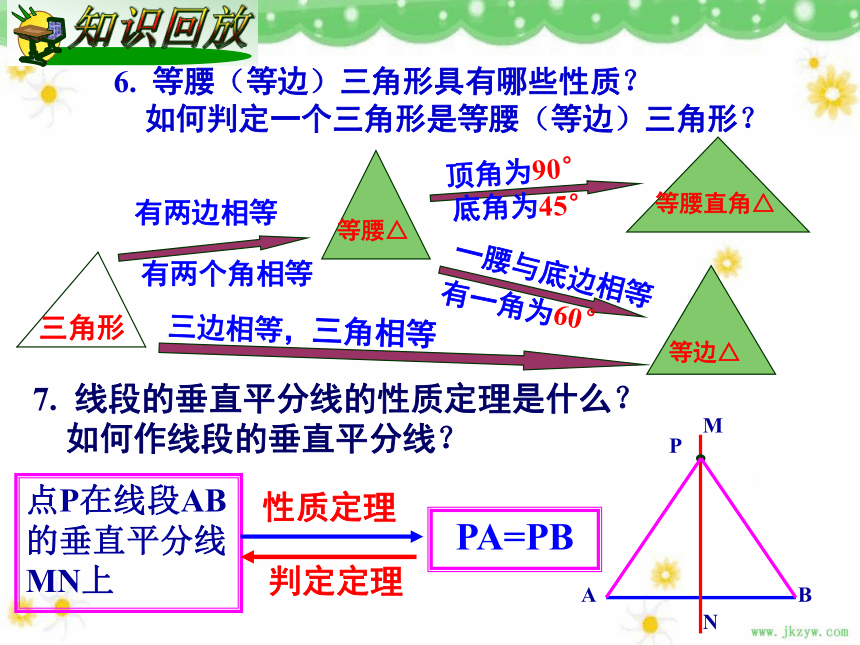
以上哪几个是真命题?请说明理由.6. 等腰(等边)三角形具有哪些性质?
如何判定一个三角形是等腰(等边)三角形?7. 线段的垂直平分线的性质定理是什么?
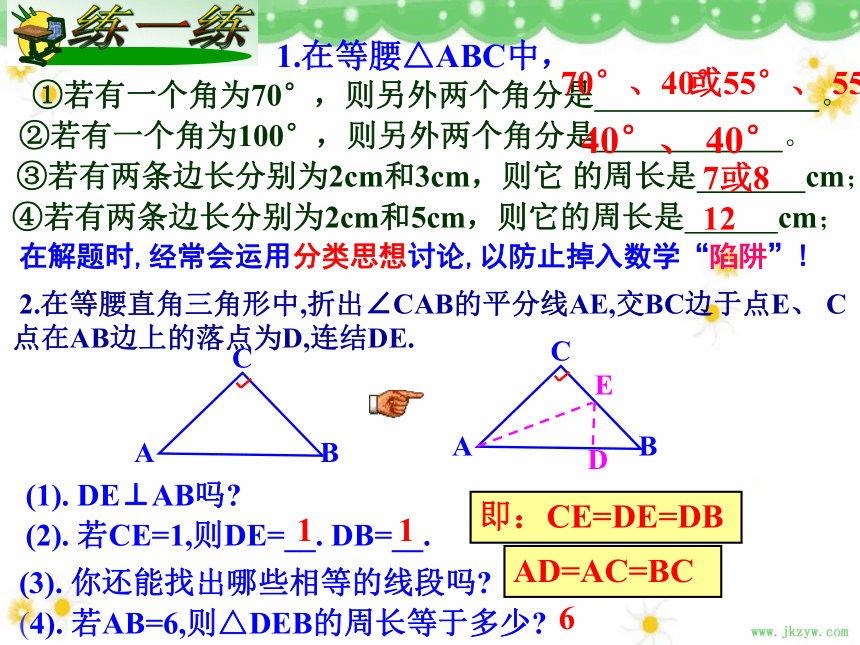
如何作线段的垂直平分线?有两边相等有两个角相等顶角为90°底角为45°一腰与底边相等有一角为60°三边相等,三角相等PA=PB点P在线段AB的垂直平分线MN上性质定理判定定理或55°、 55°1.在等腰△ABC中, ③若有两条边长分别为2cm和3cm,则它 的周长是 cm;①若有一个角为70°,则另外两个角分是 。 70°、40°②若有一个角为100°,则另外两个角分是 。 ④若有两条边长分别为2cm和5cm,则它的周长是 cm;40°、 40°7或812在解题时,经常会运用分类思想讨论,以防止掉入数学“陷阱”! 2.在等腰直角三角形中,折出∠CAB的平分线AE,交BC边于点E、 C点在AB边上的落点为D,连结DE.(1). DE⊥AB吗?(2). 若CE=1,则DE=__. DB=__.(3). 你还能找出哪些相等的线段吗? (4). 若AB=6,则△DEB的周长等于多少?11 6AD=AC=BC即:CE=DE=DB3.若等腰直角三角形两底角的平分线AO与BO交于点O,过O作底边AB的平行线EF,交AC于E,交BC于F。(1)则图中有几个等腰三角形?(2)AE,EF,BF之间的长度有何关系?(3)若AC=12,则ΔCEF的周长为多少?AE+BF=EF(24)ΔCEF的周长=AC+BC=20(4)若把等腰RtΔABC改为一般三角形,其他条件不变,当AC=12,BC=8时你能求ΔCEF的周长吗?相等角之间的转化相等线段之间的转化转化思想1.角与角的转化: 相等角之间的代换.
2.边与边的转化: 相等线段之间的代换
3.边与角的转化: 等边对等角.
等角对等边。(在同一个三角形)方程思想4.如图,在等腰△ABC中,AB=AC ,BD是△ABC 的角平分线,且AD=BD=BC,求∠A的度数.解:设∠BDC=x则∠A=x,∠ABC=∠ACB=2xx+2x+2x=180°x=36° ∴∠A=36° 求较复杂图形中角的度数
求较复杂图形中线段的长5.已知等腰三角形一腰上的中线将三角形周长分成2:1两部分,已知三角形底边长为10,求腰长?解:如图,设CD=x,则AD=x,AB=2x∵底边BC=10∴BC+CD=10+x AB+AD=3x∴10+x =2· 3x 解得x=2(舍去)或2 · (10+x)=3x 解得x=20(符合)∴ x=20,此时腰长40通过本堂课的探索,你有何收获?
2. 反思一下你所获成功的经验, 与同学交流! 数学知识: “等边对等角” 、“等角对等边”及“三线合一”
(在同一个三角形)
数学思想: 转化思想、方程思想、分类思想! 体会·分享1、如果等腰三角形的一个外角为100°,则这个等腰三角形的顶角为 。20°或80°2、如图,在三角形ABC中,BC=10,AD=BD,若三角形ACD的周长为18 , 则AC长为 。103、如图,在⊿ABC上,已知点D在BC上,
且BD+AD=BC.点D在AC的 .垂直平分线上例1:在ΔABC中,AB=2AC,∠1=∠2,DA=DB
求证:DC⊥ACF ∵DA=DB, AE=BE ∴DE⊥AB(等腰三角形三线合一)
∵AB=2AC, E为AB的中点 ∴AE=AC
在ΔAED和ΔACD中,
AE=AC,∠1=∠2, AD=AD ∴ΔAED≌ΔACD(SAS)
∴∠AED=∠ACD=900 即AC⊥DC延长法截短法∵AB=2AC,AC=C ∴AB=AF
∵∠1=∠2,AD=AD ∴ΔADB≌ΔADF(SAS)
∴DB=BF ∵DA=DB ∴DA=DF
∵AC=CF ∴DC⊥AF(等腰三角形三线合一)
即DC⊥AC通常作底边的中线或高或顶角平分线,
以便使用等腰三角形的性质(三线合一).·E名题探究证明(一):取AB的中点E,连结DE 证明(二):延长AC至F使CF=AC,连结DF例2:如图,ΔABC,ΔCDE是等边三角形
(1)求证:AE=BD(2)若BD和AC交于点M,AE和CD
交于点N,求证:CM=CNMN(3)连结MN,猜想MN与BE的位置关系.并加以证明思路探究:通过证明三角形全等从而证明线段相等或角相等,这是一种常见的证明方法.本题我们应注意用到等边三角形的性质以及平行法的判定方法.当图形较复杂时,注意分清条件与图形中的对应关系。证:ΔACE≌ΔBDE证:ΔBMC≌ΔANC由(2)得ΔMCN是等边三角形。
∴∠AMN=120°=∠ACE ∴MN∥BE例3.(1).求证:如果三角形一个外角的平分线平行于三角形的第三边,那么这个三角形是等腰三角形。(2).求证:等腰三角形两底角的平分线相等。思路:画图,写已知、求证,再证明。1、如图,AB=AC,∠A=40°,AB的垂直平分线MN交于点D,
求∠DBC的度数。4、如图,已知AD=BC,AC=BD,求证:△EAB是
等腰三角形。2、如图,DE是△ABC的边AB的垂直平分线,分别交AB、
AE平分∠BAC,若∠B=30°,求∠C的度数.3、已知,点P在∠AOB内,点M、N分别是点P关于OA、OB的对称点。连结M、N,分别交OA、OB于E、F,若MN=8cm,求三角形PEF的周长。1题2题3题4题5、如右上图,⊿ABC中,AB=AC,过BC上的一点D作BC的垂线
交AC于Q,交BA的延长线于P,试判断⊿APQ的形状,并说明理由。6、如图,P是∠AOB的平分线OM上任意一点,PE⊥OA于E,
PF⊥OB于F,连求证:OP垂直平分EF .7、如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,求证:△AEG的周长等于BC长。8、已知:如图,△ABC为正三角形,D是BC延长线上一点,连结AD,以AD为边作等边三角形ADE,连结CE,
用你学过的知识探索AC、CD、CE三条线段的长度有何关系?试写出探求过程.5题6题7题8题
逆命题命题真命题假命题基本事实定理及其推论定义举反例证明证明
依据结合本章所学的知识,举出一个命题并写出其逆命题,再判断它们的真假.5、命题与证明概念结构大家动起来:如:有三条边对应相等的两个三角形全等。 “周长相等的两个三角形全等”是不是命题?如果是
命题,把它改写成“如果……,那么……”的形式,
并写出其逆命题。判断它们是真命题还是假命题?审题 :本题的要求是什么?题设、结论是什么?答:是命题.如果两个三角形的周长相等,那么这两个三角形全等。因为它不符合两个三角形全等的判定,所以它是假命题.如果两个三角形全等,那么这两个三角形的周长相等。(真命题)1. 一个命题是真命题,它的逆命题不一定是真命题.2. 命题有真有假. 要判断一个命题为真命题,需要
进行证明,并且证明的过程要言必有据.要判断一
个命题为假命题,只需举一个反例.1.下列句子中,哪些是命题?若是命题,并判断
它是真命题还是假命题?
(1)猴子是动物的一种; (2)美丽的天空;
(3)等角的余角相等; (4)同位角相等;
(5)负数都小于零; (6)若xy=0,则x=0;
(7)你的作业做完了吗?(8)所有质数都是奇数;
(9)三个角对应相等的两个三角形一定全等.
(10)过直线a外一点作直线a的平行线.
(11)两条直线相交,只有一个交点.
(12)如果一个数是偶数,那么这个数是4的倍数;2.命题“a,b是实数,若……,则a2>b2.”命题
的结论保持不变,改变命题的条件,有下列四种改法:
① a,b是实数,若a>b>0,则a2>b2;
② a,b是实数,若a>b,且a+b>0,则a2>b2;
③ a,b是实数,若a
④ a,b是实数,若a
以上哪几个是真命题?请说明理由.6. 等腰(等边)三角形具有哪些性质?
如何判定一个三角形是等腰(等边)三角形?7. 线段的垂直平分线的性质定理是什么?
如何作线段的垂直平分线?有两边相等有两个角相等顶角为90°底角为45°一腰与底边相等有一角为60°三边相等,三角相等PA=PB点P在线段AB的垂直平分线MN上性质定理判定定理或55°、 55°1.在等腰△ABC中, ③若有两条边长分别为2cm和3cm,则它 的周长是 cm;①若有一个角为70°,则另外两个角分是 。 70°、40°②若有一个角为100°,则另外两个角分是 。 ④若有两条边长分别为2cm和5cm,则它的周长是 cm;40°、 40°7或812在解题时,经常会运用分类思想讨论,以防止掉入数学“陷阱”! 2.在等腰直角三角形中,折出∠CAB的平分线AE,交BC边于点E、 C点在AB边上的落点为D,连结DE.(1). DE⊥AB吗?(2). 若CE=1,则DE=__. DB=__.(3). 你还能找出哪些相等的线段吗? (4). 若AB=6,则△DEB的周长等于多少?11 6AD=AC=BC即:CE=DE=DB3.若等腰直角三角形两底角的平分线AO与BO交于点O,过O作底边AB的平行线EF,交AC于E,交BC于F。(1)则图中有几个等腰三角形?(2)AE,EF,BF之间的长度有何关系?(3)若AC=12,则ΔCEF的周长为多少?AE+BF=EF(24)ΔCEF的周长=AC+BC=20(4)若把等腰RtΔABC改为一般三角形,其他条件不变,当AC=12,BC=8时你能求ΔCEF的周长吗?相等角之间的转化相等线段之间的转化转化思想1.角与角的转化: 相等角之间的代换.
2.边与边的转化: 相等线段之间的代换
3.边与角的转化: 等边对等角.
等角对等边。(在同一个三角形)方程思想4.如图,在等腰△ABC中,AB=AC ,BD是△ABC 的角平分线,且AD=BD=BC,求∠A的度数.解:设∠BDC=x则∠A=x,∠ABC=∠ACB=2xx+2x+2x=180°x=36° ∴∠A=36° 求较复杂图形中角的度数
求较复杂图形中线段的长5.已知等腰三角形一腰上的中线将三角形周长分成2:1两部分,已知三角形底边长为10,求腰长?解:如图,设CD=x,则AD=x,AB=2x∵底边BC=10∴BC+CD=10+x AB+AD=3x∴10+x =2· 3x 解得x=2(舍去)或2 · (10+x)=3x 解得x=20(符合)∴ x=20,此时腰长40通过本堂课的探索,你有何收获?
2. 反思一下你所获成功的经验, 与同学交流! 数学知识: “等边对等角” 、“等角对等边”及“三线合一”
(在同一个三角形)
数学思想: 转化思想、方程思想、分类思想! 体会·分享1、如果等腰三角形的一个外角为100°,则这个等腰三角形的顶角为 。20°或80°2、如图,在三角形ABC中,BC=10,AD=BD,若三角形ACD的周长为18 , 则AC长为 。103、如图,在⊿ABC上,已知点D在BC上,
且BD+AD=BC.点D在AC的 .垂直平分线上例1:在ΔABC中,AB=2AC,∠1=∠2,DA=DB
求证:DC⊥ACF ∵DA=DB, AE=BE ∴DE⊥AB(等腰三角形三线合一)
∵AB=2AC, E为AB的中点 ∴AE=AC
在ΔAED和ΔACD中,
AE=AC,∠1=∠2, AD=AD ∴ΔAED≌ΔACD(SAS)
∴∠AED=∠ACD=900 即AC⊥DC延长法截短法∵AB=2AC,AC=C ∴AB=AF
∵∠1=∠2,AD=AD ∴ΔADB≌ΔADF(SAS)
∴DB=BF ∵DA=DB ∴DA=DF
∵AC=CF ∴DC⊥AF(等腰三角形三线合一)
即DC⊥AC通常作底边的中线或高或顶角平分线,
以便使用等腰三角形的性质(三线合一).·E名题探究证明(一):取AB的中点E,连结DE 证明(二):延长AC至F使CF=AC,连结DF例2:如图,ΔABC,ΔCDE是等边三角形
(1)求证:AE=BD(2)若BD和AC交于点M,AE和CD
交于点N,求证:CM=CNMN(3)连结MN,猜想MN与BE的位置关系.并加以证明思路探究:通过证明三角形全等从而证明线段相等或角相等,这是一种常见的证明方法.本题我们应注意用到等边三角形的性质以及平行法的判定方法.当图形较复杂时,注意分清条件与图形中的对应关系。证:ΔACE≌ΔBDE证:ΔBMC≌ΔANC由(2)得ΔMCN是等边三角形。
∴∠AMN=120°=∠ACE ∴MN∥BE例3.(1).求证:如果三角形一个外角的平分线平行于三角形的第三边,那么这个三角形是等腰三角形。(2).求证:等腰三角形两底角的平分线相等。思路:画图,写已知、求证,再证明。1、如图,AB=AC,∠A=40°,AB的垂直平分线MN交于点D,
求∠DBC的度数。4、如图,已知AD=BC,AC=BD,求证:△EAB是
等腰三角形。2、如图,DE是△ABC的边AB的垂直平分线,分别交AB、
AE平分∠BAC,若∠B=30°,求∠C的度数.3、已知,点P在∠AOB内,点M、N分别是点P关于OA、OB的对称点。连结M、N,分别交OA、OB于E、F,若MN=8cm,求三角形PEF的周长。1题2题3题4题5、如右上图,⊿ABC中,AB=AC,过BC上的一点D作BC的垂线
交AC于Q,交BA的延长线于P,试判断⊿APQ的形状,并说明理由。6、如图,P是∠AOB的平分线OM上任意一点,PE⊥OA于E,
PF⊥OB于F,连求证:OP垂直平分EF .7、如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,求证:△AEG的周长等于BC长。8、已知:如图,△ABC为正三角形,D是BC延长线上一点,连结AD,以AD为边作等边三角形ADE,连结CE,
用你学过的知识探索AC、CD、CE三条线段的长度有何关系?试写出探求过程.5题6题7题8题
同课章节目录
