湘教版数学八年级上册 复习课件:2.5全等三角形判定(共13张PPT)
文档属性
| 名称 | 湘教版数学八年级上册 复习课件:2.5全等三角形判定(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-22 17:29:00 | ||
图片预览


文档简介
(共13张PPT)
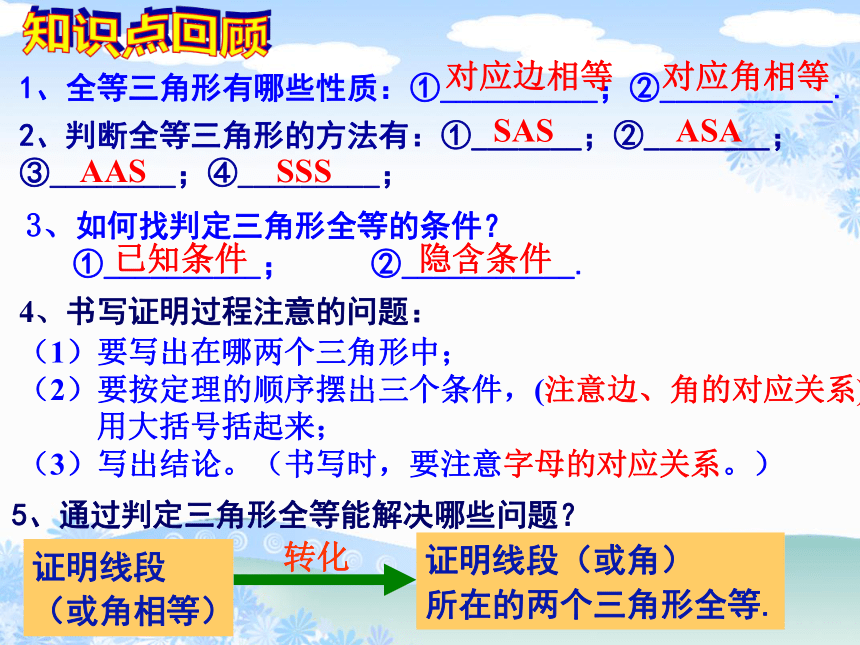
2、判断全等三角形的方法有:①_______;②________;
③________;④_________;
1、全等三角形有哪些性质:①__________;②___________.
3、如何找判定三角形全等的条件?
①__________; ②___________.
5、通过判定三角形全等能解决哪些问题?
证明线段
(或角相等)
证明线段(或角)
所在的两个三角形全等.
转化
4、书写证明过程注意的问题:
(1)要写出在哪两个三角形中;
(2)要按定理的顺序摆出三个条件,(注意边、角的对应关系)
用大括号括起来;
(3)写出结论。(书写时,要注意字母的对应关系。)
对应边相等
对应角相等
SAS
ASA
AAS
SSS
已知条件
隐含条件
讲练结合
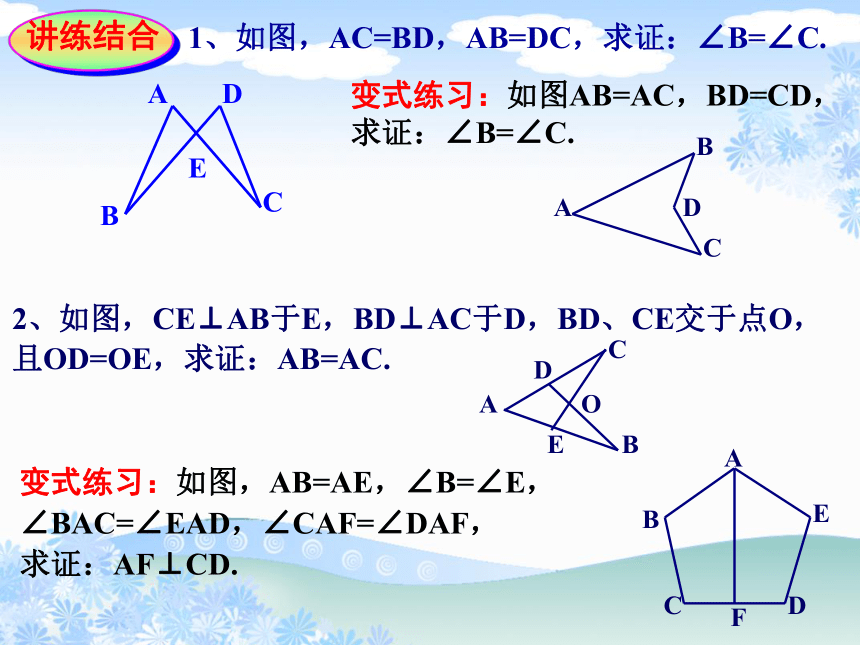
1、如图,AC=BD,AB=DC,求证:∠B=∠C.
变式练习:如图AB=AC,BD=CD,
求证:∠B=∠C.
A
B
C
D
E
A
D
C
B
2、如图,CE⊥AB于E,BD⊥AC于D,BD、CE交于点O,
且OD=OE,求证:AB=AC.
变式练习:如图,AB=AE,∠B=∠E,
∠BAC=∠EAD,∠CAF=∠DAF,
求证:AF⊥CD.
A
B
C
D
E
O
A
B
C
D
E
F
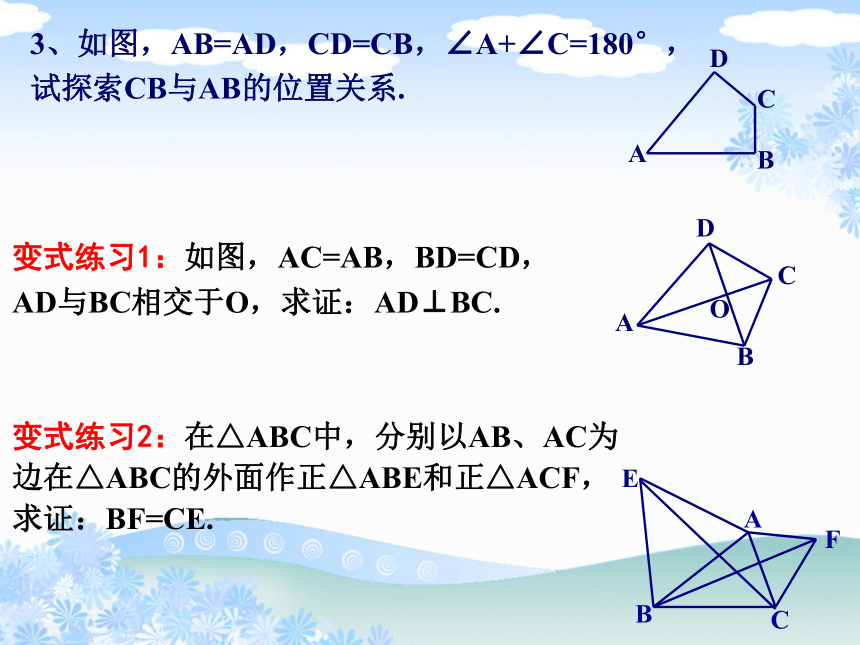
3、如图,AB=AD,CD=CB,∠A+∠C=180°,
试探索CB与AB的位置关系.
变式练习1:如图,AC=AB,BD=CD,
AD与BC相交于O,求证:AD⊥BC.
变式练习2:在△ABC中,分别以AB、AC为边在△ABC的外面作正△ABE和正△ACF,
求证:BF=CE.
A
B
C
D
A
B
C
D
O
A
B
C
E
F
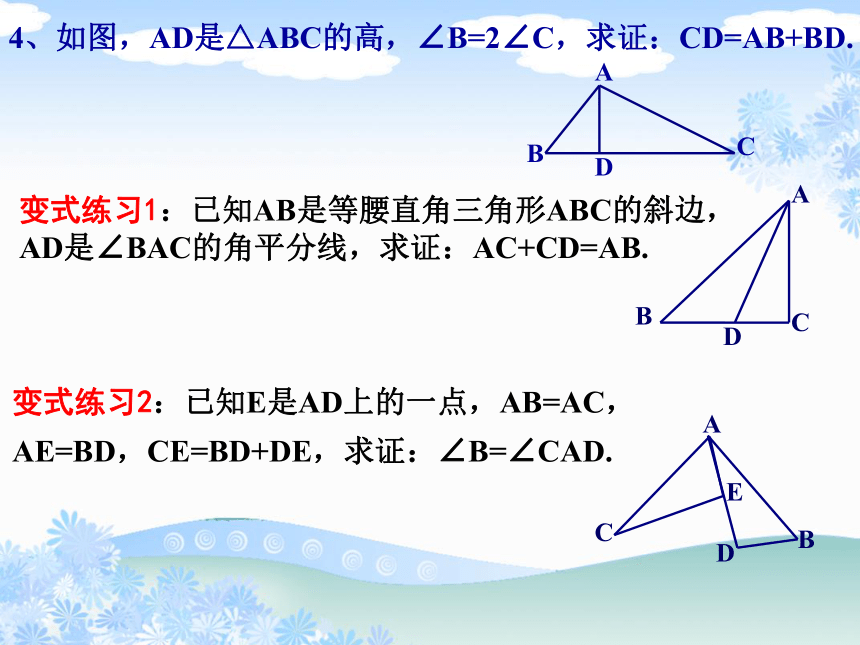
变式练习2:已知E是AD上的一点,AB=AC,AE=BD,CE=BD+DE,求证:∠B=∠CAD.
4、如图,AD是△ABC的高,∠B=2∠C,求证:CD=AB+BD.
A
B
C
D
变式练习1:已知AB是等腰直角三角形ABC的斜边,
AD是∠BAC的角平分线,求证:AC+CD=AB.
A
B
C
D
A
B
C
D
E
5、在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,
如图,且AD⊥MN于D,BE⊥MN于E,求证:DE=AD-BE.
变式练习2:如图,AB=AC,∠BAC=900,
BD⊥AE于D,CE⊥AE于E,且BD>CE,
求证:BD=EC+ED.
变式练习1:在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,如图,且AD⊥MN于D,BE⊥MN于E,
求证:DE=AD+BE.
A
B
C
D
E
M
N
A
B
C
D
E
M
N
A
B
C
D
E
6、在△ABC中,AB=AC,在AB上取一
点D,在AC的延长线上取一点E,使
BD=CE,连结DE交BC于点F,
求证:DF=EF.
变式练习:在△ABC中,AB=AC,在AB上取一点D,在AC的延长线上取一点E,连结DE交BC
于点F,若DF=EF,
求证:BD=CE.
A
B
C
D
E
F
7、如图,OA=OB,C、D分别是OA,
OB上的两点,且OC=OD,连结AD、
BC交于点E,
求证:OE平分∠AOB.
变式练习:如图,AB=AC,D是
∠BAC平分线上的一点,连结
CD并延长交AB于点E,连结BD
并延长交AC于点F,
求证:AE=AF.
A
B
C
O
D
E
A
B
C
D
E
F
中考
试题
1、已知:在△ABC中,AC=BC,∠ACB=900,
点D是AB的中点,点E是AB边上一点.
A
B
C
D
E
F
G
(1)
A
B
C
D
E
H
M
(2)
(1)直线BF垂直于CE于点F,交CD于点G(如图①),
求证:AE=CG;
(2)直线AH垂直CE,垂足为H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.
证明△AEC≌△CGB
证明△BCE≌△CMA
求证:BE=CM
2.如图,已知点D为等腰直角△ABC内一点,。∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
(1)求证:DE平分∠BDC;
证明:在等腰直角△ABC中,
∵∠CAD=∠CBD=15o,
∴∠BAD=∠ABD=45o-15o=30o,
∴BD=AD,∴△BDC≌△ADC,
∴∠DCA=∠DCB=45o.
由∠BDM=∠ABD+∠BAD=30o+30o=60o,
∠EDC=∠DAC+∠DCA=15o+45o=60o,
∴∠BDM=∠EDC,
∴DE平分∠BDC;
证明:如图,连接MC,
∵DC=DM,且∠MDC=60°,
∴△MDC是等边三角形,即CM=CD.
又∵∠EMC=180°-∠DMC=180°-60°=120°,
∠ADC=180°-∠MDC=180°-60°=120°,
∴∠EMC=∠ADC.
又∵CE=CA,
∴∠DAC=∠CEM=15°,
∴△ADC≌△EMC,
∴ME=AD=DB.
(2)若点M在DE上,且DC=DM,求证: ME=BD.
1.已知∠1 = ∠2,∠3 = ∠4,问AC=AD吗?
说明理由。
2.已知ED⊥AB,EF⊥BC,BD = EF,问BM = ME吗?
说明理由。
3.在△ABC中,高AD与BE相交于点H,且AD = BD,
问△BHD≌ △ACD,为什么?
4.已知AC = AB,AE = AD, ∠1 = ∠2,问∠3 =∠4吗?
练 习
A
B
C
D
1
2
3
4
1题
A
B
C
D
E
F
M
2题
A
B
C
D
E
H
3题
1
2
3
4
A
B
C
D
E
4题
5.已知∠1 =∠2,BC = AD,求证:AC=BD
6.已知AD = AE,BD = CE,求证:△ABC是等腰三角形。
7.已知∠1 =∠2,AC = BD,E,F,A,B在同一直线上,
求证:∠CAD =∠DBC
8.已知:如图,∠A =∠D = 90°,AC,BD交于O,
AC = BD,求证:OB = OC.
1
1
2
A
B
C
D
O
5题
1
2
A
B
C
D
E
6题
1
2
3
4
A
B
C
D
E
F
7题
A
B
C
D
O
8题
2、判断全等三角形的方法有:①_______;②________;
③________;④_________;
1、全等三角形有哪些性质:①__________;②___________.
3、如何找判定三角形全等的条件?
①__________; ②___________.
5、通过判定三角形全等能解决哪些问题?
证明线段
(或角相等)
证明线段(或角)
所在的两个三角形全等.
转化
4、书写证明过程注意的问题:
(1)要写出在哪两个三角形中;
(2)要按定理的顺序摆出三个条件,(注意边、角的对应关系)
用大括号括起来;
(3)写出结论。(书写时,要注意字母的对应关系。)
对应边相等
对应角相等
SAS
ASA
AAS
SSS
已知条件
隐含条件
讲练结合
1、如图,AC=BD,AB=DC,求证:∠B=∠C.
变式练习:如图AB=AC,BD=CD,
求证:∠B=∠C.
A
B
C
D
E
A
D
C
B
2、如图,CE⊥AB于E,BD⊥AC于D,BD、CE交于点O,
且OD=OE,求证:AB=AC.
变式练习:如图,AB=AE,∠B=∠E,
∠BAC=∠EAD,∠CAF=∠DAF,
求证:AF⊥CD.
A
B
C
D
E
O
A
B
C
D
E
F
3、如图,AB=AD,CD=CB,∠A+∠C=180°,
试探索CB与AB的位置关系.
变式练习1:如图,AC=AB,BD=CD,
AD与BC相交于O,求证:AD⊥BC.
变式练习2:在△ABC中,分别以AB、AC为边在△ABC的外面作正△ABE和正△ACF,
求证:BF=CE.
A
B
C
D
A
B
C
D
O
A
B
C
E
F
变式练习2:已知E是AD上的一点,AB=AC,AE=BD,CE=BD+DE,求证:∠B=∠CAD.
4、如图,AD是△ABC的高,∠B=2∠C,求证:CD=AB+BD.
A
B
C
D
变式练习1:已知AB是等腰直角三角形ABC的斜边,
AD是∠BAC的角平分线,求证:AC+CD=AB.
A
B
C
D
A
B
C
D
E
5、在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,
如图,且AD⊥MN于D,BE⊥MN于E,求证:DE=AD-BE.
变式练习2:如图,AB=AC,∠BAC=900,
BD⊥AE于D,CE⊥AE于E,且BD>CE,
求证:BD=EC+ED.
变式练习1:在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,如图,且AD⊥MN于D,BE⊥MN于E,
求证:DE=AD+BE.
A
B
C
D
E
M
N
A
B
C
D
E
M
N
A
B
C
D
E
6、在△ABC中,AB=AC,在AB上取一
点D,在AC的延长线上取一点E,使
BD=CE,连结DE交BC于点F,
求证:DF=EF.
变式练习:在△ABC中,AB=AC,在AB上取一点D,在AC的延长线上取一点E,连结DE交BC
于点F,若DF=EF,
求证:BD=CE.
A
B
C
D
E
F
7、如图,OA=OB,C、D分别是OA,
OB上的两点,且OC=OD,连结AD、
BC交于点E,
求证:OE平分∠AOB.
变式练习:如图,AB=AC,D是
∠BAC平分线上的一点,连结
CD并延长交AB于点E,连结BD
并延长交AC于点F,
求证:AE=AF.
A
B
C
O
D
E
A
B
C
D
E
F
中考
试题
1、已知:在△ABC中,AC=BC,∠ACB=900,
点D是AB的中点,点E是AB边上一点.
A
B
C
D
E
F
G
(1)
A
B
C
D
E
H
M
(2)
(1)直线BF垂直于CE于点F,交CD于点G(如图①),
求证:AE=CG;
(2)直线AH垂直CE,垂足为H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.
证明△AEC≌△CGB
证明△BCE≌△CMA
求证:BE=CM
2.如图,已知点D为等腰直角△ABC内一点,。∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
(1)求证:DE平分∠BDC;
证明:在等腰直角△ABC中,
∵∠CAD=∠CBD=15o,
∴∠BAD=∠ABD=45o-15o=30o,
∴BD=AD,∴△BDC≌△ADC,
∴∠DCA=∠DCB=45o.
由∠BDM=∠ABD+∠BAD=30o+30o=60o,
∠EDC=∠DAC+∠DCA=15o+45o=60o,
∴∠BDM=∠EDC,
∴DE平分∠BDC;
证明:如图,连接MC,
∵DC=DM,且∠MDC=60°,
∴△MDC是等边三角形,即CM=CD.
又∵∠EMC=180°-∠DMC=180°-60°=120°,
∠ADC=180°-∠MDC=180°-60°=120°,
∴∠EMC=∠ADC.
又∵CE=CA,
∴∠DAC=∠CEM=15°,
∴△ADC≌△EMC,
∴ME=AD=DB.
(2)若点M在DE上,且DC=DM,求证: ME=BD.
1.已知∠1 = ∠2,∠3 = ∠4,问AC=AD吗?
说明理由。
2.已知ED⊥AB,EF⊥BC,BD = EF,问BM = ME吗?
说明理由。
3.在△ABC中,高AD与BE相交于点H,且AD = BD,
问△BHD≌ △ACD,为什么?
4.已知AC = AB,AE = AD, ∠1 = ∠2,问∠3 =∠4吗?
练 习
A
B
C
D
1
2
3
4
1题
A
B
C
D
E
F
M
2题
A
B
C
D
E
H
3题
1
2
3
4
A
B
C
D
E
4题
5.已知∠1 =∠2,BC = AD,求证:AC=BD
6.已知AD = AE,BD = CE,求证:△ABC是等腰三角形。
7.已知∠1 =∠2,AC = BD,E,F,A,B在同一直线上,
求证:∠CAD =∠DBC
8.已知:如图,∠A =∠D = 90°,AC,BD交于O,
AC = BD,求证:OB = OC.
1
1
2
A
B
C
D
O
5题
1
2
A
B
C
D
E
6题
1
2
3
4
A
B
C
D
E
F
7题
A
B
C
D
O
8题
同课章节目录
