湘教版数学八年级上册 课件:2.1《三角形有关概念》(共13张PPT)
文档属性
| 名称 | 湘教版数学八年级上册 课件:2.1《三角形有关概念》(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 533.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-22 16:48:13 | ||
图片预览



文档简介
课件13张PPT。三角形
的有关概念三
角
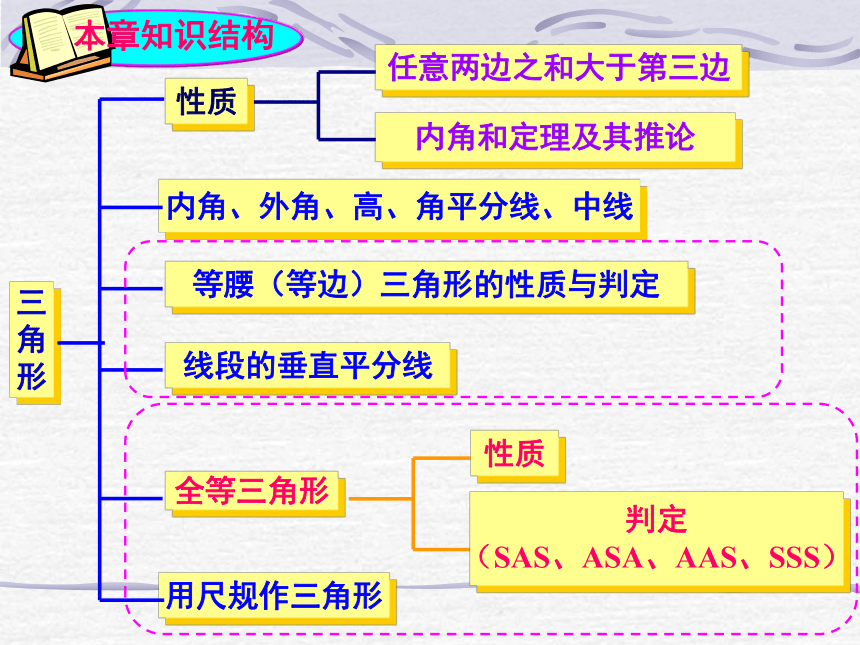
形内角、外角、高、角平分线、中线性质等腰(等边)三角形的性质与判定线段的垂直平分线全等三角形用尺规作三角形任意两边之和大于第三边内角和定理及其推论性质判定
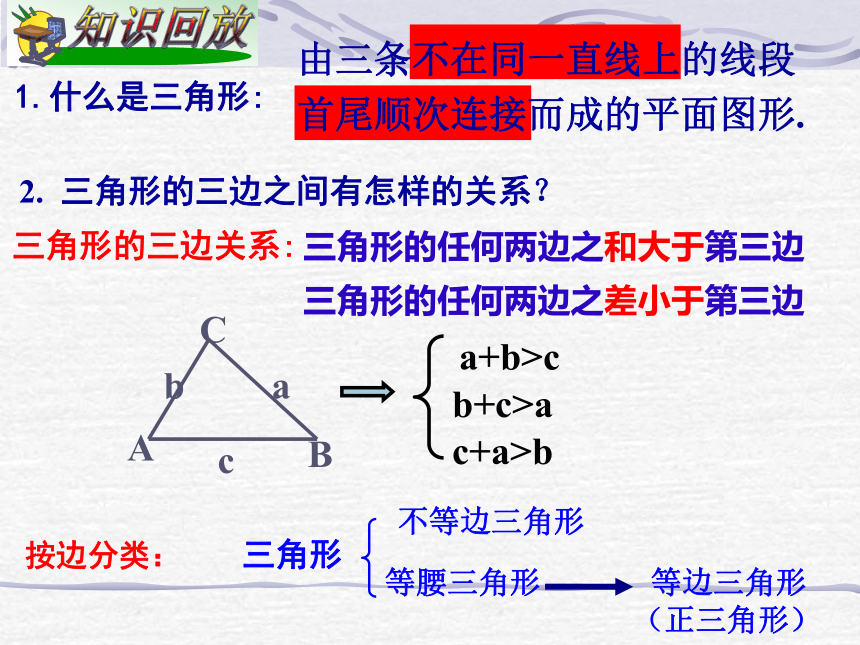
(SAS、ASA、AAS、SSS)1.什么是三角形:由三条不在同一直线上的线段首尾顺次连接而成的平面图形.2. 三角形的三边之间有怎样的关系?三角形的三边关系:三角形的任何两边之和大于第三边a+b>cb+c>ac+a>b三角形的任何两边之差小于第三边按边分类:三角形 不等边三角形1.长度为6cm,4cm,3cm三条线段能否组成三角形?2.下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm3.现有木棒4根,长度分别为12, 10, 8, 4, 选其中3根组成三角形,则能组成三角形的个数是( )
A.1 B.2 C.3 D.4C4.已知等腰三角形两条边长分别为3cm、5cm,则三角形的周长 . 2cm5.已知三角形的两边a,b长分别为2和3,则第三边c的范围
是 。12、三角形的一个外角等于和它不相邻的两个内角的和。
3、三角形的外角和等于360°。如图所示,AD是∠BAC的平分线,并且∠ADC=∠ACD=65°,求∠B、∠BAC的度数。解: ∵∠ADC=∠ACD=65°
∴∠DAC=180°-65°-65°=50°
∵AD平分∠BAC
∴∠BAC=2∠DAC=100°
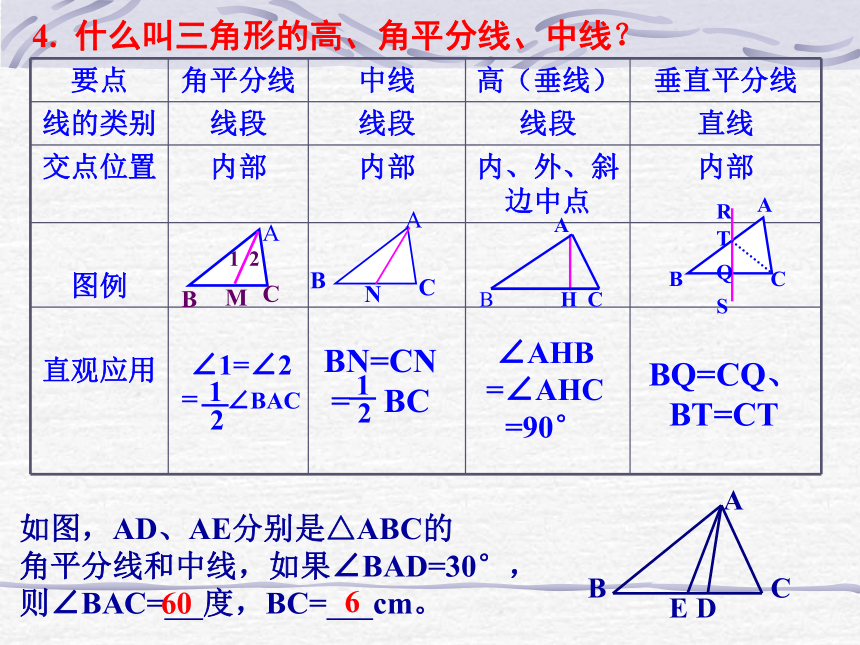
∴∠B=180°-∠BAC-∠ACD=180°-100°-65°=15°按角分类:三角形 锐角三角形斜三角形 钝三角形直角三角形4. 什么叫三角形的高、角平分线、中线?如图,AD、AE分别是△ABC的
角平分线和中线,如果∠BAD=30°,
则∠BAC= 度,BC= cm。60 6
∠AHB
=∠AHC
=90°BQ=CQ、
BT=CT 1.在⊿ABC中,AB=AC,CD平分∠ACB
交AB于点D,∠BDC=120o,
求∠A的度数。解:设∠ACD=x,则∠ABC=∠ACB=2x∴∠ABC+∠BCD=3x=60°x =20o =∠ACD∴∠A=120°-20°=100° 2.如图,在△ABC中,∠B=65°,∠C=45°, AD是BC边上的高 ,AE是∠BAC的平分线, 求∠DAE的度数。解:∵∠B=65°,∠C=45°,
∴∠BAC=70°∵AE是∠BA C的平分线,
∴∠BAE=35° ∵AD是BC边上的高 ,
∴∠BAD=90°-65°=25°∴∠DAE=∠BAE-∠BAD=35°-25°=10°2.小明有两根长度为6cm、9cm的木条,他想钉一个三角形的木框,现在有长度分别为2cm 、3cm、 8cm 、15cm的木条供他选择,那他应选( )
A、2cm B、3cm C、8cm D、15cm.DC3.下列长度的3条线段,首尾依次相接能组成三角形的是( )(A)1cm,2cm,4cm (B)8cm,6cm,4cm
(C)12cm,5cm,6cm (D)2cm,3cm,5cm4.一个三角形的两边分别为1.5和8.5,而第三边长是偶数,那么第三边为 。三角形的周长是 。5.一个等腰三角形的两边长分别是 4cm 和7cm,则它的周长是 . 6.一个三角形最多有 个直角,最多有 个钝角。
一个三角形最少有 个内角是锐角。1127.在⊿ABC中,∠A﹕∠B ﹕ ∠C= 1 ﹕ 1 ﹕ 2,
则∠A = ,∠B = , ∠C= ,
这个三角形是 三角形。45°45°90°等腰直角B81815cm或18cm8、在下图中30°40°60°60°70°9.如图,AB∥DC,AE⊥BC,垂足为E,∠BAE=30°,则∠B= , ∠C= .60°120°10.如图,AD平分∠BAC,其中∠B=50°,
∠ADC=80°求∠BAC、∠C的度数。
1.如图(1)中是一个五角星,你会求∠A+∠B+∠C+∠D+∠E的值吗?(2)图中的点A向下移到BE上时,五个角的和
(即∠CAD+∠B+∠C+∠D+∠E )有无变化?
如图(2)说明你的结论的正确性。(3)把图(2)中的点C向上移动到BD上时,
五个角的和( 即∠CAD+∠B+∠ACE+∠D+∠E )
有无变化?如图(3)说明你的结论的正确性。2.湖边有A,B两个村庄(如图),从A到B有两条
路可走,即A→P→B,和A→Q→B,哪条路短?
你能运用三角形三边关系说明理由吗?A→Q→B短课堂小结:1、知识结构三角形2、数学思想方法观察——探索——说理数形结合(图形与数量之间关系)化归思想(化复杂为简单,化未知为已知)作业:P97 A、B部分题
的有关概念三
角
形内角、外角、高、角平分线、中线性质等腰(等边)三角形的性质与判定线段的垂直平分线全等三角形用尺规作三角形任意两边之和大于第三边内角和定理及其推论性质判定
(SAS、ASA、AAS、SSS)1.什么是三角形:由三条不在同一直线上的线段首尾顺次连接而成的平面图形.2. 三角形的三边之间有怎样的关系?三角形的三边关系:三角形的任何两边之和大于第三边a+b>cb+c>ac+a>b三角形的任何两边之差小于第三边按边分类:三角形 不等边三角形1.长度为6cm,4cm,3cm三条线段能否组成三角形?2.下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm3.现有木棒4根,长度分别为12, 10, 8, 4, 选其中3根组成三角形,则能组成三角形的个数是( )
A.1 B.2 C.3 D.4C4.已知等腰三角形两条边长分别为3cm、5cm,则三角形的周长 . 2cm5.已知三角形的两边a,b长分别为2和3,则第三边c的范围
是 。1
3、三角形的外角和等于360°。如图所示,AD是∠BAC的平分线,并且∠ADC=∠ACD=65°,求∠B、∠BAC的度数。解: ∵∠ADC=∠ACD=65°
∴∠DAC=180°-65°-65°=50°
∵AD平分∠BAC
∴∠BAC=2∠DAC=100°
∴∠B=180°-∠BAC-∠ACD=180°-100°-65°=15°按角分类:三角形 锐角三角形斜三角形 钝三角形直角三角形4. 什么叫三角形的高、角平分线、中线?如图,AD、AE分别是△ABC的
角平分线和中线,如果∠BAD=30°,
则∠BAC= 度,BC= cm。60 6
∠AHB
=∠AHC
=90°BQ=CQ、
BT=CT 1.在⊿ABC中,AB=AC,CD平分∠ACB
交AB于点D,∠BDC=120o,
求∠A的度数。解:设∠ACD=x,则∠ABC=∠ACB=2x∴∠ABC+∠BCD=3x=60°x =20o =∠ACD∴∠A=120°-20°=100° 2.如图,在△ABC中,∠B=65°,∠C=45°, AD是BC边上的高 ,AE是∠BAC的平分线, 求∠DAE的度数。解:∵∠B=65°,∠C=45°,
∴∠BAC=70°∵AE是∠BA C的平分线,
∴∠BAE=35° ∵AD是BC边上的高 ,
∴∠BAD=90°-65°=25°∴∠DAE=∠BAE-∠BAD=35°-25°=10°2.小明有两根长度为6cm、9cm的木条,他想钉一个三角形的木框,现在有长度分别为2cm 、3cm、 8cm 、15cm的木条供他选择,那他应选( )
A、2cm B、3cm C、8cm D、15cm.DC3.下列长度的3条线段,首尾依次相接能组成三角形的是( )(A)1cm,2cm,4cm (B)8cm,6cm,4cm
(C)12cm,5cm,6cm (D)2cm,3cm,5cm4.一个三角形的两边分别为1.5和8.5,而第三边长是偶数,那么第三边为 。三角形的周长是 。5.一个等腰三角形的两边长分别是 4cm 和7cm,则它的周长是 . 6.一个三角形最多有 个直角,最多有 个钝角。
一个三角形最少有 个内角是锐角。1127.在⊿ABC中,∠A﹕∠B ﹕ ∠C= 1 ﹕ 1 ﹕ 2,
则∠A = ,∠B = , ∠C= ,
这个三角形是 三角形。45°45°90°等腰直角B81815cm或18cm8、在下图中30°40°60°60°70°9.如图,AB∥DC,AE⊥BC,垂足为E,∠BAE=30°,则∠B= , ∠C= .60°120°10.如图,AD平分∠BAC,其中∠B=50°,
∠ADC=80°求∠BAC、∠C的度数。
1.如图(1)中是一个五角星,你会求∠A+∠B+∠C+∠D+∠E的值吗?(2)图中的点A向下移到BE上时,五个角的和
(即∠CAD+∠B+∠C+∠D+∠E )有无变化?
如图(2)说明你的结论的正确性。(3)把图(2)中的点C向上移动到BD上时,
五个角的和( 即∠CAD+∠B+∠ACE+∠D+∠E )
有无变化?如图(3)说明你的结论的正确性。2.湖边有A,B两个村庄(如图),从A到B有两条
路可走,即A→P→B,和A→Q→B,哪条路短?
你能运用三角形三边关系说明理由吗?A→Q→B短课堂小结:1、知识结构三角形2、数学思想方法观察——探索——说理数形结合(图形与数量之间关系)化归思想(化复杂为简单,化未知为已知)作业:P97 A、B部分题
同课章节目录
