湘教版数学七年级上册 课件:3.1 《建立一元一次方程模型 》(共28张PPT)
文档属性
| 名称 | 湘教版数学七年级上册 课件:3.1 《建立一元一次方程模型 》(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 757.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-22 18:00:50 | ||
图片预览








文档简介
课件28张PPT。3.1 建立一元一次方程模型1.理解方程、一元一次方程和方程的解等概念,并会判断一个方程是否为一元一次方程.(重点)
2.会判断一个数是否为方程的解.(重点)
3.能从简单的实际问题中找出等量关系,并列出方程.(难点)一元一次方程及有关概念
1.含有_______的等式叫做方程.
2.建立方程:把所要求的量用字母x(或y,…)表示,根据问题
中的_____关系列出方程,这一过程叫做建立方程.
3.观察方程:2x=5,y+9=0, (x-1)=3x-6,2(26-x)=22+x.未知数等量【思考】(1)观察上面的四个方程,每个方程含有未知数的个数是多少?
提示:每个方程都含有1个未知数.
(2)每个未知数的次数分别是多少?
提示:每个未知数的次数都是1.
(3)等号两边的式子是整式吗?
提示:是.
【总结】一元一次方程的定义:只含有一个未知数,并且未知数的次数是1的整式方程叫做一元一次方程.4.方程的解:能使方程左、右两边_____的未知数的___.相等值 (打“√”或“×”)
(1)4x+7是方程.( )
(2)未知数的次数是一次的方程是一元一次方程.( )
(3)设某数为x,则另一个数比它的2倍多1可列方程:x-
2=1.( )
(4)3x+1= -1是一元一次方程.( )××××知识点 1 一元一次方程的有关概念
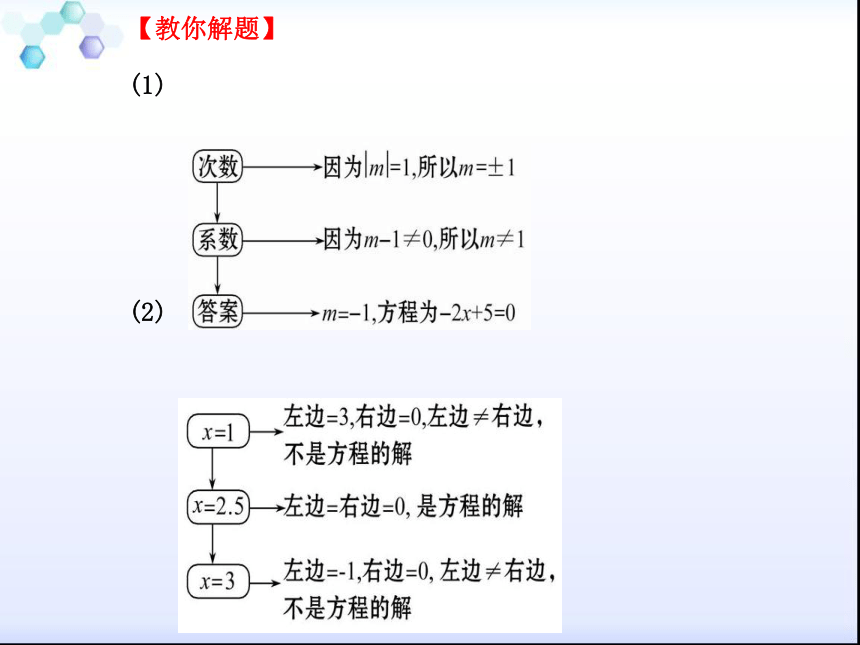
【例1】若(m-1)x|m|+5=0是关于x的一元一次方程.
(1)求m的值,并写出这个方程.
(2)判断x=1,x=2.5,x=3是否是方程的解.【教你解题】
(1)
(2)【总结提升】
1.判断一元一次方程的三个条件
(1)只含有一个未知数.
(2)未知数的次数是1.
(3)等号两边都是整式.2.判断方程解的三个步骤
(1)代:把所给未知数的值分别代入方程等号的左右两边.
(2)算:计算等号的左右两边的值.
(3)判:若左边=右边,则是方程的解;若左边≠右边,则不是方程的解.知识点 2 列一元一次方程
【例2】(湘潭中考)湖南省2011年赴台旅游人数达7.6万人.我市某九年级一学生家长准备中考后全家3人去台湾旅游,计划花费20 000元.设每人向旅行社缴纳x元费用后,共剩
5 000元用于购物和品尝台湾美食.根据题意,列出方程为_____.【解题探究】1.此题的等量关系是什么?
提示:全家向旅行社缴纳的费用+购物和品尝台湾美食的费用=总费用.
2.题目中一家3人共向旅行社缴纳费用多少?
提示:3x元.
3.此题中的购物和品尝台湾美食的费用和总费用分别为多少元?
提示:5 000元和20 000元.
4.综上根据等量关系列出的方程是________________.3x+5 000=20 000【互动探究】此题中的等量关系还可以是什么?
提示:每人向旅行社缴纳的费用【总结提升】列方程的三个步骤
1.设:恰当地设未知数.
2.找:找出能表示应用题全部含义的一个等量关系.
3.列:根据等量关系列出方程.题组一:一元一次方程的有关概念
1.下列方程为一元一次方程的是( )
A.x+5=y+4 B.
C.x2-x=1 D.x=0
【解析】选D.选项A有两个未知数;选项B中的 不是整式;
选项C中未知数的最高次数是2,故A,B,C都不是一元一次方
程,选项D符合一元一次方程的定义.2.下列方程中,解为x=3的是( )
A.6x=2 B.3x-9=0
C. x=0 D.5x+15=0
【解析】选B.把x=3分别代入四个方程,只有方程3x-9=0左右两边相等.3.(2012·重庆中考)关于x的方程2x+a-9=0的解是x=2,则a的值为( )
A.2 B.3 C.4 D.5
【解析】选D.把x=2代入方程2x+a-9=0得2×2+a-9=0,所以a=5.4.关于x的方程xn-1+5=0是一元一次方程,求n的值.
【解析】由题意n-1=1,故n=2.5.已知y=1是方程my=y+2的解,求m2-3m+1的值.
【解析】因为y=1是方程my=y+2的解,
所以m=1+2,故m=3,
当m=3时,m2-3m+1=9-3×3+1=1.题组二:列一元一次方程
1.小悦买书需用48元钱,付款时恰好用了1元和5元的纸币共12张.设所用的1元纸币为x张,根据题意,下面所列方程正确的是( )
A.x+5(12-x)=48 B.x+5(x-12)=48
C.x+12(x-5)=48 D.5x+(12-x)=48
【解析】选A.1元纸币为x张,那么5元纸币有(12-x)张,所以x+5(12-x)=48.2.小明准备为希望工程捐款,他现有20元,以后每月打算存10元,若不计利息,设x个月后他能捐出100元,则下列方程中能正确计算出x的是( )
A.10x+20=100 B.10x-20=100
C.20-10x=100 D.20x+10=100
【解析】选A.小明x个月后共有(10x+20)元,根据题意可列方程:10x+20=100.3.某市在端午节准备举行划龙舟大赛,预计15个队共330人参加,已知每个队一条船,每条船上人数相等,且每条船上有1人击鼓,1人掌舵,其余的人同时划桨,设每条船上划桨的有x人,那么可列出的一元一次方程为______.
【解析】划桨人数加2乘以15等于330,
即15(x+2)=330.
答案:15(x+2)=3304.七年级(1)班部分同学计划一起租车秋游,租车费人均15元;后来又有4名同学加入,总租车费不变,结果人均少花3元,设原来有x名学生,可列方程为______.
【解析】原来总租车费为15x,加入4名同学后的总租车费为(15-3)(x+4),故方程为(15-3)(x+4)=15x.
答案:(15-3)(x+4)=15x5.根据下列条件,列出方程:
(1)x的20%与10的差的一半等于-2.
(2)某数x与2的差的绝对值加上1等于2.
【解析】(1)x的20%表示为20%x;x的20%与10的差表示为20%x-
10;x的20%与10的差的一半表示为 (20%x-10),故所列方程
为 (20%x-10)=-2.
(2)某数x与2的差表示为x-2,某数x与2的差的绝对值表示为
|x-2|,某数x与2的差的绝对值加上1表示为|x-2|+1,故所列
方程为|x-2|+1=2.6.在一次植树活动中,甲班植树的株数比乙班多20%,乙班植树的株数比甲班的一半多10株.设乙班植树x株.
(1)列两个不同的含x的代数式,分别表示甲班植树的株数.
(2)根据题意列出含未知数x的方程.
(3)检验乙班、甲班植树的株数是不是分别为25株和35株.【解析】(1)根据甲班植树的株数比乙班多20%,得甲班植树的株数为(1+20%)x;根据乙班植树的株数比甲班的一半多10株,得甲班植树的株数为2(x-10).
(2)(1+20%)x=2(x-10).(3)把x=25分别代入方程的左边和右边,得
左边=(1+20%)×25=30,
右边=2×(25-10)=30.
因为左边=右边,
所以25是方程(1+20%)x=2(x-10)的解.
这就是说乙班植树的株数是25株,从上面检验过程可得甲班植树的株数是30株,而不是35株.【想一想错在哪?】已知方程(a-4)x|a|-3+2=0是关于x的一元一次方程,求a的值.
提示:未知数的系数是含有字母a的代数式,不能为0.
2.会判断一个数是否为方程的解.(重点)
3.能从简单的实际问题中找出等量关系,并列出方程.(难点)一元一次方程及有关概念
1.含有_______的等式叫做方程.
2.建立方程:把所要求的量用字母x(或y,…)表示,根据问题
中的_____关系列出方程,这一过程叫做建立方程.
3.观察方程:2x=5,y+9=0, (x-1)=3x-6,2(26-x)=22+x.未知数等量【思考】(1)观察上面的四个方程,每个方程含有未知数的个数是多少?
提示:每个方程都含有1个未知数.
(2)每个未知数的次数分别是多少?
提示:每个未知数的次数都是1.
(3)等号两边的式子是整式吗?
提示:是.
【总结】一元一次方程的定义:只含有一个未知数,并且未知数的次数是1的整式方程叫做一元一次方程.4.方程的解:能使方程左、右两边_____的未知数的___.相等值 (打“√”或“×”)
(1)4x+7是方程.( )
(2)未知数的次数是一次的方程是一元一次方程.( )
(3)设某数为x,则另一个数比它的2倍多1可列方程:x-
2=1.( )
(4)3x+1= -1是一元一次方程.( )××××知识点 1 一元一次方程的有关概念
【例1】若(m-1)x|m|+5=0是关于x的一元一次方程.
(1)求m的值,并写出这个方程.
(2)判断x=1,x=2.5,x=3是否是方程的解.【教你解题】
(1)
(2)【总结提升】
1.判断一元一次方程的三个条件
(1)只含有一个未知数.
(2)未知数的次数是1.
(3)等号两边都是整式.2.判断方程解的三个步骤
(1)代:把所给未知数的值分别代入方程等号的左右两边.
(2)算:计算等号的左右两边的值.
(3)判:若左边=右边,则是方程的解;若左边≠右边,则不是方程的解.知识点 2 列一元一次方程
【例2】(湘潭中考)湖南省2011年赴台旅游人数达7.6万人.我市某九年级一学生家长准备中考后全家3人去台湾旅游,计划花费20 000元.设每人向旅行社缴纳x元费用后,共剩
5 000元用于购物和品尝台湾美食.根据题意,列出方程为_____.【解题探究】1.此题的等量关系是什么?
提示:全家向旅行社缴纳的费用+购物和品尝台湾美食的费用=总费用.
2.题目中一家3人共向旅行社缴纳费用多少?
提示:3x元.
3.此题中的购物和品尝台湾美食的费用和总费用分别为多少元?
提示:5 000元和20 000元.
4.综上根据等量关系列出的方程是________________.3x+5 000=20 000【互动探究】此题中的等量关系还可以是什么?
提示:每人向旅行社缴纳的费用【总结提升】列方程的三个步骤
1.设:恰当地设未知数.
2.找:找出能表示应用题全部含义的一个等量关系.
3.列:根据等量关系列出方程.题组一:一元一次方程的有关概念
1.下列方程为一元一次方程的是( )
A.x+5=y+4 B.
C.x2-x=1 D.x=0
【解析】选D.选项A有两个未知数;选项B中的 不是整式;
选项C中未知数的最高次数是2,故A,B,C都不是一元一次方
程,选项D符合一元一次方程的定义.2.下列方程中,解为x=3的是( )
A.6x=2 B.3x-9=0
C. x=0 D.5x+15=0
【解析】选B.把x=3分别代入四个方程,只有方程3x-9=0左右两边相等.3.(2012·重庆中考)关于x的方程2x+a-9=0的解是x=2,则a的值为( )
A.2 B.3 C.4 D.5
【解析】选D.把x=2代入方程2x+a-9=0得2×2+a-9=0,所以a=5.4.关于x的方程xn-1+5=0是一元一次方程,求n的值.
【解析】由题意n-1=1,故n=2.5.已知y=1是方程my=y+2的解,求m2-3m+1的值.
【解析】因为y=1是方程my=y+2的解,
所以m=1+2,故m=3,
当m=3时,m2-3m+1=9-3×3+1=1.题组二:列一元一次方程
1.小悦买书需用48元钱,付款时恰好用了1元和5元的纸币共12张.设所用的1元纸币为x张,根据题意,下面所列方程正确的是( )
A.x+5(12-x)=48 B.x+5(x-12)=48
C.x+12(x-5)=48 D.5x+(12-x)=48
【解析】选A.1元纸币为x张,那么5元纸币有(12-x)张,所以x+5(12-x)=48.2.小明准备为希望工程捐款,他现有20元,以后每月打算存10元,若不计利息,设x个月后他能捐出100元,则下列方程中能正确计算出x的是( )
A.10x+20=100 B.10x-20=100
C.20-10x=100 D.20x+10=100
【解析】选A.小明x个月后共有(10x+20)元,根据题意可列方程:10x+20=100.3.某市在端午节准备举行划龙舟大赛,预计15个队共330人参加,已知每个队一条船,每条船上人数相等,且每条船上有1人击鼓,1人掌舵,其余的人同时划桨,设每条船上划桨的有x人,那么可列出的一元一次方程为______.
【解析】划桨人数加2乘以15等于330,
即15(x+2)=330.
答案:15(x+2)=3304.七年级(1)班部分同学计划一起租车秋游,租车费人均15元;后来又有4名同学加入,总租车费不变,结果人均少花3元,设原来有x名学生,可列方程为______.
【解析】原来总租车费为15x,加入4名同学后的总租车费为(15-3)(x+4),故方程为(15-3)(x+4)=15x.
答案:(15-3)(x+4)=15x5.根据下列条件,列出方程:
(1)x的20%与10的差的一半等于-2.
(2)某数x与2的差的绝对值加上1等于2.
【解析】(1)x的20%表示为20%x;x的20%与10的差表示为20%x-
10;x的20%与10的差的一半表示为 (20%x-10),故所列方程
为 (20%x-10)=-2.
(2)某数x与2的差表示为x-2,某数x与2的差的绝对值表示为
|x-2|,某数x与2的差的绝对值加上1表示为|x-2|+1,故所列
方程为|x-2|+1=2.6.在一次植树活动中,甲班植树的株数比乙班多20%,乙班植树的株数比甲班的一半多10株.设乙班植树x株.
(1)列两个不同的含x的代数式,分别表示甲班植树的株数.
(2)根据题意列出含未知数x的方程.
(3)检验乙班、甲班植树的株数是不是分别为25株和35株.【解析】(1)根据甲班植树的株数比乙班多20%,得甲班植树的株数为(1+20%)x;根据乙班植树的株数比甲班的一半多10株,得甲班植树的株数为2(x-10).
(2)(1+20%)x=2(x-10).(3)把x=25分别代入方程的左边和右边,得
左边=(1+20%)×25=30,
右边=2×(25-10)=30.
因为左边=右边,
所以25是方程(1+20%)x=2(x-10)的解.
这就是说乙班植树的株数是25株,从上面检验过程可得甲班植树的株数是30株,而不是35株.【想一想错在哪?】已知方程(a-4)x|a|-3+2=0是关于x的一元一次方程,求a的值.
提示:未知数的系数是含有字母a的代数式,不能为0.
同课章节目录
