湘教版数学八年级上册 课件:2.1《三角形的有关概念及三边关系》(共17张PPT)
文档属性
| 名称 | 湘教版数学八年级上册 课件:2.1《三角形的有关概念及三边关系》(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-22 18:04:47 | ||
图片预览




文档简介
课件17张PPT。三角形2.1 观察下图,找一找图中的三角形,并把它们勾画出来. 阅读课本42至43页思考下列问题:1.什么样的图形叫做三角形?如何表示一个三角形?什么是三角形的顶点,边,内角?
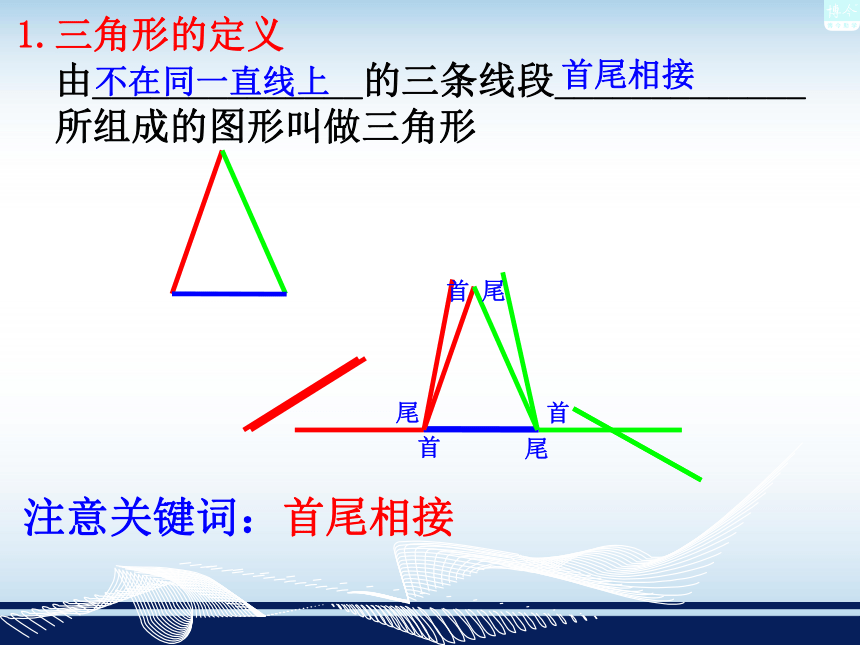
2.在三角形中,角的对边是指什么?边的对角是指什么?3.什么样的三角形是等腰三角形或等边三角形?等腰三角形的腰、顶角、底角分别指什么?4.在三角形中,三条边要满足什么关系? 请同学们完成学案"预习"部分不在同一直线上首尾相接首首首尾尾尾1.三角形的定义
由______________的三条线段_____________
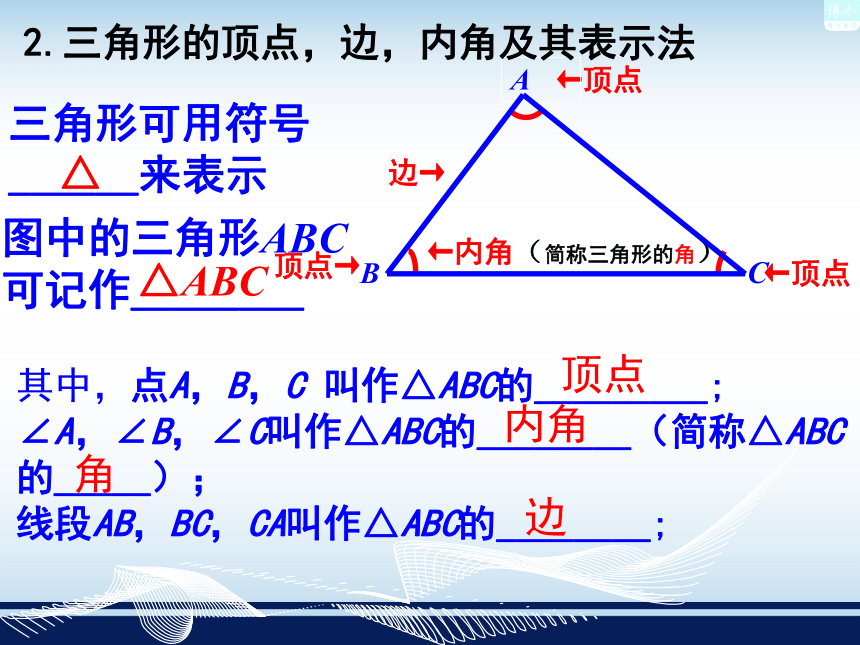
所组成的图形叫做三角形注意关键词:首尾相接←顶点←内角(简称三角形的角)边→2.三角形的顶点,边,内角及其表示法三角形可用符号
______来表示图中的三角形ABC
可记作________顶点→←顶点其中,点A,B,C 叫作△ABC的_________;
∠A,∠B,∠C叫作△ABC的________(简称△ABC的_____);
线段AB,BC,CA叫作△ABC的________;
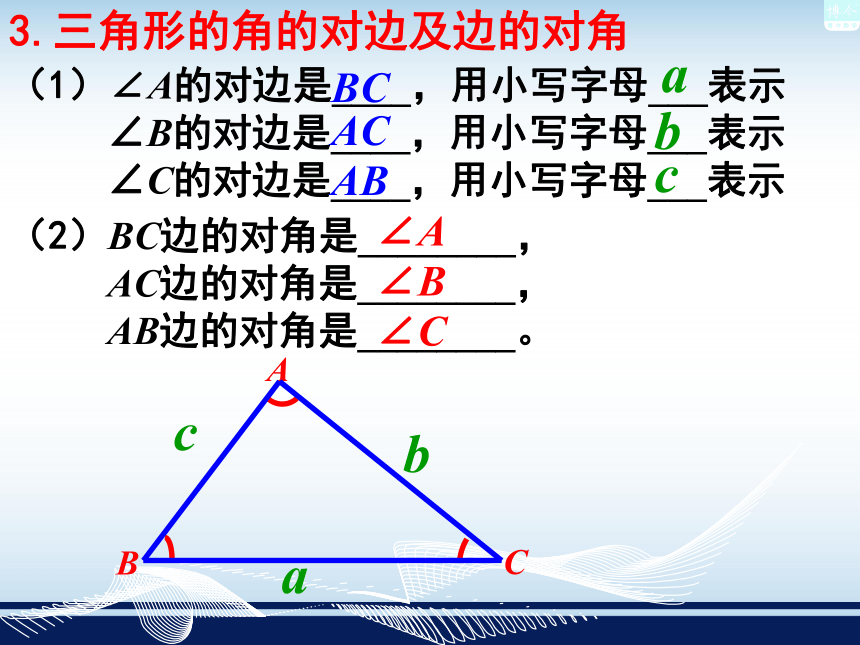
△△ABC顶点内角角边 (1)∠A的对边是____,用小写字母___表示
∠B的对边是____,用小写字母___表示
∠C的对边是____,用小写字母___表示a3.三角形的角的对边及边的对角(2)BC边的对角是________,
AC边的对角是________,
AB边的对角是________。BCaACbbABcc∠A∠B∠C底边底角底角4.等腰三角形与等边三角形(1)______________的三角形叫作等腰三角形.有两条边相等如图△ABC中,AB =AC,则△ABC是______三角形等腰(2)___________的三角形叫作等边(正)三角形.三边都相等如图△ABC中,AB =AC=BC,则△ABC是____三角形等边思考交流:
等腰三角形与
等边三角形有何关系?等边三角形是特殊的等腰三角形——腰和底边相等的等腰三角形. 在一个三角形中,任意两边之和与第三边的长度之间有怎样的大小关系?为什么?三角形的三边之间的关系为____________________________.三角形的任意两边之和大于第三边 在△ABC中,BC是连接B,C两点的一条线段,由基本事实“两点之间线段最短”可得 AB + AC > BC.同理可得AB + BC > AC,AC + BC > AB .三角形的任意两边之和大于第三边.
三角形的任意两边之差小于第三边.构成三角形的条件AB > BC-AC
AC > BC-ABBC > AC-AB只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.1.下列长度的各组线段能否组成一个三角形,并说明理由?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm练一练三角形的任意两边之和大于第三边.两短边之和大于长边.
其实质就是:3.一个等腰三角形的一边长9cm,另一边长4cm,则它的周长是多少?为什么?
提示:既然是等腰三角形,那么另一边的长要么是4cm, 要么是9cm.
如果是4cm,那么4 ﹢ 4﹤9cm,这样不满足三角形的三边关系,所以另一边的长只能是9cm,周长就应该是9﹢9﹢4=22cm.
2.一个三角形的两边长分别是2cm、5cm,则第三边长X的取值范围是多少? 分析: X应满足大于5﹣2﹦3cm,小于5 ﹢ 2 ﹦7cm,所以3﹤X﹤7. 举
例例1 如图,D是△ABC的边AC上一点,AD=BD,
试判断AC与BC的大小.解 在△BDC 中,有 BD+DC >BC(三角形的任意两边之和大于第三边).又 AD = BD,则 BD+DC = AD+DC = AC,所以 AC >BC.1.(1)如图,图中有几个三角形?把它们分别
表示出来.答:五个三角形.(2)如图,在△DBC 中,写出∠D 的对边,
BD 边的对角.答:∠D的对边是BC,
BD边的对角是∠BCD.2. 三根长分别为2cm,5cm,6cm的小木棒能
首尾相接构成一个三角形吗?答:能.谢谢大家!学习当激流勇进,
人生当自强不息。
2.在三角形中,角的对边是指什么?边的对角是指什么?3.什么样的三角形是等腰三角形或等边三角形?等腰三角形的腰、顶角、底角分别指什么?4.在三角形中,三条边要满足什么关系? 请同学们完成学案"预习"部分不在同一直线上首尾相接首首首尾尾尾1.三角形的定义
由______________的三条线段_____________
所组成的图形叫做三角形注意关键词:首尾相接←顶点←内角(简称三角形的角)边→2.三角形的顶点,边,内角及其表示法三角形可用符号
______来表示图中的三角形ABC
可记作________顶点→←顶点其中,点A,B,C 叫作△ABC的_________;
∠A,∠B,∠C叫作△ABC的________(简称△ABC的_____);
线段AB,BC,CA叫作△ABC的________;
△△ABC顶点内角角边 (1)∠A的对边是____,用小写字母___表示
∠B的对边是____,用小写字母___表示
∠C的对边是____,用小写字母___表示a3.三角形的角的对边及边的对角(2)BC边的对角是________,
AC边的对角是________,
AB边的对角是________。BCaACbbABcc∠A∠B∠C底边底角底角4.等腰三角形与等边三角形(1)______________的三角形叫作等腰三角形.有两条边相等如图△ABC中,AB =AC,则△ABC是______三角形等腰(2)___________的三角形叫作等边(正)三角形.三边都相等如图△ABC中,AB =AC=BC,则△ABC是____三角形等边思考交流:
等腰三角形与
等边三角形有何关系?等边三角形是特殊的等腰三角形——腰和底边相等的等腰三角形. 在一个三角形中,任意两边之和与第三边的长度之间有怎样的大小关系?为什么?三角形的三边之间的关系为____________________________.三角形的任意两边之和大于第三边 在△ABC中,BC是连接B,C两点的一条线段,由基本事实“两点之间线段最短”可得 AB + AC > BC.同理可得AB + BC > AC,AC + BC > AB .三角形的任意两边之和大于第三边.
三角形的任意两边之差小于第三边.构成三角形的条件AB > BC-AC
AC > BC-ABBC > AC-AB只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.1.下列长度的各组线段能否组成一个三角形,并说明理由?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm练一练三角形的任意两边之和大于第三边.两短边之和大于长边.
其实质就是:3.一个等腰三角形的一边长9cm,另一边长4cm,则它的周长是多少?为什么?
提示:既然是等腰三角形,那么另一边的长要么是4cm, 要么是9cm.
如果是4cm,那么4 ﹢ 4﹤9cm,这样不满足三角形的三边关系,所以另一边的长只能是9cm,周长就应该是9﹢9﹢4=22cm.
2.一个三角形的两边长分别是2cm、5cm,则第三边长X的取值范围是多少? 分析: X应满足大于5﹣2﹦3cm,小于5 ﹢ 2 ﹦7cm,所以3﹤X﹤7. 举
例例1 如图,D是△ABC的边AC上一点,AD=BD,
试判断AC与BC的大小.解 在△BDC 中,有 BD+DC >BC(三角形的任意两边之和大于第三边).又 AD = BD,则 BD+DC = AD+DC = AC,所以 AC >BC.1.(1)如图,图中有几个三角形?把它们分别
表示出来.答:五个三角形.(2)如图,在△DBC 中,写出∠D 的对边,
BD 边的对角.答:∠D的对边是BC,
BD边的对角是∠BCD.2. 三根长分别为2cm,5cm,6cm的小木棒能
首尾相接构成一个三角形吗?答:能.谢谢大家!学习当激流勇进,
人生当自强不息。
同课章节目录
