小升初分班考冲刺特训卷-数学六年级下册人教版(含解析)
文档属性
| 名称 | 小升初分班考冲刺特训卷-数学六年级下册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 517.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-06 15:10:10 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初分班考冲刺特训卷-数学六年级下册人教版
一、选择题
1.用三根同样长的绳子,分别围成一个长方形、正方形和圆形,面积最大的是( )。
A.长方形 B.正方形 C.圆形 D.平行四边形
2.袋子里有红色、黑色、白色小球各10个,要求闭着眼睛保证一次摸出3个同色的小球,至少要摸出( )个小球。
A.3 B.4 C.7 D.21
3.与24÷结果相等的式子是( )。
A.24÷5×3 B.24÷3×5 C.24÷3÷5 D.24×3×5
4.一个长方体的棱长总和是60厘米,长、宽、高的比是5∶4∶6。这个长方体的高是( )厘米。
A.4 B.6 C.24 D.20
5.甲数的倒数是,乙数的倒数是4,甲、乙两数和的25%是( )。
A.1.75 B. C. D.
6.一种商品,降价20元后,卖180元,比原价降低了( )。
A.10% B.12.5% C.约11.1% D.90%
二、填空题
7.乐乐全家四口人到一处名胜古迹旅游,由其中一人轮换给其他人拍照,如果单人各照一张,每两人合影一张,每三人合影一张,则他们一共要拍( )张照片。
8.有一箱苹果,甲班分,每人3个还剩10个;乙班分,每人4个还剩11个;丙班分,每人5个还剩12个;那么这箱苹果至少有( )个。
9.小红和小明参加一个联欢会,在联欢会中,小红看到不戴眼镜的同学是戴眼镜同学的2倍,小明看到戴眼镜的同学是不戴眼镜同学的,参加联欢会的同学共有( )名。
10.在直角三角形中,一个锐角是45°,另一个锐角是( )°,这也是一个( )三角形。
11.如图,平行四边形的面积是20cm2,图中甲、乙、丙三个三角形的面积比是( ),涂色部分的面积是( )cm2。
12.一幅地图中某两地的图上距离5厘米表示实际距离15千米,这幅图的比例尺是( )。
13.有2元和5元的人民币共30张,合计75元,则面值2元的人民币有( )张,面值5元的人民币有( )张。
14.一个正方体木块的棱长是6厘米,把它削成一个最大的圆柱体,圆柱体的体积是( )立方厘米,再把这个圆柱体削成一个最大的圆锥体,圆锥体的体积约是( )立方厘米。
三、判断题
15.42∶4和10.5∶1能组成比例。( )
16.小数0.074中的数字“7”表示7个百分之一。( )
17.一批零件里100件正品,4件次品,正品率为100%。( )
18.10℃比﹣7℃高3℃。( )
19.在一条线段上共有8个点,则这8个点可以构成28条线段。( )
四、计算题
20.直接写出得数。
427+336= 83-1.75= 125×0.08= 4.5÷0.05=
-= 10.1÷1%= 2.57×0.4÷2.57×0.4= 1-1÷8=
21.用递等式计算,能简便计算的要简便计算。
(1)1.05×(3.8-0.8)÷6.3 (2)44÷[(-)×2] (3)8.3×9.8+2×0.83
22.解方程或比例。
x-x= 0.45∶x=0.2∶8 5x+1.25=1.75
23.求阴影部分的面积。(单位:cm,取3。)
五、解答题
24.某品牌饮料搞促销活动,在A商场每满100元减20元,在B商场打八五折,在C商场买10送2,三个商场的标价都是每瓶4.5元,要买60瓶这种饮料。在A、B、C三个商场买,哪个商场更省钱?
25.一辆运货汽车从甲地到乙地,平均每小时行72千米,5小时到达。回来时空车原路返回平均每小时行80千米,需要几个小时?(用比例解)
26.一堆煤堆成圆锥形,测得底面周长是18.84米,高是3米,已知每立方米的煤约重1.4吨,这堆煤约重多少吨?
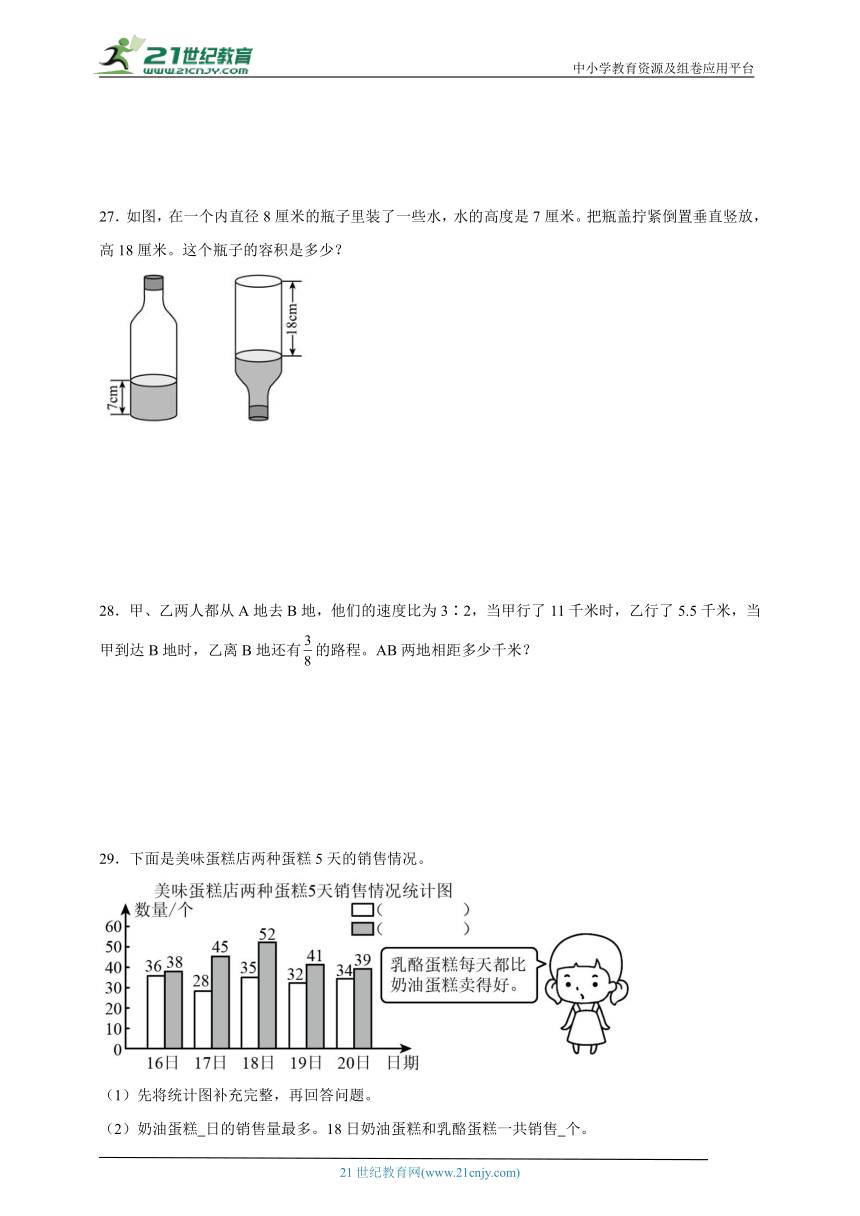
27.如图,在一个内直径8厘米的瓶子里装了一些水,水的高度是7厘米。把瓶盖拧紧倒置垂直竖放,高18厘米。这个瓶子的容积是多少?
28.甲、乙两人都从A地去B地,他们的速度比为3∶2,当甲行了11千米时,乙行了5.5千米,当甲到达B地时,乙离B地还有的路程。AB两地相距多少千米?
29.下面是美味蛋糕店两种蛋糕5天的销售情况。
(1)先将统计图补充完整,再回答问题。
(2)奶油蛋糕 日的销售量最多。18日奶油蛋糕和乳酪蛋糕一共销售 个。
(3)这5天乳酪蛋糕平均每日销售 个。
(4)19日销售的奶油蛋糕比16日的奶油蛋糕减少了百分之几?
参考答案:
1.C
【分析】根据题意,四个图形的周长相同,故可以设出其周长,从而可求出四个图形的面积,再进行比较。
【详解】假设绳子的长度是4,长方形、正方形和圆的周长都是4,
正方形的面积:4÷4=1
1×1=1
长方形的面积:
4÷2=2
假设长是1.6,宽是0.4,
1.6×0.4=0.64
假设平行四边形的底边长是1.6,长方形和平行四边形两者底边相等的情况下,长方形的高大于平行四边形的高,所以平行四边形的面积小于长方形的面积;
圆的面积是:
=3.14×
=2×
=
=
因此圆的面积最大。
故答案为:C
【点睛】本题运用长方形、正方形、圆、平行四边形的面积公式进行解答即可。以后记住周长相同的所有图形中,圆的面积最大。
2.C
【分析】考虑最倒霉的情况,红色、黑色、白色各摸出2个,再摸一个,无论什么颜色,都能保证摸出3个同色的小球,据此分析。
【详解】3×2+1
=6+1
=7(个)
至少要摸出7个小球。
故答案为:C
【点睛】关键是构造物体和抽屉,也就是找到代表物体和抽屉的量,然后依据抽屉原则进行计算。
3.B
【分析】除以一个数等于乘这个数的倒数,再根据分数的分子相当于被除数,分母相当于除数,改写成整数乘除法的形式即可。
【详解】24÷
=24×
=24÷3×5→与选项B相同
=40
与24÷结果相等的式子是24÷3×5。
故答案为:B
【点睛】关键是掌握分数除法的计算方法。
4.B
【分析】根据长方体的棱长总和= (a+b+h)×4,首先用棱长总和除以4求出长、宽高的和,已知长、宽、高的比是5∶4∶6,利用按比例分配的方法,求出长方体的高是多少厘米即可。
【详解】60÷4=15(厘米)
15×
=15×
=6(厘米)
即这个长方体的高是6厘米。
故答案为:B
【点睛】此题主要考查长方体的棱长总和公式的灵活运用,按比例分配的方法及应用,关键是熟记公式。
5.D
【分析】交换真分数分子和分母的位置,即可得到它的倒数,整数的倒数是这个整数分之一,据此确定甲数和乙数,求和,再根据求一个数的百分之几是多少,用乘法计算即可。
【详解】(+)×25%
=×
=
甲数的倒数是,乙数的倒数是4,甲、乙两数和的25%是。
故答案为:D
【点睛】关键是理解倒数的含义,掌握求一个数的百分之几是多少的方法。
6.A
【分析】降价钱数+现价=原价,降价钱数÷原价=比原价降低了百分之几,据此列式计算。
【详解】20÷(20+180)
=20÷200
=0.1
=10%
比原价降低了10%。
故答案为:A
【点睛】此类问题一般用表示单位“1”的量作除数。
7.14
【分析】设四人为a,b,c,d,单人照有4种:a,b,c,d;两人合影有6种:ab,ac,ad,bc,bd,cd;三人合影有4种:abc,abd,acd,bcd;所以一共有(4+6+4)种。
【详解】4+6+4=14(张)
他们一共要拍14张照片。
8.67
【分析】每人3个还剩10个,10-3=7,也就是这批苹果的数量是3的倍数还多7;每人4个还剩11个,11-4=7,也就是这批苹果的数量是4的倍数还多7;每人5个还剩12个,12-5=7,所以这批数量是5的倍数多7。这批苹果的数量是3、4、5的公倍数多7;因为3、4、5两两互质,则用3×4×5即可求出这三个数的最小公倍数,再加上7即可求出这批苹果的数量最少是多少。
【详解】10-3=7
11-4=7
12-5=7
3×4×5=60
60+7=67(个)
这箱苹果至少有67个。
【点睛】本题主要考查了最小公倍数的灵活应用,找到相同的余数是解答本题的关键。
9.16
【分析】小红和小明看到的全班的人数总和是总共人数-1且是不变的,也就是他们看到的总人数。以他们看到的总人数为单位“1”,小红看到不戴眼镜的同学是戴眼镜同学的2倍,戴眼镜的人数是1份,那么不带眼镜的人数就是2份,戴眼镜占他们看到的总人数的。小明看到戴眼镜的同学是不戴眼镜同学的,则戴眼镜的同学是2份,不戴眼镜的同学是3份,戴眼镜占他们看到的总人数的。如果小红和小明两个人都戴眼镜或都不戴眼镜,看到的比例分数应该是一样,但是小明看到的比小红比例多,则小明不戴眼镜,小红戴眼镜,也就是小明看到的戴眼镜的比小红看到的戴眼镜的多1人,多的1人正好是他们看到的总人数的。那么看到的人数为15人。注意最后还要加上1(也就是自己)。
【详解】
=
1÷=15(名)
15+1=16(名)
参加联欢会的同学共有16名。
10. 45 等腰直角/等腰
【分析】由题意可知,已知是直角三角形,一个锐角是45°,根据三角形的内角和是180°,即可计算出另一个锐角的度数,然后比较两个锐角的大小,再根据等腰三角形的性质判断即可。
【详解】180°-90°-45°
=90°-45°
=45°
所以另一个锐角是45°,两个锐角相等,这也是一个等腰直角三角形。
11. 5∶2∶3 4
【分析】观察图形可知,平行四边形底是(2+3)cm,根据平行四边形面积公式:面积=底×高;高=面积÷底,代入数据,求出平行四边形的高;甲、乙、丙三个三角形的高等于平行四边形的高,甲的底等于平行四边形的底,根据三角形面积公式:面积=底×高÷2,代入数据,求出甲、乙、丙三个三角形面积,再根据比的意义,用甲的面积∶乙的面积∶丙的面积,求出三个三角形面积比;涂色部分等于乙三角形面积,据此解答。
【详解】高:20÷(2+3)
=20÷5
=4(cm)
甲:(2+3)×4÷2
=5×4÷2
=20÷2
=10(cm2)
乙:2×4÷2
=8÷2
=4(cm2)
丙:3×4÷2
=12÷2
=6(cm2)
10∶4∶6
=(10÷2)∶(4÷2)∶(6÷2)
=5∶2∶3
涂色面积是4cm2。
如图,平行四边形的面积是20cm2,图中甲、乙、丙三个三角形的面积比是5∶2∶3,涂色部分的面积是4cm2。
12.1∶300000/
【分析】先统一单位,再根据比例尺=图上距离∶实际距离,写出这幅图的比例尺即可。
【详解】15千米=1500000厘米
5厘米∶1500000厘米
=(5÷5)∶(1500000÷5)
=1∶300000
这幅图的比例尺是1∶300000。
【点睛】本题主要考查了比例尺的意义,注意单位要统一。
13. 25 5
【分析】设2元的人民币有x张,则5元的人民币(30-x)张,又知“合计人民币75元”,可得等量关系式:面值2元的人民币×张数+面值5元的人民币×张数=75,据此等量列方程解答。
【详解】解:设2元的人民币有x张,则5元的人民币(30-x)张,由题意得:
2x+5(30-x)=75
2x+150-5x=75
2x+150-5x-2x=75-2x
150-5x=75-2x
150-5x+5x=75-2x+5x
150=75+3x
150-75=75+3x-75
3x=75
3x÷3=75÷3
x=25
30-x
=30-25
=5(张)
2元的25张,5元的5张。
【点睛】鸡兔同笼问题用方程解答容易想,根据其中一个等量关系表示两个未知量,另一个等量关系列方程。
14. 169.56 56.52
【分析】把正方体削成一个最大的圆柱,则这个圆柱的底面直径是6厘米,高是6厘米,根据圆柱的体积公式:V=πr2h,用3.14×(6÷2)2×6即可求出圆柱的体积;再把圆柱削成一个最大的圆锥,则这个圆锥的底面直径是6厘米,高是6厘米,根据圆锥的体积公式:V=πr2h,用×3.14×(6÷2)2×6即可求出圆锥的体积。
【详解】3.14×(6÷2)2×6
=3.14×32×6
=3.14×9×6
=169.56(立方厘米)
169.5656.52(立方厘米)
圆柱的体积是169.56立方厘米,圆锥的体积是56.52立方厘米。
【点睛】本题主要考查了圆柱体积公式和圆锥体积公式的应用。
15.√
【分析】可以用求比值的方法:两个比的比值相等,就能组成比例,比值不相等,就不能组成比例;也可以根据比例的性质:两外项的积等于两内项的积,据此逐项分析再选择。
【详解】因42×1=42,4×10.5=42,所以42∶4和10.5∶1能组成比例。故原题说法正确。
故答案为:√
【点睛】本题主要考查了比的意义及基本性质的灵活运用。
16.√
【分析】小数的整数部分从右边起,分别是个位、十位、百位……小数部分从左边起,分别是十分位、百分位、千分位……十分位的计数单位是十分之一,百分位的计数单位是百分之一,千分位的计数单位是千分之一……据此解答即可。
【详解】0.074中的“7”在百分位上,表示7个百分之一。原题说法正确。
故答案为:√
【点睛】此题考查小数的数位和计数单位,要熟练掌握。
17.×
【分析】根据题意,正品率=正品数量÷总数量×100%,由此代入数据判断。
【详解】100÷(100+4)×100%
=100÷104×100%
≈96.2%
96.2%<100%
一批零件里100件正品,4件次品,正品率约96.2%,为原题说法错误;
故答案为:×
【点睛】此题属于百分率问题,都是用一部分数量(或全部数量)除以全部数量乘100%。
18.×
【分析】用10℃和0℃相差10℃,用﹣7℃和0℃相差7℃,用10℃+7℃即可求出这两个温度相差多少。
【详解】10℃+7℃=17℃
所以10℃比﹣7°C高17℃。
所以题干说法是错误的。
故答案为:×
【点睛】熟练掌握正、负数的运算方法,是解答此题的关键。
19.√
【分析】每个点都可以和另外7个点连成7条线段,共能连成8×7=56(条)线段,由于每条线段重复计算了一次,所以共能连成56÷2=28(条)线段;据此解答即可。
【详解】8×(8-1)÷2
=8×7÷2
=56÷2
=28(条)
即这8个点可以构成28条线段,所以原题说法正确。
故答案为:√
【点睛】本题考查了线段的计数问题,实质是握手问题,可以直接根据计算公式解答。
20.763;81.25;10;90
;1010;0.16;
【详解】略
21.(1)0.5;(2)36;(3)83
【分析】(1)先算小括号里面的减法,再按照从左向右的顺序进行计算;
(2)先算小括号里面的减法,再算中括号里面的乘法,最后算括号外面的除法;
(3)先根据积不变性质,将算式变为8.3×9.8+0.2×8.3,然后根据乘法分配律,将算式变为8.3×(9.8+0.2)进行计算。
【详解】(1)1.05×(3.8-0.8)÷6.3
=1.05×3÷6.3
=3.15÷6.3
=0.5
(2)44÷[(-)×2]
=44÷[×2]
=44÷
=44×
=36
(3)8.3×9.8+2×0.83
=8.3×9.8+0.2×8.3
=8.3×(9.8+0.2)
=8.8×10
=83
22.x=;x=18;x=0.5
【分析】(1)先化简,然后再根据等式的性质,方程两边同时除以求解;
(2)把比例化成一般方程0.2x=0.45×8,再根据等式的性质,方程两边同时除以0.2即可得到原比例的解;
(3)再根据等式的性质,方程两边同时减去1.25,然后再同时除以5求解。
【详解】x-x=
解:x=
x÷=÷
x=×6
x=
0.45∶x=0.2∶8
解:0.2x=0.45×8
0.2x=3.6
0.2x÷0.2=3.6÷0.2
x=18
5x+1.25=3.75
解:5x+1.25-1.25=3.75-1.25
5x=2.5
5x÷5=2.5÷5
x=0.5
23.13.5平方厘米
【分析】根据图示,先求出三角形的底(也就是半圆的直径),然后用半圆的面积减去三角形的面积即可;三角形的底=三角形的面积×2÷高,先利用两条直角边求出三角形的面积,再代入公式求出三角形的底边;圆的面积=πr 。
【详解】三角形的底(也就是半圆的直径)是:
8×6÷2×2÷4.8
=48÷4.8
=10(厘米)
阴影部分的面积:
3×(10÷2)2÷2-8×6÷2
=3×25÷2-24
=37.5-24
=13.5(平方厘米)
阴影部分的面积是13.5平方厘米。
24.C商场
【分析】A商场:每满100元返20元,根据单价×数量=总价,代入求出60瓶这种饮料的原价,计算原价里面有多少个100元,就减多少个20元,用原价减去优惠的价格,即可求出A商场优惠后的价格。
B商场:八五折=85%,先根据单价×数量=总价,代入求出60瓶这种饮料的原价,乘折扣85%,即可求出B商场优惠后的价格;
C商场:买10送2,先计算60个里面有多少个(10+2),即送多少个2,求出购买的实际数量,再乘饮料的单价,即可求出C商场优惠后的价格;比较三家商场优惠后价格即可得解。
【详解】A商场:4.5×60÷100≈2(个)
4.5×60-2×20
=270-40
=230(元)
B商场:
4.5×60×85%
=270×85%
=229.5(元)
C商场:
60÷(10+2)
=60÷12
=5(个)
60-2×5
=60-10
=50(瓶)
4.5×50=225(元)
225<229.5<230
答:C商场更省钱。
【点睛】最优化问题常用比较法进行解答,分别计算出三种方案优惠后的价格,再进行比较。
25.4.5个小时
【分析】由题意可知,去时和返回的路程不变,根据速度×时间=路程,则速度和时间成反比例,据此列比例解答即可。
【详解】解:设x小时能够返回原地。
80x=72×5
80x=360
80x÷80=360÷80
x=4.5
答:需要4.5个小时。
【点睛】本题考查用比例解决实际问题,明确速度和时间成反比例是解题的关键。
26.39.564吨
【分析】根据圆的周长公式:C=2πr,据此求出圆锥底面的半径,再根据圆锥的体积公式:V=πr2h,据此求出这堆煤的体积,再乘1.4即可求解。
【详解】18.84÷3.14÷2
=6÷2
=3(米),
3.14×32×3×
=3.14×9×(3×)
=28.26×1
=28.26(立方米)
28.26×1.4=39.564(吨)
答:这堆煤约重39.564吨。
【点睛】本题考查圆锥的体积,熟记公式是解题的关键。
27.1256毫升
【分析】瓶子的底面直径和正放时液面的高度已知,根据圆柱的体积公式:V=,则可以求出瓶内液体的体积,同样的方法,可以求出倒放时空余部分的体积,瓶子的容积=饮料的体积+倒放时空余部分的体积。据此解答。
【详解】8÷2=4(厘米)
3.14×42×7+3.14×42×18
=3.14×16×7+3.14×16×18
=351.68+904.32
=1256(立方厘米)
=1256(毫升)
答:这个瓶子的容积是1256毫升。
【点睛】此题解答关键是利用体积不变的特性,把不规则图形转化为规则图形来计算。
28.44千米
【分析】根据题意,甲、乙两人的速度比为3∶2,当两人用的时间相同时,甲、乙两人的路程比等于速度比3∶2,即甲走的路程是乙路程的;先求出乙行了5.5千米的时间,甲行了5.5×=8.25千米,而实际甲行了11千米,说明甲比乙先行11-8.25=2.75千米;
又已知当甲到达B地时,乙离B地还有的路程,把全程看作单位“1”,则乙行了全程的(1-),而甲行的路程是乙的,所以甲行了全程的(1-)×=;那么甲先行的路程占全程的(1-),单位“1”未知,用甲先行的路程除以(1-),即可求出AB两地的距离。
【详解】当乙行了5.5千米时,甲只能行:
5.5×=8.25(千米)
所以甲比乙先行:11-8.25=2.75(千米)
当乙离B地还有的路程时,甲行了全程的:
(1-)×
=×
=
全程:
2.75÷(1-)
=2.75÷
=2.75×16
=44(千米)
答:AB两地相距44千米。
【点睛】本题考查分数除法的实际应用,先把比转化成分数,明确时间相同时,两人的路程比等于他们的速度比;分析出甲先行的路程占全程的几分之几,然后根据分数除法的意义解答。
29.(1)见解答
(2)16,87
(3)43
(4)11.1%
【分析】(1)阴影条形每天都比空白条形高,所以阴影条形表示乳酪蛋糕,空白条形表示奶油蛋糕。
(2)奶油蛋糕16日的销售量最多。18日奶油蛋糕和乳酪蛋糕一共销售多少个用加法计算。
(3)五天的乳酪蛋糕的和除以天数就得平均数。
(4)用16日的奶油蛋糕数量减去19日的奶油蛋糕数量再除以16日的奶油蛋糕数量。
【详解】(1)如图:
(2)35+52=87(个)
奶油蛋糕16日的销售量最多。18日奶油蛋糕和乳酪蛋糕一共销售87个。
(3)(38+45+52+41+39)÷5
=215÷5
=43(个)
这5天乳酪蛋糕平均每日销售43个。
(4)(36-32)÷36
=4÷36
≈11.1%
答:19日销售的奶油蛋糕比16日的奶油蛋糕减少了11.1%。
【点睛】本题考查了学生对统计图意义的掌握及从统计图中获取信息的意识。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初分班考冲刺特训卷-数学六年级下册人教版
一、选择题
1.用三根同样长的绳子,分别围成一个长方形、正方形和圆形,面积最大的是( )。
A.长方形 B.正方形 C.圆形 D.平行四边形
2.袋子里有红色、黑色、白色小球各10个,要求闭着眼睛保证一次摸出3个同色的小球,至少要摸出( )个小球。
A.3 B.4 C.7 D.21
3.与24÷结果相等的式子是( )。
A.24÷5×3 B.24÷3×5 C.24÷3÷5 D.24×3×5
4.一个长方体的棱长总和是60厘米,长、宽、高的比是5∶4∶6。这个长方体的高是( )厘米。
A.4 B.6 C.24 D.20
5.甲数的倒数是,乙数的倒数是4,甲、乙两数和的25%是( )。
A.1.75 B. C. D.
6.一种商品,降价20元后,卖180元,比原价降低了( )。
A.10% B.12.5% C.约11.1% D.90%
二、填空题
7.乐乐全家四口人到一处名胜古迹旅游,由其中一人轮换给其他人拍照,如果单人各照一张,每两人合影一张,每三人合影一张,则他们一共要拍( )张照片。
8.有一箱苹果,甲班分,每人3个还剩10个;乙班分,每人4个还剩11个;丙班分,每人5个还剩12个;那么这箱苹果至少有( )个。
9.小红和小明参加一个联欢会,在联欢会中,小红看到不戴眼镜的同学是戴眼镜同学的2倍,小明看到戴眼镜的同学是不戴眼镜同学的,参加联欢会的同学共有( )名。
10.在直角三角形中,一个锐角是45°,另一个锐角是( )°,这也是一个( )三角形。
11.如图,平行四边形的面积是20cm2,图中甲、乙、丙三个三角形的面积比是( ),涂色部分的面积是( )cm2。
12.一幅地图中某两地的图上距离5厘米表示实际距离15千米,这幅图的比例尺是( )。
13.有2元和5元的人民币共30张,合计75元,则面值2元的人民币有( )张,面值5元的人民币有( )张。
14.一个正方体木块的棱长是6厘米,把它削成一个最大的圆柱体,圆柱体的体积是( )立方厘米,再把这个圆柱体削成一个最大的圆锥体,圆锥体的体积约是( )立方厘米。
三、判断题
15.42∶4和10.5∶1能组成比例。( )
16.小数0.074中的数字“7”表示7个百分之一。( )
17.一批零件里100件正品,4件次品,正品率为100%。( )
18.10℃比﹣7℃高3℃。( )
19.在一条线段上共有8个点,则这8个点可以构成28条线段。( )
四、计算题
20.直接写出得数。
427+336= 83-1.75= 125×0.08= 4.5÷0.05=
-= 10.1÷1%= 2.57×0.4÷2.57×0.4= 1-1÷8=
21.用递等式计算,能简便计算的要简便计算。
(1)1.05×(3.8-0.8)÷6.3 (2)44÷[(-)×2] (3)8.3×9.8+2×0.83
22.解方程或比例。
x-x= 0.45∶x=0.2∶8 5x+1.25=1.75
23.求阴影部分的面积。(单位:cm,取3。)
五、解答题
24.某品牌饮料搞促销活动,在A商场每满100元减20元,在B商场打八五折,在C商场买10送2,三个商场的标价都是每瓶4.5元,要买60瓶这种饮料。在A、B、C三个商场买,哪个商场更省钱?
25.一辆运货汽车从甲地到乙地,平均每小时行72千米,5小时到达。回来时空车原路返回平均每小时行80千米,需要几个小时?(用比例解)
26.一堆煤堆成圆锥形,测得底面周长是18.84米,高是3米,已知每立方米的煤约重1.4吨,这堆煤约重多少吨?
27.如图,在一个内直径8厘米的瓶子里装了一些水,水的高度是7厘米。把瓶盖拧紧倒置垂直竖放,高18厘米。这个瓶子的容积是多少?
28.甲、乙两人都从A地去B地,他们的速度比为3∶2,当甲行了11千米时,乙行了5.5千米,当甲到达B地时,乙离B地还有的路程。AB两地相距多少千米?
29.下面是美味蛋糕店两种蛋糕5天的销售情况。
(1)先将统计图补充完整,再回答问题。
(2)奶油蛋糕 日的销售量最多。18日奶油蛋糕和乳酪蛋糕一共销售 个。
(3)这5天乳酪蛋糕平均每日销售 个。
(4)19日销售的奶油蛋糕比16日的奶油蛋糕减少了百分之几?
参考答案:
1.C
【分析】根据题意,四个图形的周长相同,故可以设出其周长,从而可求出四个图形的面积,再进行比较。
【详解】假设绳子的长度是4,长方形、正方形和圆的周长都是4,
正方形的面积:4÷4=1
1×1=1
长方形的面积:
4÷2=2
假设长是1.6,宽是0.4,
1.6×0.4=0.64
假设平行四边形的底边长是1.6,长方形和平行四边形两者底边相等的情况下,长方形的高大于平行四边形的高,所以平行四边形的面积小于长方形的面积;
圆的面积是:
=3.14×
=2×
=
=
因此圆的面积最大。
故答案为:C
【点睛】本题运用长方形、正方形、圆、平行四边形的面积公式进行解答即可。以后记住周长相同的所有图形中,圆的面积最大。
2.C
【分析】考虑最倒霉的情况,红色、黑色、白色各摸出2个,再摸一个,无论什么颜色,都能保证摸出3个同色的小球,据此分析。
【详解】3×2+1
=6+1
=7(个)
至少要摸出7个小球。
故答案为:C
【点睛】关键是构造物体和抽屉,也就是找到代表物体和抽屉的量,然后依据抽屉原则进行计算。
3.B
【分析】除以一个数等于乘这个数的倒数,再根据分数的分子相当于被除数,分母相当于除数,改写成整数乘除法的形式即可。
【详解】24÷
=24×
=24÷3×5→与选项B相同
=40
与24÷结果相等的式子是24÷3×5。
故答案为:B
【点睛】关键是掌握分数除法的计算方法。
4.B
【分析】根据长方体的棱长总和= (a+b+h)×4,首先用棱长总和除以4求出长、宽高的和,已知长、宽、高的比是5∶4∶6,利用按比例分配的方法,求出长方体的高是多少厘米即可。
【详解】60÷4=15(厘米)
15×
=15×
=6(厘米)
即这个长方体的高是6厘米。
故答案为:B
【点睛】此题主要考查长方体的棱长总和公式的灵活运用,按比例分配的方法及应用,关键是熟记公式。
5.D
【分析】交换真分数分子和分母的位置,即可得到它的倒数,整数的倒数是这个整数分之一,据此确定甲数和乙数,求和,再根据求一个数的百分之几是多少,用乘法计算即可。
【详解】(+)×25%
=×
=
甲数的倒数是,乙数的倒数是4,甲、乙两数和的25%是。
故答案为:D
【点睛】关键是理解倒数的含义,掌握求一个数的百分之几是多少的方法。
6.A
【分析】降价钱数+现价=原价,降价钱数÷原价=比原价降低了百分之几,据此列式计算。
【详解】20÷(20+180)
=20÷200
=0.1
=10%
比原价降低了10%。
故答案为:A
【点睛】此类问题一般用表示单位“1”的量作除数。
7.14
【分析】设四人为a,b,c,d,单人照有4种:a,b,c,d;两人合影有6种:ab,ac,ad,bc,bd,cd;三人合影有4种:abc,abd,acd,bcd;所以一共有(4+6+4)种。
【详解】4+6+4=14(张)
他们一共要拍14张照片。
8.67
【分析】每人3个还剩10个,10-3=7,也就是这批苹果的数量是3的倍数还多7;每人4个还剩11个,11-4=7,也就是这批苹果的数量是4的倍数还多7;每人5个还剩12个,12-5=7,所以这批数量是5的倍数多7。这批苹果的数量是3、4、5的公倍数多7;因为3、4、5两两互质,则用3×4×5即可求出这三个数的最小公倍数,再加上7即可求出这批苹果的数量最少是多少。
【详解】10-3=7
11-4=7
12-5=7
3×4×5=60
60+7=67(个)
这箱苹果至少有67个。
【点睛】本题主要考查了最小公倍数的灵活应用,找到相同的余数是解答本题的关键。
9.16
【分析】小红和小明看到的全班的人数总和是总共人数-1且是不变的,也就是他们看到的总人数。以他们看到的总人数为单位“1”,小红看到不戴眼镜的同学是戴眼镜同学的2倍,戴眼镜的人数是1份,那么不带眼镜的人数就是2份,戴眼镜占他们看到的总人数的。小明看到戴眼镜的同学是不戴眼镜同学的,则戴眼镜的同学是2份,不戴眼镜的同学是3份,戴眼镜占他们看到的总人数的。如果小红和小明两个人都戴眼镜或都不戴眼镜,看到的比例分数应该是一样,但是小明看到的比小红比例多,则小明不戴眼镜,小红戴眼镜,也就是小明看到的戴眼镜的比小红看到的戴眼镜的多1人,多的1人正好是他们看到的总人数的。那么看到的人数为15人。注意最后还要加上1(也就是自己)。
【详解】
=
1÷=15(名)
15+1=16(名)
参加联欢会的同学共有16名。
10. 45 等腰直角/等腰
【分析】由题意可知,已知是直角三角形,一个锐角是45°,根据三角形的内角和是180°,即可计算出另一个锐角的度数,然后比较两个锐角的大小,再根据等腰三角形的性质判断即可。
【详解】180°-90°-45°
=90°-45°
=45°
所以另一个锐角是45°,两个锐角相等,这也是一个等腰直角三角形。
11. 5∶2∶3 4
【分析】观察图形可知,平行四边形底是(2+3)cm,根据平行四边形面积公式:面积=底×高;高=面积÷底,代入数据,求出平行四边形的高;甲、乙、丙三个三角形的高等于平行四边形的高,甲的底等于平行四边形的底,根据三角形面积公式:面积=底×高÷2,代入数据,求出甲、乙、丙三个三角形面积,再根据比的意义,用甲的面积∶乙的面积∶丙的面积,求出三个三角形面积比;涂色部分等于乙三角形面积,据此解答。
【详解】高:20÷(2+3)
=20÷5
=4(cm)
甲:(2+3)×4÷2
=5×4÷2
=20÷2
=10(cm2)
乙:2×4÷2
=8÷2
=4(cm2)
丙:3×4÷2
=12÷2
=6(cm2)
10∶4∶6
=(10÷2)∶(4÷2)∶(6÷2)
=5∶2∶3
涂色面积是4cm2。
如图,平行四边形的面积是20cm2,图中甲、乙、丙三个三角形的面积比是5∶2∶3,涂色部分的面积是4cm2。
12.1∶300000/
【分析】先统一单位,再根据比例尺=图上距离∶实际距离,写出这幅图的比例尺即可。
【详解】15千米=1500000厘米
5厘米∶1500000厘米
=(5÷5)∶(1500000÷5)
=1∶300000
这幅图的比例尺是1∶300000。
【点睛】本题主要考查了比例尺的意义,注意单位要统一。
13. 25 5
【分析】设2元的人民币有x张,则5元的人民币(30-x)张,又知“合计人民币75元”,可得等量关系式:面值2元的人民币×张数+面值5元的人民币×张数=75,据此等量列方程解答。
【详解】解:设2元的人民币有x张,则5元的人民币(30-x)张,由题意得:
2x+5(30-x)=75
2x+150-5x=75
2x+150-5x-2x=75-2x
150-5x=75-2x
150-5x+5x=75-2x+5x
150=75+3x
150-75=75+3x-75
3x=75
3x÷3=75÷3
x=25
30-x
=30-25
=5(张)
2元的25张,5元的5张。
【点睛】鸡兔同笼问题用方程解答容易想,根据其中一个等量关系表示两个未知量,另一个等量关系列方程。
14. 169.56 56.52
【分析】把正方体削成一个最大的圆柱,则这个圆柱的底面直径是6厘米,高是6厘米,根据圆柱的体积公式:V=πr2h,用3.14×(6÷2)2×6即可求出圆柱的体积;再把圆柱削成一个最大的圆锥,则这个圆锥的底面直径是6厘米,高是6厘米,根据圆锥的体积公式:V=πr2h,用×3.14×(6÷2)2×6即可求出圆锥的体积。
【详解】3.14×(6÷2)2×6
=3.14×32×6
=3.14×9×6
=169.56(立方厘米)
169.5656.52(立方厘米)
圆柱的体积是169.56立方厘米,圆锥的体积是56.52立方厘米。
【点睛】本题主要考查了圆柱体积公式和圆锥体积公式的应用。
15.√
【分析】可以用求比值的方法:两个比的比值相等,就能组成比例,比值不相等,就不能组成比例;也可以根据比例的性质:两外项的积等于两内项的积,据此逐项分析再选择。
【详解】因42×1=42,4×10.5=42,所以42∶4和10.5∶1能组成比例。故原题说法正确。
故答案为:√
【点睛】本题主要考查了比的意义及基本性质的灵活运用。
16.√
【分析】小数的整数部分从右边起,分别是个位、十位、百位……小数部分从左边起,分别是十分位、百分位、千分位……十分位的计数单位是十分之一,百分位的计数单位是百分之一,千分位的计数单位是千分之一……据此解答即可。
【详解】0.074中的“7”在百分位上,表示7个百分之一。原题说法正确。
故答案为:√
【点睛】此题考查小数的数位和计数单位,要熟练掌握。
17.×
【分析】根据题意,正品率=正品数量÷总数量×100%,由此代入数据判断。
【详解】100÷(100+4)×100%
=100÷104×100%
≈96.2%
96.2%<100%
一批零件里100件正品,4件次品,正品率约96.2%,为原题说法错误;
故答案为:×
【点睛】此题属于百分率问题,都是用一部分数量(或全部数量)除以全部数量乘100%。
18.×
【分析】用10℃和0℃相差10℃,用﹣7℃和0℃相差7℃,用10℃+7℃即可求出这两个温度相差多少。
【详解】10℃+7℃=17℃
所以10℃比﹣7°C高17℃。
所以题干说法是错误的。
故答案为:×
【点睛】熟练掌握正、负数的运算方法,是解答此题的关键。
19.√
【分析】每个点都可以和另外7个点连成7条线段,共能连成8×7=56(条)线段,由于每条线段重复计算了一次,所以共能连成56÷2=28(条)线段;据此解答即可。
【详解】8×(8-1)÷2
=8×7÷2
=56÷2
=28(条)
即这8个点可以构成28条线段,所以原题说法正确。
故答案为:√
【点睛】本题考查了线段的计数问题,实质是握手问题,可以直接根据计算公式解答。
20.763;81.25;10;90
;1010;0.16;
【详解】略
21.(1)0.5;(2)36;(3)83
【分析】(1)先算小括号里面的减法,再按照从左向右的顺序进行计算;
(2)先算小括号里面的减法,再算中括号里面的乘法,最后算括号外面的除法;
(3)先根据积不变性质,将算式变为8.3×9.8+0.2×8.3,然后根据乘法分配律,将算式变为8.3×(9.8+0.2)进行计算。
【详解】(1)1.05×(3.8-0.8)÷6.3
=1.05×3÷6.3
=3.15÷6.3
=0.5
(2)44÷[(-)×2]
=44÷[×2]
=44÷
=44×
=36
(3)8.3×9.8+2×0.83
=8.3×9.8+0.2×8.3
=8.3×(9.8+0.2)
=8.8×10
=83
22.x=;x=18;x=0.5
【分析】(1)先化简,然后再根据等式的性质,方程两边同时除以求解;
(2)把比例化成一般方程0.2x=0.45×8,再根据等式的性质,方程两边同时除以0.2即可得到原比例的解;
(3)再根据等式的性质,方程两边同时减去1.25,然后再同时除以5求解。
【详解】x-x=
解:x=
x÷=÷
x=×6
x=
0.45∶x=0.2∶8
解:0.2x=0.45×8
0.2x=3.6
0.2x÷0.2=3.6÷0.2
x=18
5x+1.25=3.75
解:5x+1.25-1.25=3.75-1.25
5x=2.5
5x÷5=2.5÷5
x=0.5
23.13.5平方厘米
【分析】根据图示,先求出三角形的底(也就是半圆的直径),然后用半圆的面积减去三角形的面积即可;三角形的底=三角形的面积×2÷高,先利用两条直角边求出三角形的面积,再代入公式求出三角形的底边;圆的面积=πr 。
【详解】三角形的底(也就是半圆的直径)是:
8×6÷2×2÷4.8
=48÷4.8
=10(厘米)
阴影部分的面积:
3×(10÷2)2÷2-8×6÷2
=3×25÷2-24
=37.5-24
=13.5(平方厘米)
阴影部分的面积是13.5平方厘米。
24.C商场
【分析】A商场:每满100元返20元,根据单价×数量=总价,代入求出60瓶这种饮料的原价,计算原价里面有多少个100元,就减多少个20元,用原价减去优惠的价格,即可求出A商场优惠后的价格。
B商场:八五折=85%,先根据单价×数量=总价,代入求出60瓶这种饮料的原价,乘折扣85%,即可求出B商场优惠后的价格;
C商场:买10送2,先计算60个里面有多少个(10+2),即送多少个2,求出购买的实际数量,再乘饮料的单价,即可求出C商场优惠后的价格;比较三家商场优惠后价格即可得解。
【详解】A商场:4.5×60÷100≈2(个)
4.5×60-2×20
=270-40
=230(元)
B商场:
4.5×60×85%
=270×85%
=229.5(元)
C商场:
60÷(10+2)
=60÷12
=5(个)
60-2×5
=60-10
=50(瓶)
4.5×50=225(元)
225<229.5<230
答:C商场更省钱。
【点睛】最优化问题常用比较法进行解答,分别计算出三种方案优惠后的价格,再进行比较。
25.4.5个小时
【分析】由题意可知,去时和返回的路程不变,根据速度×时间=路程,则速度和时间成反比例,据此列比例解答即可。
【详解】解:设x小时能够返回原地。
80x=72×5
80x=360
80x÷80=360÷80
x=4.5
答:需要4.5个小时。
【点睛】本题考查用比例解决实际问题,明确速度和时间成反比例是解题的关键。
26.39.564吨
【分析】根据圆的周长公式:C=2πr,据此求出圆锥底面的半径,再根据圆锥的体积公式:V=πr2h,据此求出这堆煤的体积,再乘1.4即可求解。
【详解】18.84÷3.14÷2
=6÷2
=3(米),
3.14×32×3×
=3.14×9×(3×)
=28.26×1
=28.26(立方米)
28.26×1.4=39.564(吨)
答:这堆煤约重39.564吨。
【点睛】本题考查圆锥的体积,熟记公式是解题的关键。
27.1256毫升
【分析】瓶子的底面直径和正放时液面的高度已知,根据圆柱的体积公式:V=,则可以求出瓶内液体的体积,同样的方法,可以求出倒放时空余部分的体积,瓶子的容积=饮料的体积+倒放时空余部分的体积。据此解答。
【详解】8÷2=4(厘米)
3.14×42×7+3.14×42×18
=3.14×16×7+3.14×16×18
=351.68+904.32
=1256(立方厘米)
=1256(毫升)
答:这个瓶子的容积是1256毫升。
【点睛】此题解答关键是利用体积不变的特性,把不规则图形转化为规则图形来计算。
28.44千米
【分析】根据题意,甲、乙两人的速度比为3∶2,当两人用的时间相同时,甲、乙两人的路程比等于速度比3∶2,即甲走的路程是乙路程的;先求出乙行了5.5千米的时间,甲行了5.5×=8.25千米,而实际甲行了11千米,说明甲比乙先行11-8.25=2.75千米;
又已知当甲到达B地时,乙离B地还有的路程,把全程看作单位“1”,则乙行了全程的(1-),而甲行的路程是乙的,所以甲行了全程的(1-)×=;那么甲先行的路程占全程的(1-),单位“1”未知,用甲先行的路程除以(1-),即可求出AB两地的距离。
【详解】当乙行了5.5千米时,甲只能行:
5.5×=8.25(千米)
所以甲比乙先行:11-8.25=2.75(千米)
当乙离B地还有的路程时,甲行了全程的:
(1-)×
=×
=
全程:
2.75÷(1-)
=2.75÷
=2.75×16
=44(千米)
答:AB两地相距44千米。
【点睛】本题考查分数除法的实际应用,先把比转化成分数,明确时间相同时,两人的路程比等于他们的速度比;分析出甲先行的路程占全程的几分之几,然后根据分数除法的意义解答。
29.(1)见解答
(2)16,87
(3)43
(4)11.1%
【分析】(1)阴影条形每天都比空白条形高,所以阴影条形表示乳酪蛋糕,空白条形表示奶油蛋糕。
(2)奶油蛋糕16日的销售量最多。18日奶油蛋糕和乳酪蛋糕一共销售多少个用加法计算。
(3)五天的乳酪蛋糕的和除以天数就得平均数。
(4)用16日的奶油蛋糕数量减去19日的奶油蛋糕数量再除以16日的奶油蛋糕数量。
【详解】(1)如图:
(2)35+52=87(个)
奶油蛋糕16日的销售量最多。18日奶油蛋糕和乳酪蛋糕一共销售87个。
(3)(38+45+52+41+39)÷5
=215÷5
=43(个)
这5天乳酪蛋糕平均每日销售43个。
(4)(36-32)÷36
=4÷36
≈11.1%
答:19日销售的奶油蛋糕比16日的奶油蛋糕减少了11.1%。
【点睛】本题考查了学生对统计图意义的掌握及从统计图中获取信息的意识。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
