苏教版五年级数学上册平行四边形的面积(无答案)
文档属性
| 名称 | 苏教版五年级数学上册平行四边形的面积(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 329.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-06 15:01:42 | ||
图片预览

文档简介
1.平行四边形的面积
[基础巩固]
1.知识点:平行四边形面积的计算方法
(1)长方形的面积= 长 × 宽
平行四边形的面积= ( ) × ( )
(2)平行四边形的面积用字母表示:( )。
我发现:可以用割补的方法把平行四边形转化成长方形。割补前后,图形的面积( ),周长( )。(填“变大”“变小”或“不变”)
2.把平行四边形沿( )剪开平移,拼成一个长方形,长方形的长与平行四边形的( )相等,长方形的宽与平行四边形的( )相等,长方形和平行四边形的( )也相等。因为长方形的面积等于( )乘以( ),所以平行四边形的面积等于( )乘以( ),用字母表示为( )。
[学以致用]
一、填一填。
1.一块平行四边形草地的面积是120平方米,底是15米,高是( )米。
2.一个平行四边形的底是80厘米,高是4分米,它的面积是( )平方分米。
3.一张平行四边形卡片的底是16厘米,高比底少4厘米,它的面积是( )平方厘米。
4.一个平行四边形的面积是22平方分米,高是11分米,底是( )分米。
5.一个平行四边形的底是12分米,高是底的一半,这个平行四边形的面积是( )平方分米。
6.一个平行四边形的底是20厘米,是高的一半。这个平行四边形的面积是( )平方厘米。
二、判断题。
1.平行四边形的底越长,它的面积越大。( )
2.两个等底等高的平行四边形,形状不一定完全相同。( )
3.平行四边形的底不变,高扩大为原来的3倍,它的面积也扩大为原来的3倍。( )
4.形状不同的两个平行四边形的面积一定不会相等。( )
三、选择题。
1.把平行四边形分成两部分,再拼成长方形。这两部分可能是( )。
A.一个直角三角形和一个直角梯形 B.两个直角三角形或两个直角梯形
C.两个一般梯形 D.两个一般三角形
2.下面说法正确的是( )。
A.平行四边形的高越长,面积越大
B.一个平行四边形的底和高同时扩大到原来的3倍,面积扩大到原来的6倍
C.等底等高的平行四边形面积相等 D.形状不同的平行四边形,面积不相等
3.把一个长方形框架拉成一个平行四边形,这个平行四边形与原来的长方形相比,周长( ),面积( )。 A.变大 B.变小 C.不变
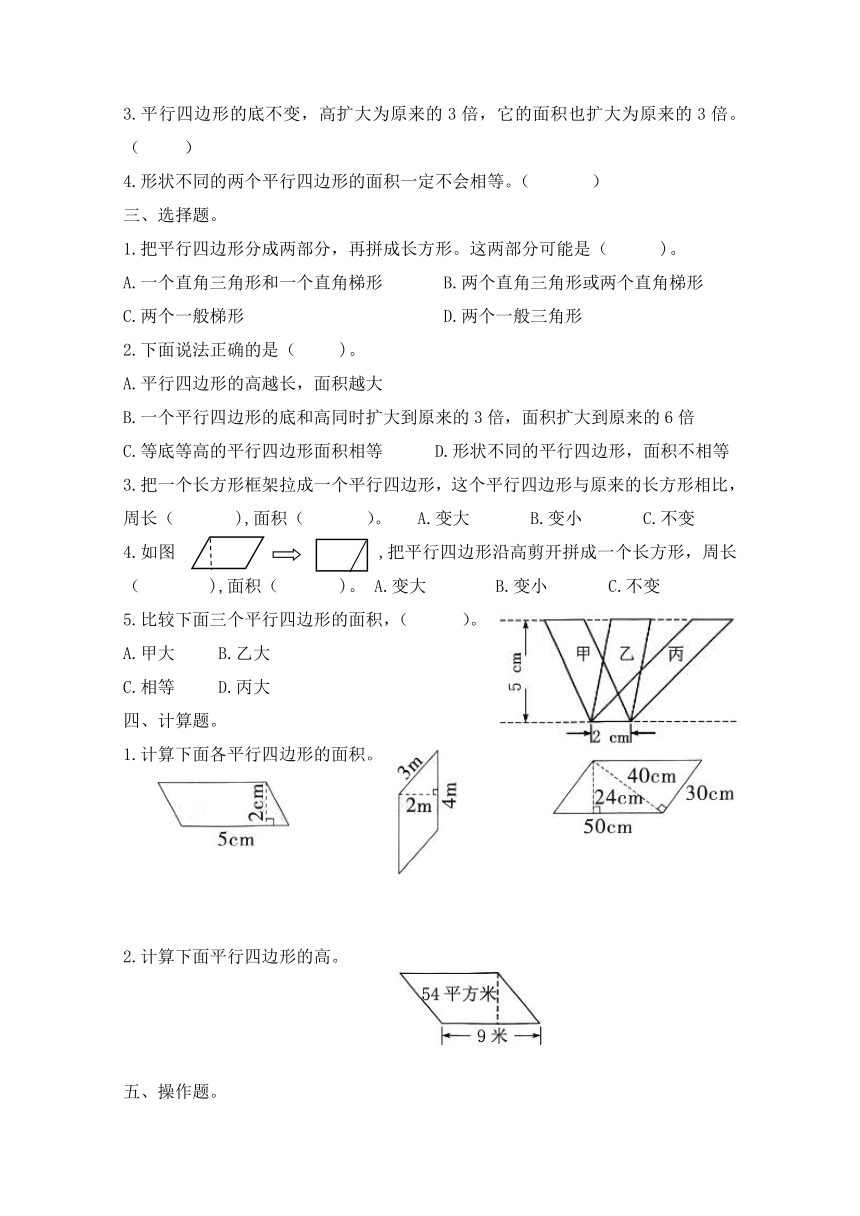
4.如图 ,把平行四边形沿高剪开拼成一个长方形,周长( ),面积( )。 A.变大 B.变小 C.不变
5.比较下面三个平行四边形的面积,( )。
A.甲大 B.乙大
C.相等 D.丙大
四、计算题。
1.计算下面各平行四边形的面积。
2.计算下面平行四边形的高。
五、操作题。
1.下面每个方格的面积都是1平方厘米,在方格图中画三个形状不同的平行四边形,面积都是12平方厘米。
2.在下面的方格图中画出两个形状不同的平行四边形,使它们的面积和图中长方形的面积相等。
六、解决问题。
1.有一块近似平行四边形的果园地,底是200米,底比高少50米。这个果园的面积是多少?
2.一个底为5米、高为3米的平行四边形广告牌,在它的正反两面刷上油漆,油漆面积是多少平方米?
3.王大爷家有一块底是60米,高是45米的平行四边形地。
(1)每平方米可以种6棵白菜,这块地一共可以种多少棵白菜?
(2)如果改栽果树,每棵果树占地5平方米,这块地一共能栽多少棵果树?
4.一块平行四边形水稻地,底为80米,高为30米,每100平方米大约可收获稻谷120千克。这块地大约可收获稻谷多少千克?
5.一个平行四边形,若底不变,高增加4厘米,则面积增加36平方厘米;若高不变,底增加5厘米,则面积增加20平方厘米。求原来平行四边形的面积。
6.一个平行四边形,相邻的两条边分别为6厘米和9厘米,其中一条边上的高为6厘米,求这个平行四边形的面积。(不考虑长方形的情况)
[思维拓展]
1.小明用木条做了一个底是18厘米、高是10厘米的平行四边形,把它拉成一个长方形后,面积增加了36平方厘米,长方形的周长是( )厘米。
2.用多长的铁丝正好能围成这个平行四边形?
3.如图,正方形的周长是36厘米,三角形①的面积是28平方厘米,求涂色部分的面积。
4.如图,平行四边形(涂色部分)的面积是48平方厘米,大正方形的面积是64平方厘米。小正方形的边长是多少厘米?
5.敏敏有一张长是宽的2倍,周长是24分米的长方形纸(如下图)。她在这张纸上剪掉2个等腰直角三角形后,剩余部分是一个平行四边形,求这个平行四边形的面积。
6.将平行四边形用两条相交线分成4个小平行四边形,已知底和高。(如图①)
(1)请比较S1×S3与S2×S4的大小。(S1、S3、S2、S4均指各自所在图形的面积)
(2)根据第(1)题的结论,图②中涂色部分的面积是( )平方厘米。
[基础巩固]
1.知识点:平行四边形面积的计算方法
(1)长方形的面积= 长 × 宽
平行四边形的面积= ( ) × ( )
(2)平行四边形的面积用字母表示:( )。
我发现:可以用割补的方法把平行四边形转化成长方形。割补前后,图形的面积( ),周长( )。(填“变大”“变小”或“不变”)
2.把平行四边形沿( )剪开平移,拼成一个长方形,长方形的长与平行四边形的( )相等,长方形的宽与平行四边形的( )相等,长方形和平行四边形的( )也相等。因为长方形的面积等于( )乘以( ),所以平行四边形的面积等于( )乘以( ),用字母表示为( )。
[学以致用]
一、填一填。
1.一块平行四边形草地的面积是120平方米,底是15米,高是( )米。
2.一个平行四边形的底是80厘米,高是4分米,它的面积是( )平方分米。
3.一张平行四边形卡片的底是16厘米,高比底少4厘米,它的面积是( )平方厘米。
4.一个平行四边形的面积是22平方分米,高是11分米,底是( )分米。
5.一个平行四边形的底是12分米,高是底的一半,这个平行四边形的面积是( )平方分米。
6.一个平行四边形的底是20厘米,是高的一半。这个平行四边形的面积是( )平方厘米。
二、判断题。
1.平行四边形的底越长,它的面积越大。( )
2.两个等底等高的平行四边形,形状不一定完全相同。( )
3.平行四边形的底不变,高扩大为原来的3倍,它的面积也扩大为原来的3倍。( )
4.形状不同的两个平行四边形的面积一定不会相等。( )
三、选择题。
1.把平行四边形分成两部分,再拼成长方形。这两部分可能是( )。
A.一个直角三角形和一个直角梯形 B.两个直角三角形或两个直角梯形
C.两个一般梯形 D.两个一般三角形
2.下面说法正确的是( )。
A.平行四边形的高越长,面积越大
B.一个平行四边形的底和高同时扩大到原来的3倍,面积扩大到原来的6倍
C.等底等高的平行四边形面积相等 D.形状不同的平行四边形,面积不相等
3.把一个长方形框架拉成一个平行四边形,这个平行四边形与原来的长方形相比,周长( ),面积( )。 A.变大 B.变小 C.不变
4.如图 ,把平行四边形沿高剪开拼成一个长方形,周长( ),面积( )。 A.变大 B.变小 C.不变
5.比较下面三个平行四边形的面积,( )。
A.甲大 B.乙大
C.相等 D.丙大
四、计算题。
1.计算下面各平行四边形的面积。
2.计算下面平行四边形的高。
五、操作题。
1.下面每个方格的面积都是1平方厘米,在方格图中画三个形状不同的平行四边形,面积都是12平方厘米。
2.在下面的方格图中画出两个形状不同的平行四边形,使它们的面积和图中长方形的面积相等。
六、解决问题。
1.有一块近似平行四边形的果园地,底是200米,底比高少50米。这个果园的面积是多少?
2.一个底为5米、高为3米的平行四边形广告牌,在它的正反两面刷上油漆,油漆面积是多少平方米?
3.王大爷家有一块底是60米,高是45米的平行四边形地。
(1)每平方米可以种6棵白菜,这块地一共可以种多少棵白菜?
(2)如果改栽果树,每棵果树占地5平方米,这块地一共能栽多少棵果树?
4.一块平行四边形水稻地,底为80米,高为30米,每100平方米大约可收获稻谷120千克。这块地大约可收获稻谷多少千克?
5.一个平行四边形,若底不变,高增加4厘米,则面积增加36平方厘米;若高不变,底增加5厘米,则面积增加20平方厘米。求原来平行四边形的面积。
6.一个平行四边形,相邻的两条边分别为6厘米和9厘米,其中一条边上的高为6厘米,求这个平行四边形的面积。(不考虑长方形的情况)
[思维拓展]
1.小明用木条做了一个底是18厘米、高是10厘米的平行四边形,把它拉成一个长方形后,面积增加了36平方厘米,长方形的周长是( )厘米。
2.用多长的铁丝正好能围成这个平行四边形?
3.如图,正方形的周长是36厘米,三角形①的面积是28平方厘米,求涂色部分的面积。
4.如图,平行四边形(涂色部分)的面积是48平方厘米,大正方形的面积是64平方厘米。小正方形的边长是多少厘米?
5.敏敏有一张长是宽的2倍,周长是24分米的长方形纸(如下图)。她在这张纸上剪掉2个等腰直角三角形后,剩余部分是一个平行四边形,求这个平行四边形的面积。
6.将平行四边形用两条相交线分成4个小平行四边形,已知底和高。(如图①)
(1)请比较S1×S3与S2×S4的大小。(S1、S3、S2、S4均指各自所在图形的面积)
(2)根据第(1)题的结论,图②中涂色部分的面积是( )平方厘米。
