选择必修 第二章 2.3.3 点到直线的距离公式 课件(共25张PPT)
文档属性
| 名称 | 选择必修 第二章 2.3.3 点到直线的距离公式 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-08 17:45:51 | ||
图片预览







文档简介
(共25张PPT)
选择必修
第二章 直线和圆的方程
2.3 直线的交点坐标与距离公式
2.3.3 点到直线的距离公式
教学目标
学习目标 数学素养
1.理解点到直线距离公式的推导过程,掌握点到直线的距离公式. 1.直观想象素养和逻辑推理素养.
2.会用点到直线的距离公式分析解决问题. 2.数形结合素养和数学运算素养.
温故知新
2.利用“坐标法”解决平面几何问题的基本步骤:
1. 两点间的距离公式:
平面内两点 P1 (x1,y1),P2 (x2,y2),
.
① 原点 O (0,0) 与任一点 P (x,y) 间的距离:.
② 当直线P1P2垂直于x轴时:|| = ||;
③ 当直线P1P2垂直于y轴时:|| = ||.
第一步:建立坐标系,用坐标表示有关的量;
第二步:进行有关的代数运算
第三步:把代数运算的结果“翻译”成几何结论
新知引入
在公路附近有一家乡村饭馆,现在需要铺设一条连接饭馆和公路的道路.请同学们帮助设计一下:在理论上怎样铺路可以使这条连接道路的长度最短
新知探究
点P到直线l的距离,就是从点P到直线l的垂线段PQ的长度,其中Q是垂足
(如图).因此,求出垂足Q的坐标,利用两点间的距离公式求出|PQ|,就可以得到点P到直线l的距离.
,于是,
如图,已知点P(x0,y0),直线l:Ax+By+C=0,
如何求点P到直线l的距离?
P
Q
x
y
O
l
新知探究
设A≠0,B≠0,由PQ⊥l,以及直线l的斜率为-,可得垂线PQ的斜率为,因此,垂线PQ的方程为y-y0=(x-x0),即Bx-Ay=Bx0-Ay0.
解方程组,
方法1:(坐标法)
P
Q
x
y
O
l
得直线l与PQ的交点坐标,即垂足Q的坐标为
.
于是
.
.
因此,点P(x0,y0)到直线l:Ax+By+C=0的距离
可以验证,当A=0,或B=0时,上述公式仍然成立.
新知探究
上述方法中,我们根据点到直线距离的定义,将点到直线的距离转化为两点之间的距离,思路自然但运算量较大.反思求解过程,你发现引起复杂运算的原因了吗?由此能否给出简化运算的方法?
上述方法中,若设垂直Q的坐标为(x,y),则
. ①
对于①式,你能给出它的几何意义吗?能否直接求出(x-x0)2+(y-y0)2,进而求出|PQ|呢?请你试一试!
新知探究
设A≠0,B≠0,由PQ⊥l,以及直线l的斜率为-,可得垂线PQ的斜率为,因此,垂线PQ的方程为y-y0=(x-x0),即Bx-Ay=Bx0-Ay0.
解方程组,转化为的方程组
方法2:(整体法)
P
Q
x
y
O
l
,
③④两边分别平方后相加,得.
,
可以验证,当A=0,或B=0时,上述公式仍然成立.
即.
∴=.
新知探究
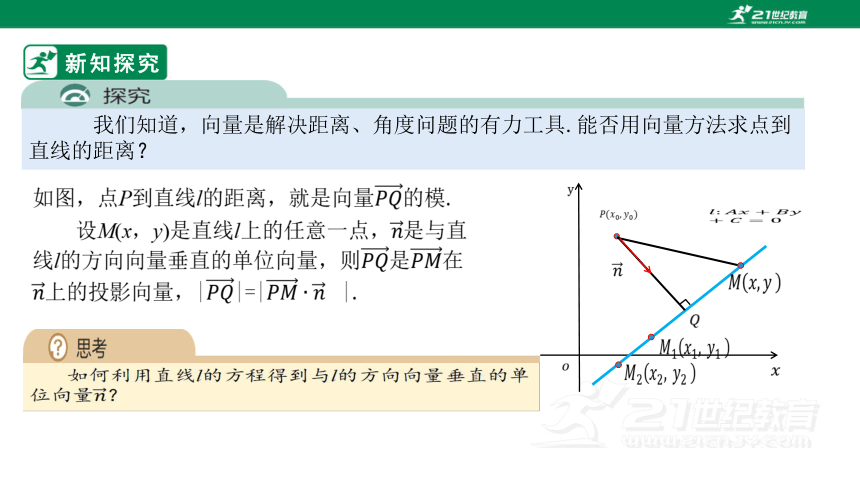
我们知道,向量是解决距离、角度问题的有力工具.能否用向量方法求点到直线的距离?
如图,点P到直线l的距离,就是向量的模.
设M(x,y)是直线l上的任意一点,是与直线l的方向向量垂直的单位向量,则是在
上的投影向量,||=| |.
如何利用直线l的方程得到与l的方向向量垂直的单位向量?
新知探究
方法3:(向量法)
设M1(x1,y1),M2(x2,y2)是直线Ax+By+C=0上任意两点,则是直线l的方向向量.
把Ax1+By1+C=0,Ax2+By2+C=0两式相减,得
A(x2-x1)+B(y2-y1)=0.
由向量的数量积运算可知,向量(A,B)与向量(x2-x1,y2-y1)垂直.
则向量就是与直线l的方向向量垂直的单位向量.
新知探究
取,
.
.
∵点M(x,y)在直线l上,∴Ax+By+C=0,即Ax+By=-C.
∴.
因此.
从而
新知探究
,
求PM最短线段的长度|PQ|,即求d的最小值.
虽然思路简单,但运算繁琐.
比较上述几种方法,第一种方法从定义出发,把问题转化为求两点间的距离,通过代数运算得到结果;最后一种方法利用向量投影,通过向量运算求出结果,简化了运算.除了上述方法,你还有其他推导方法吗?
方法4:(函数法)
新知探究
点P(x0,y0)到直线l:Ax+By+C=0的距离:
注意:用此公式时,直线方程必须先化成一般式.
点到直线的距离公式.
.
分子是P点坐标代入直线方程左边
分母是直线未知数x、y系数平方和的算术根
知新探究
【例1】求点P(-1,2)到直线l:3x=2的距离.
解:
方法1:点P(-1,2)到直线l:3x-2=0的距离
方法2:由直线l可得,,
.
∴点P(-1,2)到直线l:3x=2的距离
分析:将直线l的方程写成3x-2=0,再用点到直线的距离公式求解.
直线l有什么特性?
由此你能给出简便解法吗?
.
初试身手
1.求点P(3,-2)到下列直线的距离:
⑴; ⑵y=3; ⑶x=-1.
解:
⑴∵直线可化为3x-4y+1=0,
∴点P(3,-2)到直线的距离
.
⑵点P(3,-2)到直线y=3的距离
.
⑶点P(3,-2)到直线x=-1的距离
.
知新探究
【例2】已知△ABC的三个顶点分别是A(1,3),B(3,1),C(-1,0),求△ABC的面积.
解:
如图,设AB边上的高为h,则
,
|AB|=,
边AB上的高为h就是点C到直线AB的距离.
边AB所在直线l的方程为,
即,
∴点C(-1,0)到x+y-4=0的距离.
因此,.
分析:由三角形面积公式可知,只有利用距离公式求出边AB的长和边AB上的高即可.
你还有其他解法吗?
初试身手
解:
由直线方程的两点式得直线BC的方程为,
即x-2y+3=0,
点A到BC的距离为d,即为BC边上的高,
.
由两点间距离公式得
2.已知点A(-1,3), B(-3,0), C(1,2),求△ABC的面积.
|BC|=.
∴=4.
新知探究
【例3】已知点P(2,-1),求过点P且与原点距离为2的直线l的方程.
当直线l的斜率不存在时,直线l的方程为x=2,符合题意;
当直线l的斜率存在时,设直线l的方程为y+1=k(x-2),
即kx-y-2k-1=0,
,
∴直线l的方程为y+1=(x-2),即3x-4y-10=0.
由点到直线距离公式得,
解:
解得,
故直线l的方程为x=2或3x-4y-10=0.
初试身手
3.求过点M(-2,1),且与A(-1,2),B(3,0)两点距离相等的直线l的方程..
解:
方法1:当直线l斜率不存在时,不存在符合题意的直线.
当直线l斜率存在时,设所求的直线方程为y-1=k(x+2),
即kx-y+2k+1=0,
由题意得
解得k=0或k=.
故所求的直线l方程为y=1或x+2y=0.
初试身手
3.求过点M(-2,1),且与A(-1,2),B(3,0)两点距离相等的直线l的方程..
解:
方法2:由平面几何知识,得l∥AB或l过AB中点.
若l∥AB,
∵kAB=,且直线l过点M(-2,1),
∴直线l方程为x+2y=0
若l过AB的中点N(1,1),又直线l过点M(-2,1),则l的方程为y=1.
故所求的直线l方程为y=1或x+2y=0.
课堂小结
点P(x0,y0)到直线l:Ax+By+C=0的距离:
.
点到直线的距离公式.
应用点到直线的距离公式的关注点:
⑴直线方程应为一般式,若给出其他形式应化为一般式;
⑵直线方程Ax+By+C=0中,A=0或B=0公式也成立;
⑶点P在直线l上时,点到直线的距离为0,公式仍然适用.
作业布置
作业: P77 练习 第2⑵⑶,3题
P79-80 习题2.3 第6,13,14题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
选择必修
第二章 直线和圆的方程
2.3 直线的交点坐标与距离公式
2.3.3 点到直线的距离公式
教学目标
学习目标 数学素养
1.理解点到直线距离公式的推导过程,掌握点到直线的距离公式. 1.直观想象素养和逻辑推理素养.
2.会用点到直线的距离公式分析解决问题. 2.数形结合素养和数学运算素养.
温故知新
2.利用“坐标法”解决平面几何问题的基本步骤:
1. 两点间的距离公式:
平面内两点 P1 (x1,y1),P2 (x2,y2),
.
① 原点 O (0,0) 与任一点 P (x,y) 间的距离:.
② 当直线P1P2垂直于x轴时:|| = ||;
③ 当直线P1P2垂直于y轴时:|| = ||.
第一步:建立坐标系,用坐标表示有关的量;
第二步:进行有关的代数运算
第三步:把代数运算的结果“翻译”成几何结论
新知引入
在公路附近有一家乡村饭馆,现在需要铺设一条连接饭馆和公路的道路.请同学们帮助设计一下:在理论上怎样铺路可以使这条连接道路的长度最短
新知探究
点P到直线l的距离,就是从点P到直线l的垂线段PQ的长度,其中Q是垂足
(如图).因此,求出垂足Q的坐标,利用两点间的距离公式求出|PQ|,就可以得到点P到直线l的距离.
,于是,
如图,已知点P(x0,y0),直线l:Ax+By+C=0,
如何求点P到直线l的距离?
P
Q
x
y
O
l
新知探究
设A≠0,B≠0,由PQ⊥l,以及直线l的斜率为-,可得垂线PQ的斜率为,因此,垂线PQ的方程为y-y0=(x-x0),即Bx-Ay=Bx0-Ay0.
解方程组,
方法1:(坐标法)
P
Q
x
y
O
l
得直线l与PQ的交点坐标,即垂足Q的坐标为
.
于是
.
.
因此,点P(x0,y0)到直线l:Ax+By+C=0的距离
可以验证,当A=0,或B=0时,上述公式仍然成立.
新知探究
上述方法中,我们根据点到直线距离的定义,将点到直线的距离转化为两点之间的距离,思路自然但运算量较大.反思求解过程,你发现引起复杂运算的原因了吗?由此能否给出简化运算的方法?
上述方法中,若设垂直Q的坐标为(x,y),则
. ①
对于①式,你能给出它的几何意义吗?能否直接求出(x-x0)2+(y-y0)2,进而求出|PQ|呢?请你试一试!
新知探究
设A≠0,B≠0,由PQ⊥l,以及直线l的斜率为-,可得垂线PQ的斜率为,因此,垂线PQ的方程为y-y0=(x-x0),即Bx-Ay=Bx0-Ay0.
解方程组,转化为的方程组
方法2:(整体法)
P
Q
x
y
O
l
,
③④两边分别平方后相加,得.
,
可以验证,当A=0,或B=0时,上述公式仍然成立.
即.
∴=.
新知探究
我们知道,向量是解决距离、角度问题的有力工具.能否用向量方法求点到直线的距离?
如图,点P到直线l的距离,就是向量的模.
设M(x,y)是直线l上的任意一点,是与直线l的方向向量垂直的单位向量,则是在
上的投影向量,||=| |.
如何利用直线l的方程得到与l的方向向量垂直的单位向量?
新知探究
方法3:(向量法)
设M1(x1,y1),M2(x2,y2)是直线Ax+By+C=0上任意两点,则是直线l的方向向量.
把Ax1+By1+C=0,Ax2+By2+C=0两式相减,得
A(x2-x1)+B(y2-y1)=0.
由向量的数量积运算可知,向量(A,B)与向量(x2-x1,y2-y1)垂直.
则向量就是与直线l的方向向量垂直的单位向量.
新知探究
取,
.
.
∵点M(x,y)在直线l上,∴Ax+By+C=0,即Ax+By=-C.
∴.
因此.
从而
新知探究
,
求PM最短线段的长度|PQ|,即求d的最小值.
虽然思路简单,但运算繁琐.
比较上述几种方法,第一种方法从定义出发,把问题转化为求两点间的距离,通过代数运算得到结果;最后一种方法利用向量投影,通过向量运算求出结果,简化了运算.除了上述方法,你还有其他推导方法吗?
方法4:(函数法)
新知探究
点P(x0,y0)到直线l:Ax+By+C=0的距离:
注意:用此公式时,直线方程必须先化成一般式.
点到直线的距离公式.
.
分子是P点坐标代入直线方程左边
分母是直线未知数x、y系数平方和的算术根
知新探究
【例1】求点P(-1,2)到直线l:3x=2的距离.
解:
方法1:点P(-1,2)到直线l:3x-2=0的距离
方法2:由直线l可得,,
.
∴点P(-1,2)到直线l:3x=2的距离
分析:将直线l的方程写成3x-2=0,再用点到直线的距离公式求解.
直线l有什么特性?
由此你能给出简便解法吗?
.
初试身手
1.求点P(3,-2)到下列直线的距离:
⑴; ⑵y=3; ⑶x=-1.
解:
⑴∵直线可化为3x-4y+1=0,
∴点P(3,-2)到直线的距离
.
⑵点P(3,-2)到直线y=3的距离
.
⑶点P(3,-2)到直线x=-1的距离
.
知新探究
【例2】已知△ABC的三个顶点分别是A(1,3),B(3,1),C(-1,0),求△ABC的面积.
解:
如图,设AB边上的高为h,则
,
|AB|=,
边AB上的高为h就是点C到直线AB的距离.
边AB所在直线l的方程为,
即,
∴点C(-1,0)到x+y-4=0的距离.
因此,.
分析:由三角形面积公式可知,只有利用距离公式求出边AB的长和边AB上的高即可.
你还有其他解法吗?
初试身手
解:
由直线方程的两点式得直线BC的方程为,
即x-2y+3=0,
点A到BC的距离为d,即为BC边上的高,
.
由两点间距离公式得
2.已知点A(-1,3), B(-3,0), C(1,2),求△ABC的面积.
|BC|=.
∴=4.
新知探究
【例3】已知点P(2,-1),求过点P且与原点距离为2的直线l的方程.
当直线l的斜率不存在时,直线l的方程为x=2,符合题意;
当直线l的斜率存在时,设直线l的方程为y+1=k(x-2),
即kx-y-2k-1=0,
,
∴直线l的方程为y+1=(x-2),即3x-4y-10=0.
由点到直线距离公式得,
解:
解得,
故直线l的方程为x=2或3x-4y-10=0.
初试身手
3.求过点M(-2,1),且与A(-1,2),B(3,0)两点距离相等的直线l的方程..
解:
方法1:当直线l斜率不存在时,不存在符合题意的直线.
当直线l斜率存在时,设所求的直线方程为y-1=k(x+2),
即kx-y+2k+1=0,
由题意得
解得k=0或k=.
故所求的直线l方程为y=1或x+2y=0.
初试身手
3.求过点M(-2,1),且与A(-1,2),B(3,0)两点距离相等的直线l的方程..
解:
方法2:由平面几何知识,得l∥AB或l过AB中点.
若l∥AB,
∵kAB=,且直线l过点M(-2,1),
∴直线l方程为x+2y=0
若l过AB的中点N(1,1),又直线l过点M(-2,1),则l的方程为y=1.
故所求的直线l方程为y=1或x+2y=0.
课堂小结
点P(x0,y0)到直线l:Ax+By+C=0的距离:
.
点到直线的距离公式.
应用点到直线的距离公式的关注点:
⑴直线方程应为一般式,若给出其他形式应化为一般式;
⑵直线方程Ax+By+C=0中,A=0或B=0公式也成立;
⑶点P在直线l上时,点到直线的距离为0,公式仍然适用.
作业布置
作业: P77 练习 第2⑵⑶,3题
P79-80 习题2.3 第6,13,14题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
