统计—高一数学北师大版(2019)必修一单元检测卷(B卷)(含解析)
文档属性
| 名称 | 统计—高一数学北师大版(2019)必修一单元检测卷(B卷)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 631.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-07 20:24:52 | ||
图片预览




文档简介
(6)统计—高一数学北师大版(2019)必修一单元检测卷(B卷)
【满分:150分】
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.为了解某地区居民使用手机扫码支付的情况,拟从该地区的居民中抽取部分人员进行调查,事先已了解到该地区老、中、青三个年龄段的人员使用手机扫码支付的情况有较大差异,而男、女使用手机扫码支付的情况差异不大.在下面的抽样方法中,最合理的是( )
A.抽签法 B.按性别分层抽样
C.按年龄段分层抽样 D.随机数法
2.某中学有高中生1800人,初中生1200人,为了解学生课外锻炼情况,用分层随机抽样的方法从学生中抽取一个容量为n的样本.已知从高中生中抽取的人数比从初中生中抽取的人数多24,则( )
A.48 B.72 C.60 D.120
3.某中学高二1班共有50名同学,其中男生30名,女生20名,采用按比例分层随机抽样方法,从全班学生中抽取20人测量其身高(单位:).已知在抽取的样本中,男生的平均身高为,女生的平均身高为,由此估计该班全体学生的平均身高约为( )
A. B. C. D.
4.为调查某地区中学生每天睡眠时间,采用样本量比例分配的分层随机抽样,现抽取初中生800人,其每天睡眠时间均值为9小时,方差为1,抽取高中生1200人,其每天睡眠时间均值为8小时,方差为0.5,则估计该地区中学生每天睡眠时间的方差为( )
A.0.96 B.0.94 C.0.79 D.0.75
5.某农业研究部门在面积相等的100块稻田上种植一种新型水稻,得到各块稻田的亩产量(单位:)并部分整理如下表所示.
亩产
频数 6 12 18 30 24 10
根据表中数据,下列结论正确的是( )
A.100块稻田亩产量的中位数小于
B.100块稻田中亩产量低于的稻田所占比例超过
C.100块稻田亩产量的极差介于到之间
D.100块稻田亩产量的平均值介于到之间
6.已知某样本的容量为50,平均数为70,方差为75.现发现在收集这些数据时,其中的两个数据记录有误,一个错将80记录为60,另一个错将70记录为90.在对错误的数据进行更正后,重新求得样本的平均数为,方差为,则( )
A., B., C., D.,
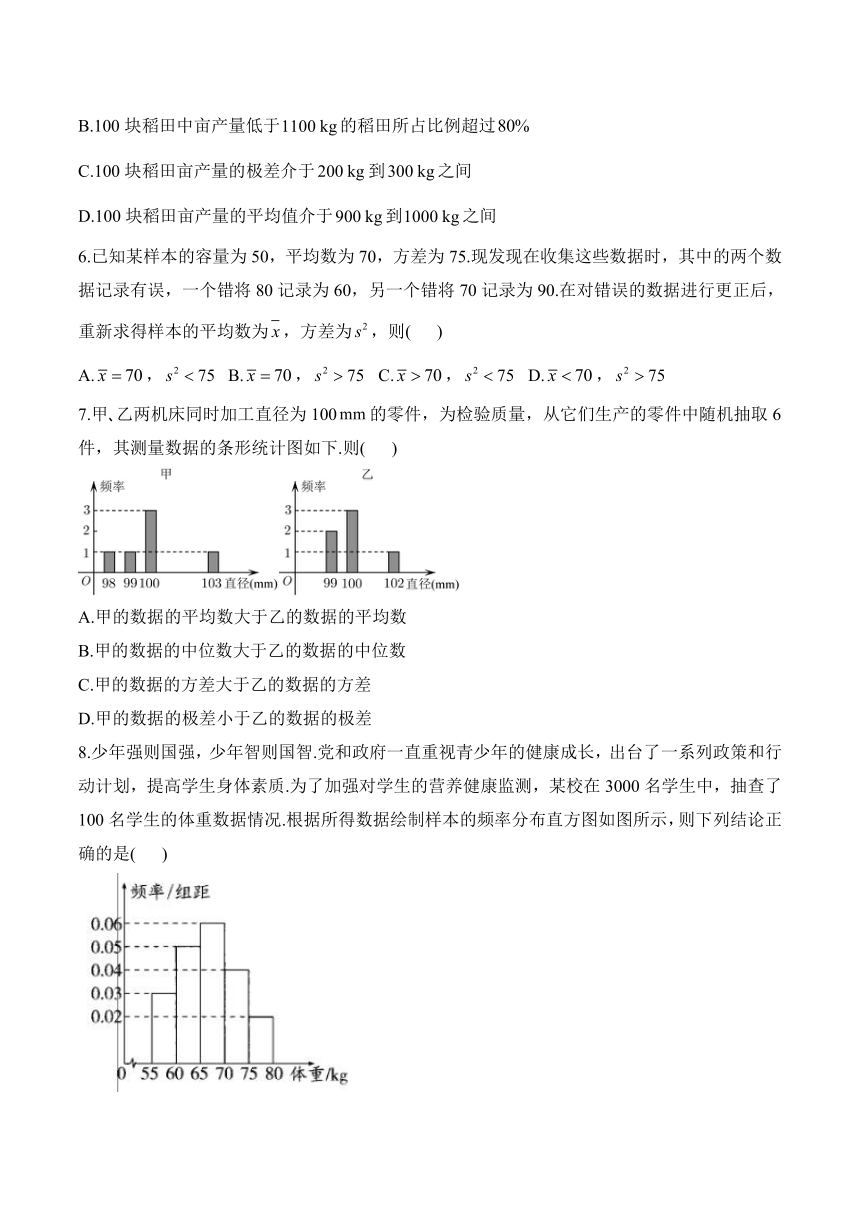
7.甲 乙两机床同时加工直径为100的零件,为检验质量,从它们生产的零件中随机抽取6件,其测量数据的条形统计图如下.则( )
A.甲的数据的平均数大于乙的数据的平均数
B.甲的数据的中位数大于乙的数据的中位数
C.甲的数据的方差大于乙的数据的方差
D.甲的数据的极差小于乙的数据的极差
8.少年强则国强,少年智则国智.党和政府一直重视青少年的健康成长,出台了一系列政策和行动计划,提高学生身体素质.为了加强对学生的营养健康监测,某校在3000名学生中,抽查了100名学生的体重数据情况.根据所得数据绘制样本的频率分布直方图如图所示,则下列结论正确的是( )
A.样本的众数为65
B.样本的第80百分位数为72.5
C.样本的平均数为67.5
D.该校学生中低于65 kg的学生大约为1000人
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.合肥市某中学高一年级学生参加了一次英语口语能力测试(满分10分),其中男生540人,女生360人。现在按性别进行分层,通过分层随机抽样的方法,得到一组测试成绩的样本。样本中有8位女生的测试成绩,分别是6,7,7,7,8,9,10,10,样本中男生测试成绩的平均数为7.5,则( )
A.样本中有12位男生的测试成绩 B.样本中女生测试成绩的第75百分位数是9
C.样本中女生测试成绩的标准差为 D.样本中所有学生测试成绩的平均数为7.75
10.某商户收集并整理了其在2023年1月到8月线上和线下收入的数据,并绘制如图所示的折线图,则下列结论正确的是( )
A.该商户这8个月中,月收入最高的是7月
B.该商户这8个月的线上总收入低于线下总收入
C.该商户这8个月中,线上、线下收入相差最小的是7月
D.该商户这8个月中,月收入不少于17万元的频率是
11.为响应城市倡导的低碳出行,小李上班可以选择公交车、自行车两种交通工具,他分别记录了100次坐公交车和骑车所用时间(单位:分钟),得到下列两个频率分布直方图:
基于以上统计信息,则( )
A.骑车时间的中位数的估计值是22分钟
B.坐公交车时间的40%分位数的估计值是19分钟
C.坐公交车时间的平均数的估计值小于骑车时间的平均数的估计值
D.坐公交车时间的方差的估计值小于骑车时间的方差的估计值
三、填空题:本题共3小题,每小题5分,共15分.
12.某工厂一、二、三、四4个车间共有职工1500人,为了了解职工对工厂某项改革措施的意见,计划从这1500名职工中抽取一个容量为30的样本,考虑采取分层随机抽样的方法.若从一、二、三、四4个车间抽取的人数恰好为4个按照从小到大的顺序排列的连续正整数,则该工厂第四车间的人数为__________.
13.为了解全校学生平均每年阅读多少本书,甲同学抽取了一个容量为20的样本,并算得样本的平均数为5,方差为1;乙同学抽取了一个容量为10的样本,并算得样本的平均数为4,方差为1.若甲、乙两同学抽取的样本合在一起组成一个容量为30的样本,则合在一起后的样本方差为__________.
14.某公司对来应聘的人进行笔试,统计出200名应聘者的笔试成绩,整理得到下表:
组号 1 2 3 4 5 6
成绩分组
累积频率 0.05 0.15 a
注:第n组的累积频率指的是前n组的频率之和.
若公司计划150人进入面试,则估计参加面试的最低分数线为__________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)某大型超市抽查了100天该超市的日纯利润数据,并分成了以下几组(单位:万元):,,,,,.统计结果如下表所示(统计表中每个小组取中间值作为该组数据的替代值):
组别
频数 5 20 30 30 10 5
(1)求这100天该大型超市日纯利润的平均数及中位数;
(2)利用上述样本分布估计总体分布,解决下面问题:该大型超市总经理根据每天的纯利润给员工制定了两种奖励方案:
方案一:记日纯利润为x万元,当时,奖励每位员工40元/天;当时,奖励每位员工80元/天;当时,奖励每位员工120元/天;
方案二:日纯利润低于总体中位数时每名员工发放奖金50元/天,日纯利润不低于总体中位数时每名员工发放80元奖金/天;
“小张恰好为该大型超市的一位员工,则从统计角度看,小张选择哪种奖励方案更有利?
16.(15分)某校从高一年级学生中随机抽取60名学生,将期中考试的数学成绩均为整数分成六组:,,,,,后得到如图所示频率分布直方图.
(1)求a的值;
(2)根据频率分布直方图,求众数和中位数;
(3)用比例分配的分层随机抽样的方法在各分数段的学生中抽取一个容量为20的样本,求在分数段抽取的人数;
17.(15分)出口“新三样”指的是电动载人汽车,锂离子蓄电池和太阳能电池,这些产品在中国外贸出口中扮演着重要角色,成为展现中国制造迈向高端化,智能化,绿色化的崭新名片.某学校组织了400名学生参加新能源知识竞赛,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:,,,,,整理得到频率分布直方图如图所示.
(1)由频率分布直方图估计样本中学生分数的中位数;
(2)已知样本中分数在的学生有5人,试估计总体中分数小于40的人数;
(3)已知样本中男生与女生的比例是3:1,男生样本的平均数为70,方差为10,女生样本的平均数为80,方差为12,请计算出总体的方差.
18.(17分)联合国教科文组织确定每年的4月23日为“世界读书日”,以促进更多的人去阅读,享受阅读的乐趣.为建设读书校园,提升校园的读书氛围,市教育局准备在全市义务教育四年级至九年级学段开展“读书月”活动,活动前,为了解学生的阅读情况,从四年级至九年级在校学生中随机问卷调查了10000人,得到他们在过去一个月中平均每天课外的阅读时间t(单位:分钟),整理得到如右的频率分布直方图,已知这10000人的平均每天课外阅读时间的中位数是31.
(1)求频率分布直方图中m、n的值;
(2)若为整数,将本次调查中平均每天课外阅读时间的学生选为“读书月”活动的宣传大使,教育局准备至少选出1500名“读书月”宣传大使,求的最大值;
(3)为了进一步了解学生的课外阅读习惯受电子产品的影响,由频率分布直方图中平均阅读时间在和两组学生中,按人数比例分配的分层抽样方法抽取了100名学生,已知组的学生平均每天花在电子产品上的时间为30分钟,方差为36,组的学生平均每天花在电子产品上的时间为20分钟,方差为16,求抽取的100名学生每天花在电子产品上的时间的方差.
19.(17分)2024年4月25日,神舟十八号载人飞船顺利发射,本次乘组将首次在空间站实施水生生态项目,即要实现“太空养鱼”,意味着我们有能力在太空构造新的生态环境和生态系统.郑州航天电子技术有限公司为此次任务提供了科技产品和技术服务,该公司为了提高单位职工的工作热情,开展了知识比赛,满分120分,100分及以上为“航天达人”,结果航天达人有t人,这t人按年龄分成了5组,其中第一组:,第二组:,第三组:,第四组,,第五组:,得到的频率分布直方图如下图,已知第一组有10个人.
(1)根据频率分布直方图,估计这t人年龄的第80百分位数;
(2)现从以上各组中用分层随机抽样的方法抽取20人,担任“航天工程”的宣传大使.若第四组宣传大使的年龄的平均数与方差分别为36和,第五组宣传大使的年龄的平均数与方差分别为42和1,据此估计这t人中35~45岁所有人的年龄的平均数和方差.(分层随机抽样中各层抽取的样本量、样本平均数和样本方差分别为:m,,,n,,.记总体的样本平均数为,样本方差为,则,
答案以及解析
1.答案:C
解析:依题意,根据男、女使用手机扫码支付的情况差异不大,老、中、青三个年龄段的人员使用手机扫码支付的情况有较大差异,所以最合理的抽样方法是按年龄段分层随机抽样.故选C.
2.答案:D
解析:由题意可知分层随机抽样按照的比例进行抽取,
则高中生抽取的人数为;
初中生抽取的人数为.
因为从高中生中抽取的人数比从初中生中抽取的人数多24,所以,
解得,故选D.
3.答案:D
解析:因为抽样比例为,则样本中男生有人,女生有人,所以样本的平均身高为,由此估计该班全体学生的平均身高约为.故选D.
4.答案:B
解析:该地区中学生每天睡眠时间的平均数为(小时),该地区中学生每天睡眠时间的方差为.故选B.
5.答案:C
解析:对于A,因为前3组的频率之和,前4组的频率之和,所以100块稻田亩产量的中位数所在的区间为,故A不正确;
对于B,100块稻田中亩产量低于的稻田所占比例为,故B不正确;
对于C,因为,,所以100块稻田亩产量的极差介于至之间,故C正确;
对于D,100块稻田亩产量的平均值为,故D不正确.
综上所述,故选C.
6.答案:A
解析:解析:由题意,可得,设收集的48个准确数据分别记为,,…,,则,
,
所以.故选A.
7.答案:C
解析:由题设,甲数据为,乙数据为,
所以甲的平均数为,
乙的平均数为,
甲乙中位数均为,
甲的方差,乙的方差,
甲极差为,乙极差为,
综上,甲乙平均数、中位数相同,甲的方差大于乙的方差,甲的极差大于乙的极差.
故A、B、D错误,C正确.
故选:C.
8.答案:B
解析:由频率分布直方图可得众数为67.5,A错误;
平均数为,C错误;
因为体重位于,,,的频率分别为0.15,0.25,0.3,0.2,,所以第80百分位数位于区间内,设第80百分位数为x,则,所以,即样本的第80百分位数为72.5,B正确;样本中低于的学生的频率为,所以该校学生中低于的学生大约为(人),D错误.故选B.
9.答案:AC
解析:高一年级男生、女生之比为,由样本中有8位女生的成绩,
则样本中有12位男生的测试成绩,故A正确
由,则样本中女生测试成绩的第75百分位数是第6项与第7项成绩的平均数,
即,故B错误
样本中女生测试成绩的平均数为8,则其方差为,
即标准差为,故C正确
样本中所有学生测试成绩的平均数为,故D错误.
10.答案:ACD
解析:对于A:该商户这8个月中,月收入分别为16万元,13.5万元,16万元,17万元,17万元,16万元,20万元,17.5万元,月收入最高的是7月,A正确;
对于B:该商户这8个月的线上总收入为72万元,线下总收入为61万元,B错误;
对于C:根据折线图可看出该商户这8个月中,线上、线下收入相差最小的是7月,C正确;
对于D:该商户这8个月中,月收入不少于17万元的有4个月,故所求频率为,D正确.
11.答案:BC
解析:对A:设骑车时间的中位数为a,则,解得,故骑车时间的中位数的估计值是21.5分钟,A错误;
对B:设坐公交本时间的分位数为b,则,解得,
故坐公交车时间的分位数的估计值是19分钟,B正确;
对C:坐公交车时间的平均数
,骑车时间的平均数,
,故坐公交车时间的平均数的估计值小于骑车时间的平均数的估计值,C正确;
对D:坐公交车时间的方差,骑车时间的方差,故坐公交车时间的方差的估计值大于骑车时间的方差的估计值,D错误.故选BC.
12.答案:450
解析:设从一、二、三、四4个车间抽取的人数依次为x,,,,则,解得,所以从第四车间抽取9人.
根据分层随机抽样的概念可知,第四车间人数占4个车间总人数的比例为,所以该工厂第四车间有(人).
13.答案:
解析:依题意,合在一起后的样本平均数为,
故合在一起后的样本方差为.
14.答案:65
解析:由各组累积频率为1得,,则.又,设面试的最低分数线为笔试成绩从低到高排列的分位数m,由题表知,笔试成绩分别在与的累积频率分别为0.15,0.35,故,
解得,
从而可估计参加面试的最低分数线为65.
15.答案:(1)平均数为6.85万元,中位数为万元;
(2)方案一.
解析:(1)这100天该大型超市日纯利润的平均数为:
(万元).
前2组频率之和为,前3组频率之和为,
故中位数位于第3组.
设中位数为t,则有,解得,
即这100天该大型超市日纯利润的中位数为万元.
(2)设选择方案一时小张每天的奖金为X元,
则X的可能取值为40,80,120,其对应的概率分别为0.25,0.6,0.15,
所以获得奖金的平均数(元).
设选择方案二时小张每天的奖金为Y元,
则获得奖金的平均数(元).
因为,所以从统计角度看,小张选择方案一更有利.
16.答案:(1);
(2);
(3)11人
解析:(1)由题意可得,
解得,
(2)根据频率分布直方图可知,分数段的频率最高,因此众数为75,.
设中位数为x,则,
解得;
(3)因为总体共60名学生,样本容量为20,因此抽样比为.
又在分数段共有(人),
因此在分数段抽取的人数是(人);
17.答案:(1)72.5
(2)20人
(3)29.25
解析:(1)在频率分布直方图,中位数左边和右边的直方图面积应该相等,
由于,.因此中位数落在之间.
设中位数为x,则有,解得,
所以样本中学生分数的中位数约为72.5.
(2)由频率分布直方图知,
分数在的频率为,
样本中分数在的人数为(人),
样本中分数在的人数为95人,
所以估计总体中分数在的人数为(人),
总体中分数小于40的人数为人;
(3)总样本的均值为,
所以总样本的方差为.
18.答案:(1),;
(2);
(3)
解析:(1),,.
(2)通过直方图可知第85百分位数落在第组,,
解得,因为,所以,
(3)按分层抽样在组抽取40人记为,,,,
则,,
在组抽取60人,记为,,,,同理可得,
平均值为,
抽取的100名学生每天花在电子产品上的时间的方差
.
19.答案:(1)37.5;
(2)年龄的平均数为38,方差约为10
解析:(1)设第80百分位数为a,
,,
a位于第四组:内;
由得:.
(2)由题意得,第四组应抽取人;第五组抽取人,设第四组的宣传使者的年龄分别为,,,,平均数分别为,方差分别为,
设第五组的宣传使者的年龄分别为,,平均数分别为,方差分别为,
设第四组和第五组所有宣传使者的年龄平均数为,方差为.
则,
即第四组和第五组所有宣传使者的年龄平均数为38,
则
.
即第四组和第五组所有宣传使者的年龄方差为10;
据此估计这t人中年龄在岁的所有人的年龄的平均数为38,方差约为10.
【满分:150分】
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.为了解某地区居民使用手机扫码支付的情况,拟从该地区的居民中抽取部分人员进行调查,事先已了解到该地区老、中、青三个年龄段的人员使用手机扫码支付的情况有较大差异,而男、女使用手机扫码支付的情况差异不大.在下面的抽样方法中,最合理的是( )
A.抽签法 B.按性别分层抽样
C.按年龄段分层抽样 D.随机数法
2.某中学有高中生1800人,初中生1200人,为了解学生课外锻炼情况,用分层随机抽样的方法从学生中抽取一个容量为n的样本.已知从高中生中抽取的人数比从初中生中抽取的人数多24,则( )
A.48 B.72 C.60 D.120
3.某中学高二1班共有50名同学,其中男生30名,女生20名,采用按比例分层随机抽样方法,从全班学生中抽取20人测量其身高(单位:).已知在抽取的样本中,男生的平均身高为,女生的平均身高为,由此估计该班全体学生的平均身高约为( )
A. B. C. D.
4.为调查某地区中学生每天睡眠时间,采用样本量比例分配的分层随机抽样,现抽取初中生800人,其每天睡眠时间均值为9小时,方差为1,抽取高中生1200人,其每天睡眠时间均值为8小时,方差为0.5,则估计该地区中学生每天睡眠时间的方差为( )
A.0.96 B.0.94 C.0.79 D.0.75
5.某农业研究部门在面积相等的100块稻田上种植一种新型水稻,得到各块稻田的亩产量(单位:)并部分整理如下表所示.
亩产
频数 6 12 18 30 24 10
根据表中数据,下列结论正确的是( )
A.100块稻田亩产量的中位数小于
B.100块稻田中亩产量低于的稻田所占比例超过
C.100块稻田亩产量的极差介于到之间
D.100块稻田亩产量的平均值介于到之间
6.已知某样本的容量为50,平均数为70,方差为75.现发现在收集这些数据时,其中的两个数据记录有误,一个错将80记录为60,另一个错将70记录为90.在对错误的数据进行更正后,重新求得样本的平均数为,方差为,则( )
A., B., C., D.,
7.甲 乙两机床同时加工直径为100的零件,为检验质量,从它们生产的零件中随机抽取6件,其测量数据的条形统计图如下.则( )
A.甲的数据的平均数大于乙的数据的平均数
B.甲的数据的中位数大于乙的数据的中位数
C.甲的数据的方差大于乙的数据的方差
D.甲的数据的极差小于乙的数据的极差
8.少年强则国强,少年智则国智.党和政府一直重视青少年的健康成长,出台了一系列政策和行动计划,提高学生身体素质.为了加强对学生的营养健康监测,某校在3000名学生中,抽查了100名学生的体重数据情况.根据所得数据绘制样本的频率分布直方图如图所示,则下列结论正确的是( )
A.样本的众数为65
B.样本的第80百分位数为72.5
C.样本的平均数为67.5
D.该校学生中低于65 kg的学生大约为1000人
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.合肥市某中学高一年级学生参加了一次英语口语能力测试(满分10分),其中男生540人,女生360人。现在按性别进行分层,通过分层随机抽样的方法,得到一组测试成绩的样本。样本中有8位女生的测试成绩,分别是6,7,7,7,8,9,10,10,样本中男生测试成绩的平均数为7.5,则( )
A.样本中有12位男生的测试成绩 B.样本中女生测试成绩的第75百分位数是9
C.样本中女生测试成绩的标准差为 D.样本中所有学生测试成绩的平均数为7.75
10.某商户收集并整理了其在2023年1月到8月线上和线下收入的数据,并绘制如图所示的折线图,则下列结论正确的是( )
A.该商户这8个月中,月收入最高的是7月
B.该商户这8个月的线上总收入低于线下总收入
C.该商户这8个月中,线上、线下收入相差最小的是7月
D.该商户这8个月中,月收入不少于17万元的频率是
11.为响应城市倡导的低碳出行,小李上班可以选择公交车、自行车两种交通工具,他分别记录了100次坐公交车和骑车所用时间(单位:分钟),得到下列两个频率分布直方图:
基于以上统计信息,则( )
A.骑车时间的中位数的估计值是22分钟
B.坐公交车时间的40%分位数的估计值是19分钟
C.坐公交车时间的平均数的估计值小于骑车时间的平均数的估计值
D.坐公交车时间的方差的估计值小于骑车时间的方差的估计值
三、填空题:本题共3小题,每小题5分,共15分.
12.某工厂一、二、三、四4个车间共有职工1500人,为了了解职工对工厂某项改革措施的意见,计划从这1500名职工中抽取一个容量为30的样本,考虑采取分层随机抽样的方法.若从一、二、三、四4个车间抽取的人数恰好为4个按照从小到大的顺序排列的连续正整数,则该工厂第四车间的人数为__________.
13.为了解全校学生平均每年阅读多少本书,甲同学抽取了一个容量为20的样本,并算得样本的平均数为5,方差为1;乙同学抽取了一个容量为10的样本,并算得样本的平均数为4,方差为1.若甲、乙两同学抽取的样本合在一起组成一个容量为30的样本,则合在一起后的样本方差为__________.
14.某公司对来应聘的人进行笔试,统计出200名应聘者的笔试成绩,整理得到下表:
组号 1 2 3 4 5 6
成绩分组
累积频率 0.05 0.15 a
注:第n组的累积频率指的是前n组的频率之和.
若公司计划150人进入面试,则估计参加面试的最低分数线为__________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)某大型超市抽查了100天该超市的日纯利润数据,并分成了以下几组(单位:万元):,,,,,.统计结果如下表所示(统计表中每个小组取中间值作为该组数据的替代值):
组别
频数 5 20 30 30 10 5
(1)求这100天该大型超市日纯利润的平均数及中位数;
(2)利用上述样本分布估计总体分布,解决下面问题:该大型超市总经理根据每天的纯利润给员工制定了两种奖励方案:
方案一:记日纯利润为x万元,当时,奖励每位员工40元/天;当时,奖励每位员工80元/天;当时,奖励每位员工120元/天;
方案二:日纯利润低于总体中位数时每名员工发放奖金50元/天,日纯利润不低于总体中位数时每名员工发放80元奖金/天;
“小张恰好为该大型超市的一位员工,则从统计角度看,小张选择哪种奖励方案更有利?
16.(15分)某校从高一年级学生中随机抽取60名学生,将期中考试的数学成绩均为整数分成六组:,,,,,后得到如图所示频率分布直方图.
(1)求a的值;
(2)根据频率分布直方图,求众数和中位数;
(3)用比例分配的分层随机抽样的方法在各分数段的学生中抽取一个容量为20的样本,求在分数段抽取的人数;
17.(15分)出口“新三样”指的是电动载人汽车,锂离子蓄电池和太阳能电池,这些产品在中国外贸出口中扮演着重要角色,成为展现中国制造迈向高端化,智能化,绿色化的崭新名片.某学校组织了400名学生参加新能源知识竞赛,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:,,,,,整理得到频率分布直方图如图所示.
(1)由频率分布直方图估计样本中学生分数的中位数;
(2)已知样本中分数在的学生有5人,试估计总体中分数小于40的人数;
(3)已知样本中男生与女生的比例是3:1,男生样本的平均数为70,方差为10,女生样本的平均数为80,方差为12,请计算出总体的方差.
18.(17分)联合国教科文组织确定每年的4月23日为“世界读书日”,以促进更多的人去阅读,享受阅读的乐趣.为建设读书校园,提升校园的读书氛围,市教育局准备在全市义务教育四年级至九年级学段开展“读书月”活动,活动前,为了解学生的阅读情况,从四年级至九年级在校学生中随机问卷调查了10000人,得到他们在过去一个月中平均每天课外的阅读时间t(单位:分钟),整理得到如右的频率分布直方图,已知这10000人的平均每天课外阅读时间的中位数是31.
(1)求频率分布直方图中m、n的值;
(2)若为整数,将本次调查中平均每天课外阅读时间的学生选为“读书月”活动的宣传大使,教育局准备至少选出1500名“读书月”宣传大使,求的最大值;
(3)为了进一步了解学生的课外阅读习惯受电子产品的影响,由频率分布直方图中平均阅读时间在和两组学生中,按人数比例分配的分层抽样方法抽取了100名学生,已知组的学生平均每天花在电子产品上的时间为30分钟,方差为36,组的学生平均每天花在电子产品上的时间为20分钟,方差为16,求抽取的100名学生每天花在电子产品上的时间的方差.
19.(17分)2024年4月25日,神舟十八号载人飞船顺利发射,本次乘组将首次在空间站实施水生生态项目,即要实现“太空养鱼”,意味着我们有能力在太空构造新的生态环境和生态系统.郑州航天电子技术有限公司为此次任务提供了科技产品和技术服务,该公司为了提高单位职工的工作热情,开展了知识比赛,满分120分,100分及以上为“航天达人”,结果航天达人有t人,这t人按年龄分成了5组,其中第一组:,第二组:,第三组:,第四组,,第五组:,得到的频率分布直方图如下图,已知第一组有10个人.
(1)根据频率分布直方图,估计这t人年龄的第80百分位数;
(2)现从以上各组中用分层随机抽样的方法抽取20人,担任“航天工程”的宣传大使.若第四组宣传大使的年龄的平均数与方差分别为36和,第五组宣传大使的年龄的平均数与方差分别为42和1,据此估计这t人中35~45岁所有人的年龄的平均数和方差.(分层随机抽样中各层抽取的样本量、样本平均数和样本方差分别为:m,,,n,,.记总体的样本平均数为,样本方差为,则,
答案以及解析
1.答案:C
解析:依题意,根据男、女使用手机扫码支付的情况差异不大,老、中、青三个年龄段的人员使用手机扫码支付的情况有较大差异,所以最合理的抽样方法是按年龄段分层随机抽样.故选C.
2.答案:D
解析:由题意可知分层随机抽样按照的比例进行抽取,
则高中生抽取的人数为;
初中生抽取的人数为.
因为从高中生中抽取的人数比从初中生中抽取的人数多24,所以,
解得,故选D.
3.答案:D
解析:因为抽样比例为,则样本中男生有人,女生有人,所以样本的平均身高为,由此估计该班全体学生的平均身高约为.故选D.
4.答案:B
解析:该地区中学生每天睡眠时间的平均数为(小时),该地区中学生每天睡眠时间的方差为.故选B.
5.答案:C
解析:对于A,因为前3组的频率之和,前4组的频率之和,所以100块稻田亩产量的中位数所在的区间为,故A不正确;
对于B,100块稻田中亩产量低于的稻田所占比例为,故B不正确;
对于C,因为,,所以100块稻田亩产量的极差介于至之间,故C正确;
对于D,100块稻田亩产量的平均值为,故D不正确.
综上所述,故选C.
6.答案:A
解析:解析:由题意,可得,设收集的48个准确数据分别记为,,…,,则,
,
所以.故选A.
7.答案:C
解析:由题设,甲数据为,乙数据为,
所以甲的平均数为,
乙的平均数为,
甲乙中位数均为,
甲的方差,乙的方差,
甲极差为,乙极差为,
综上,甲乙平均数、中位数相同,甲的方差大于乙的方差,甲的极差大于乙的极差.
故A、B、D错误,C正确.
故选:C.
8.答案:B
解析:由频率分布直方图可得众数为67.5,A错误;
平均数为,C错误;
因为体重位于,,,的频率分别为0.15,0.25,0.3,0.2,,所以第80百分位数位于区间内,设第80百分位数为x,则,所以,即样本的第80百分位数为72.5,B正确;样本中低于的学生的频率为,所以该校学生中低于的学生大约为(人),D错误.故选B.
9.答案:AC
解析:高一年级男生、女生之比为,由样本中有8位女生的成绩,
则样本中有12位男生的测试成绩,故A正确
由,则样本中女生测试成绩的第75百分位数是第6项与第7项成绩的平均数,
即,故B错误
样本中女生测试成绩的平均数为8,则其方差为,
即标准差为,故C正确
样本中所有学生测试成绩的平均数为,故D错误.
10.答案:ACD
解析:对于A:该商户这8个月中,月收入分别为16万元,13.5万元,16万元,17万元,17万元,16万元,20万元,17.5万元,月收入最高的是7月,A正确;
对于B:该商户这8个月的线上总收入为72万元,线下总收入为61万元,B错误;
对于C:根据折线图可看出该商户这8个月中,线上、线下收入相差最小的是7月,C正确;
对于D:该商户这8个月中,月收入不少于17万元的有4个月,故所求频率为,D正确.
11.答案:BC
解析:对A:设骑车时间的中位数为a,则,解得,故骑车时间的中位数的估计值是21.5分钟,A错误;
对B:设坐公交本时间的分位数为b,则,解得,
故坐公交车时间的分位数的估计值是19分钟,B正确;
对C:坐公交车时间的平均数
,骑车时间的平均数,
,故坐公交车时间的平均数的估计值小于骑车时间的平均数的估计值,C正确;
对D:坐公交车时间的方差,骑车时间的方差,故坐公交车时间的方差的估计值大于骑车时间的方差的估计值,D错误.故选BC.
12.答案:450
解析:设从一、二、三、四4个车间抽取的人数依次为x,,,,则,解得,所以从第四车间抽取9人.
根据分层随机抽样的概念可知,第四车间人数占4个车间总人数的比例为,所以该工厂第四车间有(人).
13.答案:
解析:依题意,合在一起后的样本平均数为,
故合在一起后的样本方差为.
14.答案:65
解析:由各组累积频率为1得,,则.又,设面试的最低分数线为笔试成绩从低到高排列的分位数m,由题表知,笔试成绩分别在与的累积频率分别为0.15,0.35,故,
解得,
从而可估计参加面试的最低分数线为65.
15.答案:(1)平均数为6.85万元,中位数为万元;
(2)方案一.
解析:(1)这100天该大型超市日纯利润的平均数为:
(万元).
前2组频率之和为,前3组频率之和为,
故中位数位于第3组.
设中位数为t,则有,解得,
即这100天该大型超市日纯利润的中位数为万元.
(2)设选择方案一时小张每天的奖金为X元,
则X的可能取值为40,80,120,其对应的概率分别为0.25,0.6,0.15,
所以获得奖金的平均数(元).
设选择方案二时小张每天的奖金为Y元,
则获得奖金的平均数(元).
因为,所以从统计角度看,小张选择方案一更有利.
16.答案:(1);
(2);
(3)11人
解析:(1)由题意可得,
解得,
(2)根据频率分布直方图可知,分数段的频率最高,因此众数为75,.
设中位数为x,则,
解得;
(3)因为总体共60名学生,样本容量为20,因此抽样比为.
又在分数段共有(人),
因此在分数段抽取的人数是(人);
17.答案:(1)72.5
(2)20人
(3)29.25
解析:(1)在频率分布直方图,中位数左边和右边的直方图面积应该相等,
由于,.因此中位数落在之间.
设中位数为x,则有,解得,
所以样本中学生分数的中位数约为72.5.
(2)由频率分布直方图知,
分数在的频率为,
样本中分数在的人数为(人),
样本中分数在的人数为95人,
所以估计总体中分数在的人数为(人),
总体中分数小于40的人数为人;
(3)总样本的均值为,
所以总样本的方差为.
18.答案:(1),;
(2);
(3)
解析:(1),,.
(2)通过直方图可知第85百分位数落在第组,,
解得,因为,所以,
(3)按分层抽样在组抽取40人记为,,,,
则,,
在组抽取60人,记为,,,,同理可得,
平均值为,
抽取的100名学生每天花在电子产品上的时间的方差
.
19.答案:(1)37.5;
(2)年龄的平均数为38,方差约为10
解析:(1)设第80百分位数为a,
,,
a位于第四组:内;
由得:.
(2)由题意得,第四组应抽取人;第五组抽取人,设第四组的宣传使者的年龄分别为,,,,平均数分别为,方差分别为,
设第五组的宣传使者的年龄分别为,,平均数分别为,方差分别为,
设第四组和第五组所有宣传使者的年龄平均数为,方差为.
则,
即第四组和第五组所有宣传使者的年龄平均数为38,
则
.
即第四组和第五组所有宣传使者的年龄方差为10;
据此估计这t人中年龄在岁的所有人的年龄的平均数为38,方差约为10.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
