统计—高一数学北师大版(2019)必修一单元检测卷(A卷)(含解析)
文档属性
| 名称 | 统计—高一数学北师大版(2019)必修一单元检测卷(A卷)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 698.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-07 20:25:45 | ||
图片预览



文档简介
(6)统计—高一数学北师大版(2019)必修一单元检测卷(A卷)
【满分:150分】
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列各项调查中你认为合理的有( )
①为了了解全校同学喜欢课程情况,对某班男同学进行抽样调查
②“神舟十四号”飞船发射前,采用抽样调查的方式检查其各零部件的合格情况
③采用抽样调查的方式了解国内外观众对电影《流浪地球》的观影感受
④为调查我市居民对“垃圾分类”有关内容的了解程度,将要调查的问题放到某网站上,这样大部分上网的人就可以看到调查问题并及时反馈
A.0个 B.1个 C.2个 D.3个
2.随机抽查了某校100名高三学生的视力情况,得到的频率分布直方图如图所示,由于不慎将部分数据丢失,但知道后5组的频数和为64,设视力在4.6到4.8之间的学生人数为a,各组中频率最大的为0.34,则a的值为( )
A.64 B.54 C.48 D.27
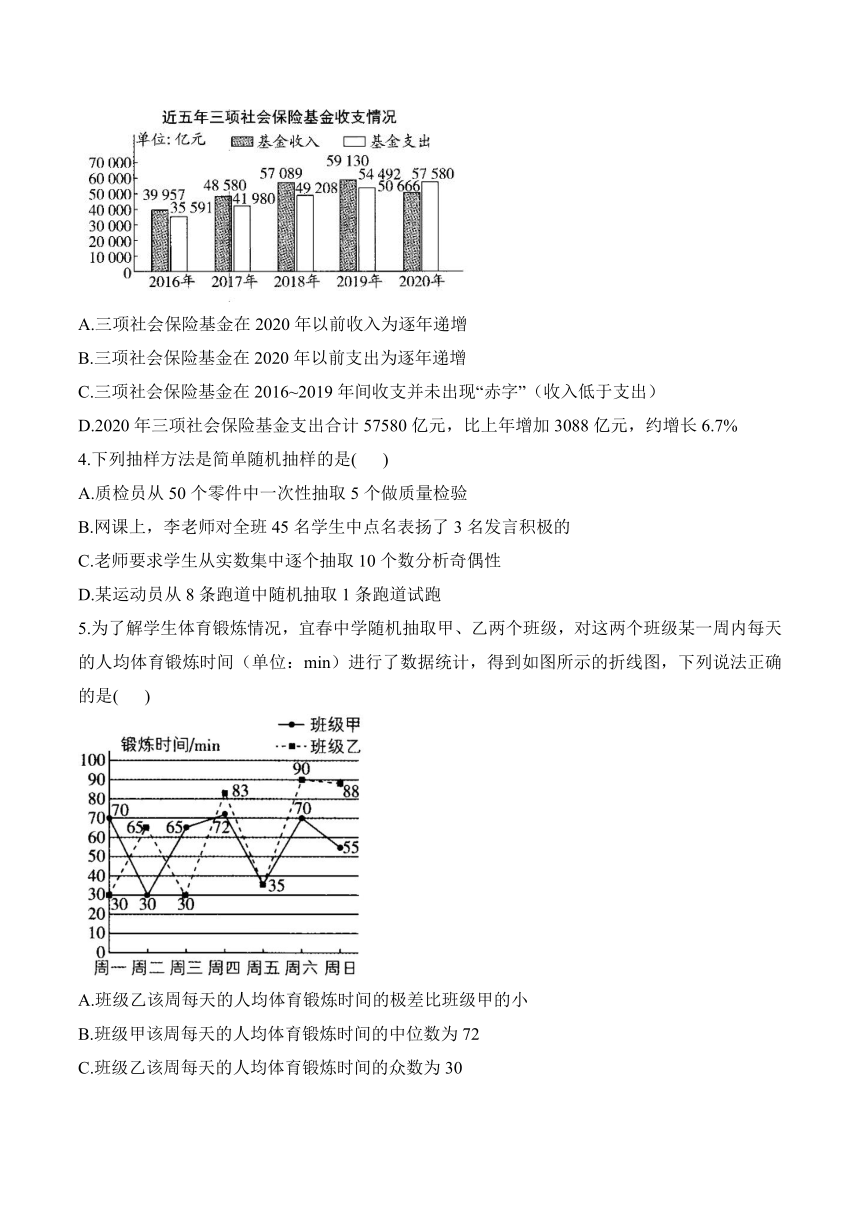
3.“社保”已经走入了我们的生活,它包括养老保险、医疗保险、失业保险、工伤保险、生育保险,全年支出最重要的三项分别为养老保险、失业保险、工伤保险,下图是近五年三项社会保险基金的收支情况,下列说法中错误的是( )
A.三项社会保险基金在2020年以前收入为逐年递增
B.三项社会保险基金在2020年以前支出为逐年递增
C.三项社会保险基金在2016~2019年间收支并未出现“赤字”(收入低于支出)
D.2020年三项社会保险基金支出合计57580亿元,比上年增加3088亿元,约增长6.7%
4.下列抽样方法是简单随机抽样的是( )
A.质检员从50个零件中一次性抽取5个做质量检验
B.网课上,李老师对全班45名学生中点名表扬了3名发言积极的
C.老师要求学生从实数集中逐个抽取10个数分析奇偶性
D.某运动员从8条跑道中随机抽取1条跑道试跑
5.为了解学生体育锻炼情况,宜春中学随机抽取甲、乙两个班级,对这两个班级某一周内每天的人均体育锻炼时间(单位:min)进行了数据统计,得到如图所示的折线图,下列说法正确的是( )
A.班级乙该周每天的人均体育锻炼时间的极差比班级甲的小
B.班级甲该周每天的人均体育锻炼时间的中位数为72
C.班级乙该周每天的人均体育锻炼时间的众数为30
D.班级甲该周每天的人均体育锻炼时间的平均数比班级乙的大
6.已知某7个数的平均数为3,方差为3,现加入一个新数据3,此时这8个数的平均数为,标准差为s,则( )
A., B., C., D.,
7.某零件加工厂认定工人通过试用期的方法为:随机选取试用期中的5天,再从每天生产的零件中分别随机抽取25件,要求每天合格品均不低于22件.若甲、乙、丙三人在其5天抽检样本中的合格品件数统计如下,甲:中位数为24,极差不超过2;乙:平均数为23,方差不超过1;丙:众数为23,方差不超过1,则一定能通过试用期的有( )
A.甲、乙 B.甲、丙 C.乙、丙 D.甲、乙、丙
8.某校开展“正心立德,劳动树人”主题教育活动,对参赛的100名学生的劳动作品的得分情况进行统计,并绘制了如图所示的频率分布直方图(每组为左闭右开区间),根据图中信息,下列结论错误的是( )
A.图中的x值为0.020
B.得分在80分及以上的人数为40
C.这组数据平均数的估计值为77
D.这组数据第80百分位数的估计值为85
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列命题是真命题的有( )
A.分层抽样调查后的样本中甲、乙、丙三种个体的比例为,如果抽取的甲个体数为9,则样本容量为30
B.某一组样本数据为125,120,122,105,130,114,116,95,120,134,则样本数据落在区间内的频率为0.4
C.甲、乙两队队员体重的平均数分别为60,68,人数之比为,则甲、乙两队全部队员体重的平均数为67
D.一组数6,5,4,3,3,3,2,2,2,1的85%分位数为5
10.某校为了解学生对食堂的满意程度,设计了一份调查问卷,从该校高中生中随机抽取部分学生参加测试,记录了他们的分数,将收集到的学生测试分数按照,,,,,,分组,画出频率分布直方图,已知随机抽取的学生测试分数不低于80分的学生有27人,则以下结论中正确的是( )
A.此次测试众数的估计值为85
B.此次测试分数在的学生人数为6
C.随机抽取的学生测试分数的第55百分位数约为80
D.平均数m在中位数n右侧
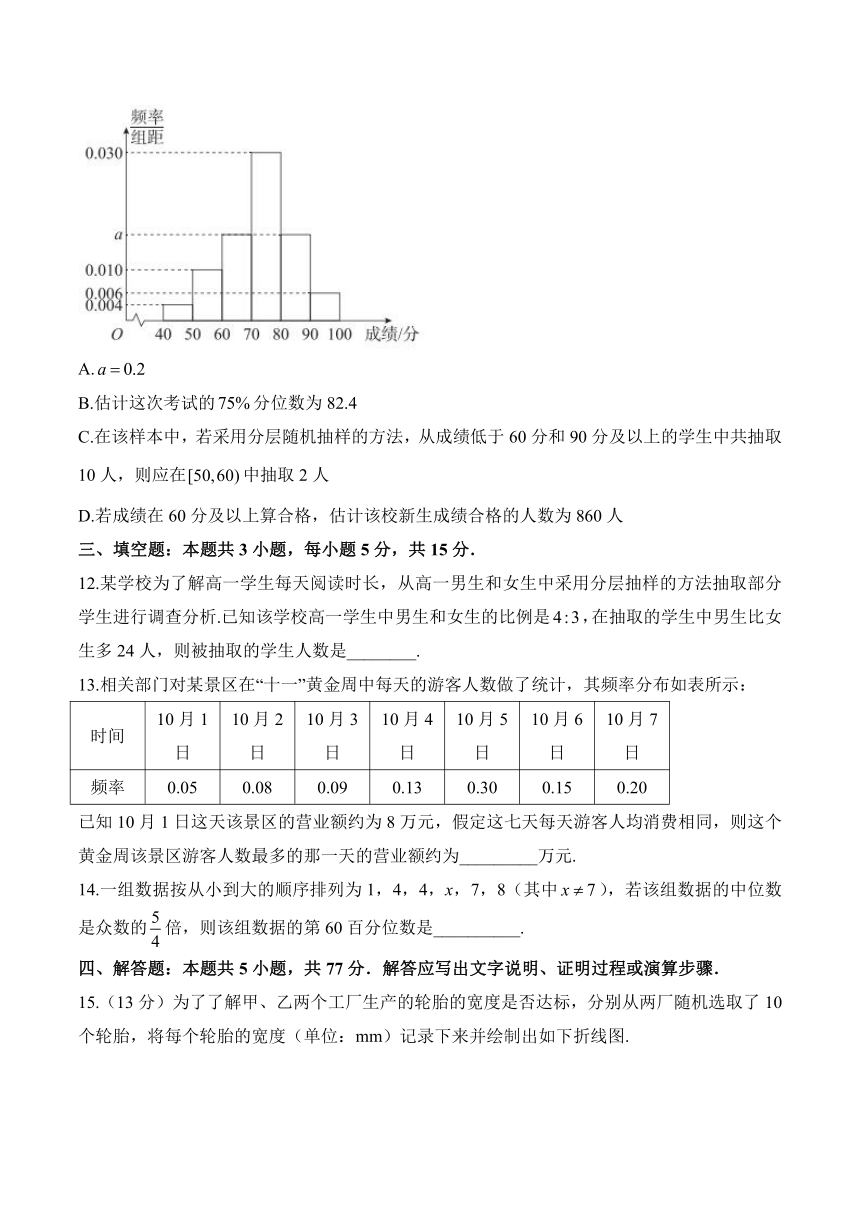
11.某校开学初组织新生进行数学摸底测试,现从1000名考生中,随机抽取200人的成绩(满分为100分)作为样本,得到成绩的频率分布直方图如图所示,其中样本数据分组区间为,,,,,.则下列说法正确的是( )
A.
B.估计这次考试的分位数为82.4
C.在该样本中,若采用分层随机抽样的方法,从成绩低于60分和90分及以上的学生中共抽取10人,则应在中抽取2人
D.若成绩在60分及以上算合格,估计该校新生成绩合格的人数为860人
三、填空题:本题共3小题,每小题5分,共15分.
12.某学校为了解高一学生每天阅读时长,从高一男生和女生中采用分层抽样的方法抽取部分学生进行调查分析.已知该学校高一学生中男生和女生的比例是,在抽取的学生中男生比女生多24人,则被抽取的学生人数是________.
13.相关部门对某景区在“十一”黄金周中每天的游客人数做了统计,其频率分布如表所示:
时间 10月1日 10月2日 10月3日 10月4日 10月5日 10月6日 10月7日
频率 0.05 0.08 0.09 0.13 0.30 0.15 0.20
已知10月1日这天该景区的营业额约为8万元,假定这七天每天游客人均消费相同,则这个黄金周该景区游客人数最多的那一天的营业额约为_________万元.
14.一组数据按从小到大的顺序排列为1,4,4,x,7,8(其中),若该组数据的中位数是众数的倍,则该组数据的第60百分位数是__________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)为了了解甲、乙两个工厂生产的轮胎的宽度是否达标,分别从两厂随机选取了10个轮胎,将每个轮胎的宽度(单位:mm)记录下来并绘制出如下折线图.
(1)分别计算甲、乙两厂提供的10个轮胎宽度的平均数.
(2)若轮胎的宽度在内,则称这个轮胎是标准轮胎.
(ⅰ)若从甲厂提供的10个轮胎中随机选取1个,求所选的轮胎是标准轮胎的概率;
(ⅱ)试比较甲、乙两厂分别提供的10个轮胎中所有标准轮胎宽度的方差的大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个厂的轮胎相对更好.
16.(15分)已知某科技公司的某型号芯片的各项指标经过全面检测后,分为I级和Ⅱ级,两种品级芯片的某项指标的频率分布直方图如图所示:
若只利用该指标制定一个标准,需要确定临界值K,将该指标大于K的产品应用于A型手机,小于或等于K的产品应用于B型手机.假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.
(1)若临界值,请估计该公司生产的1000个该型号芯片I级品和1000个Ⅱ级品中应用于A型手机的芯片个数;
(2)设且,现有足够多的芯片I级品 Ⅱ级品,分别应用于A型手机 B型手机各1万部的生产:
方案一:直接将该芯片I级品应用于A型手机,其中该指标小于等于临界值K的芯片会导致芯片生产商每部手机损失800元;直接将该芯片Ⅱ级品应用于B型手机,其中该指标大于临界值K的芯片,会导致芯片生产商每部手机损失400元;
方案二:重新检测芯片I级品,Ⅱ级品的该项指标,并按规定正确应用于手机型号,会避免方案一的损失费用,但检测费用共需要130万元;
请求出按方案一,芯片生产商损失费用的估计值(单位:万元)的表达式,并从芯片生产商的成本考虑,选择合理的方案.
17.(15分)某公司为了解员工对食堂的满意程度,随机抽取了200名员工做了一次问卷调查,要求员工对食堂的满意程度进行打分,所得分数均在内,现将所得数据分成6组:,,,,,,并得到如图所示的频率分布直方图.
(1)求a的值,并估计这200名员工所得分数的平均数(同一组中的数据用该组区间的中点值代表);
(2)求这200名员工所得分数的中位数(精确到0.1);
(3)现从,,这三组中用比例分配的分层随机抽样的方法抽取24人,求这组中抽取的人数.
18.(17分)2023年秋末冬初,呼和浩特市发生了流感疾病.为了彻底击败病毒,人们更加讲究卫生讲究环保.某学校开展组织学生参加线上环保知识竞赛活动,现从中抽取200名学生,记录他们的首轮竞赛成绩并作出如图所示的频率直方图,根据图形,请回答下列问题:
(1)若从成绩低于60分的同学中按分层抽样方法抽取5人成绩,求5人中成绩低于50分的人数;
(2)以样本估计总体,利用组中值估计该校学生首轮竞赛成绩的平均数;
(3)首轮竞赛成绩位列前的学生入围第二轮的复赛,请根据图中信息,估计入围复赛的成绩(记为K).
19.(17分)2024年5月22日至5月28日是第二届全国城市生活垃圾分类宣传周,本次宣传周的主题为“践行新时尚分类志愿行”.阜阳三中高一年级举行了一次“垃圾分类知识竞赛”,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩x(单位:分,得分取正整数,满分为100分)作为样本进行统计将成绩进行整理后,分为五组(,,,,),其中第1组频数的平方等于第2组、第4组频数之积,请根据下面尚未完成的频率分布直方图(如图所示)解决下列问题:
(1)求a,b的值;
(2)若根据这次成绩,学校准备淘汰的同学,仅留的同学进入下一轮竞赛请问晋级分数线划为多少合理
(3)某老师在此次竞赛成绩中抽取了10名学生的分数:,,,…,,已知这10个分数的平均数,标准差,若剔除其中的95和85这两个分数,求剩余8个分数的平均数与方差.
答案以及解析
1.答案:B
解析:①了解全校同学喜欢课程情况,应在各班进行抽样,同时不能仅限男同学,不合理;
②“神舟十四号”飞船发射前,应采用全面调查检查其各零部件的合格情况,不合理;
③了解国内外观众对电影《流浪地球》的观影感受,采用抽样调查,合理;
④对“垃圾分类”有关内容的了解程度,问题放到某网站上,受调查人群有局限,不合理.
故选:B.
2.答案:B
解析:由题意知,前两组的频数之和为,第四组的频数为,后五组的频数之和为64,所以前二组的频数之和为,故第三组的频数为,因此.故选B.
3.答案:D
解析:由条形图可知,三项社会保险基金在2020年以前收入为逐年递增的,故A正确;
三项社会保险基金在2020年以前支出为逐年递增的,故B正确;
三项社会保险基金在2016~2019年间收支并未出现“赤字”,故C正确;
2020年三项社会保险基金支出合计57580亿元,比上年增加3088亿元,约增长,故D错误.故选D.
4.答案:D
解析:选项A,一次性抽取不是逐个不放回地抽取,不符合简单随机抽样的要求,故A错误;
选项B,老师表扬的是发言积极的,对每一个个体而言,不具备“等可能性:”,故B错误;
选项C,因为总体容量是无限的,不符合简单随机抽样的要求,故C错误;
选项D,8条跑道,抽取1条,总体有限,每个个体被抽到的机会均等,是简单随机抽样,故D正确.故选D.
5.答案:C
解析:由题意可知,班级甲的数据按从小到大的顺序排列得30,35,55,65,70,70,72;
班级乙的数据按从小到大的顺序排列得30,30,35,65,83,88,90.
对于选项A:班级甲的极差为,班级乙的极差为,
所以班级乙该周每天的人均体育锻炼时间的极差比班级甲的大,故A错误;
对于选项B:班级甲该周每天的人均体育锻炼时间的中位数为65,故B错误;
对于选项C:班级乙该周每天的人均体育锻炼时间的众数为30,故C正确;
对于选项D:班级甲的平均数,班级乙的平均数,所以班级甲该周每天的人均体育锻炼时间的平均数比班级乙的小,故D错误.故选C.
6.答案:B
解析:某7个数的平均数为3,方差为3,现加入一个新数据3,此时这8个数的平均数为,标准差为s,方差为,,,.故选B.
7.答案:A
解析:对于甲:由甲的统计数据可知,甲至少有3天的合格品数不低于24,最低合格品数不低于2,所以甲一定能通过;
对于乙:设乙每天的合格品件数为,,则,
即.若乙有不止一天的合格品数低于21,,不合题意;
若乙只有一天的合格品数低于22,不妨取,,因为平均数为23,则至少有一天的合格品数为25或至少有两天的合格品数为24,无论哪种情况,都可以得到,不合题意,所以乙的每一天的合格品数都不低于22,乙一定能通过;
对于丙:若丙的合格品数为21,22,23,23,23,则丙的众数为23,方差为0.64,符合丙的统计数据,但丙不能通过;
所以甲、乙一定能通过,A正确;
故选:A.
8.答案:D
解析:由频率之和为1得,解得,A正确,不符合题意;得分在80分及以上的人数为,B正确,不符合题意;因为,所以C正确,不符合题意;因为,,所以这组数据第80百分位数的估计值落在区间内,,故这组数据第80百分位数的估计值不为85,D错误,符合题意.故选D.
9.答案:BD
解析:对于选项A:根据样本的抽样比等于各层的抽样比,得样本容量为,故选项A为假命题;
对于选项B:样本数据落在区间内的有120,122,116,120,共4个,所以样本数据落在区间内的频率为,故选项B为真命题;
对于选项C:甲、乙两队的人数之比为,则甲队队员在所有队员中所占比例为,乙队队员在所有队员中所占比例为,则甲、乙两队全部队员体重的平均数为,故选项C为假命题;
对于选项D:将该组数据从小到大排列为1,2,2,2,3,3,3,4,5,6,由,则该组数据的分位数是第9个数,该数为5,故选项D为真命题.
10.答案:ABC
解析:由直方图可知此次测试众数的估计值为85,故A正确;因为不低于80分的学生的频率为,所以该校高中生中随机抽取的学生人数为,所以此次测试分数在的学生人数为,故B正确;因为,所以随机抽取的学生测试分数的第55百分位数约为80,故C正确;由直方图在左边“拖尾”可知平均数小于中位数,即平均数m在中位数n左侧,故D错误.故选ABC.
11.答案:BD
解析:对于A:由得,故A错误;
对于B:成绩在区间所占的频率为,成绩在区间所占的频率为,故分位数所在区间为,设分位数为x,则,解得,故B正确;
对于C:低于60分和90分及以上的学生占的频率之和为,成绩在占的频率为,故按分层抽样,应在中抽取的人数为人,故C错误;
对于D:估计该校新生成绩在60以下的人数为,故估计该校新生成绩合格的人数为人,故D正确.故选BD.
12.答案:168
解析:设抽取的学生中男生人数为a,女生人数为b,则,且,解得,,则被抽取的学生人数是.故答案为168.
13.答案:48
解析:设游客人数最多的那一天的营业额约为x万元.由,解得.故游客人数最多的那一天的营业额约为48万元.
14.答案:6
解析:由题意知,众数是4,则中位数为,则,解得,又,则第60百分位数是6.
故答案为:6.
15.答案:(1);
(2)(ⅰ)
(ⅱ)乙厂的轮胎相对更好
解析:(1)甲厂提供的10个轮胎宽度的平均数
.
乙厂提供的10个轮胎宽度的平均数
.
(2)甲厂提供的这10个轮胎的宽度在内的数据为195,194,196,194,196,195.
(ⅰ)所选的轮胎是标准轮胎的概率.
(ⅱ)计算得甲厂提供的10个轮胎中标准轮胎宽度的平均数为195,方差为.
乙厂提供的这10个轮胎的宽度在内的数据为195,196,195,194,195,195,计算得平均数为195,方差为.
由样本估计总体,两厂标准轮胎宽度的平均数相等,但乙的方差较小,所以乙厂的轮胎相对更好.
16.答案:(1)1030;
(2),应选择方案二
解析:(1)临界值时,I级品中该指标大于60的频率为,
Ⅱ级品中该指标大于60的频率为0.1
故该公司生产的1000个该型号芯片I级品和1000个Ⅱ级品中应用于A型手机的芯片个数估计为:
(2)当临界值时,若采用方案一:
I级品中该指标小于或等于临界值K的概率为,可以估计10000部A型手机中有部手机芯片应用错误;
Ⅱ级品中该指标大于临界值K的概率为,
可以估计10000部B型手机中有部手机芯片应用错误;
故可以估计芯片生产商的损失费用
,
又采用方案二需要检测费用共130万元
故从芯片生产商的成本考虑,应选择方案二
17.答案:(1),;
(2)72.9;
(3)14
解析:(1)由题意知,
解得.
估计这200名员工所得分数的平均数
,
.
(2)的频率为,
的频率为,
所以中位数落在区间,设中位数为m,
所以,
解得,即估计这200名员工所得分数的中位数为72.9.
(3)的人数:,
的人数:,
的人数:,
所以这组中抽取的人数为:.
18.答案:(1)2人;
(2)71;
(3)
解析:(1)成绩在的人数为(人),
成绩在的人数为(人),
则按分层抽样方法从成绩低于60分的同学中抽取5人,
成绩低于50分的人数为(人).
故5人中成绩低于50分的人数为2人;
(2)由,得,
则平均数,
故该校学生首轮竞赛成绩的平均数约为71分;
(3)根据频率分布直方图可知:
的频率为,的频率为,
所以入围复赛的成绩一定在,
可知入围复赛的成绩的临界值为,
则,解得,
故估计入围复赛的成绩为分.
19.答案:(1),
(2)78分
(3)90;38.75
解析:(1)由题意知,所以,解得,
又,解得.
所以,,
(2)成绩落在内的频率为:,落在内的频率为:,设第80百分位数为m,
则,解得,所以晋级分数线划为78分合理.
(3),故:.又,,
剔除其中的95和85两个分数,设剩余8个数为,,,…,,平均数与标准差分别为,,则剩余8个分数的平均数:;
方差:.
【满分:150分】
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列各项调查中你认为合理的有( )
①为了了解全校同学喜欢课程情况,对某班男同学进行抽样调查
②“神舟十四号”飞船发射前,采用抽样调查的方式检查其各零部件的合格情况
③采用抽样调查的方式了解国内外观众对电影《流浪地球》的观影感受
④为调查我市居民对“垃圾分类”有关内容的了解程度,将要调查的问题放到某网站上,这样大部分上网的人就可以看到调查问题并及时反馈
A.0个 B.1个 C.2个 D.3个
2.随机抽查了某校100名高三学生的视力情况,得到的频率分布直方图如图所示,由于不慎将部分数据丢失,但知道后5组的频数和为64,设视力在4.6到4.8之间的学生人数为a,各组中频率最大的为0.34,则a的值为( )
A.64 B.54 C.48 D.27
3.“社保”已经走入了我们的生活,它包括养老保险、医疗保险、失业保险、工伤保险、生育保险,全年支出最重要的三项分别为养老保险、失业保险、工伤保险,下图是近五年三项社会保险基金的收支情况,下列说法中错误的是( )
A.三项社会保险基金在2020年以前收入为逐年递增
B.三项社会保险基金在2020年以前支出为逐年递增
C.三项社会保险基金在2016~2019年间收支并未出现“赤字”(收入低于支出)
D.2020年三项社会保险基金支出合计57580亿元,比上年增加3088亿元,约增长6.7%
4.下列抽样方法是简单随机抽样的是( )
A.质检员从50个零件中一次性抽取5个做质量检验
B.网课上,李老师对全班45名学生中点名表扬了3名发言积极的
C.老师要求学生从实数集中逐个抽取10个数分析奇偶性
D.某运动员从8条跑道中随机抽取1条跑道试跑
5.为了解学生体育锻炼情况,宜春中学随机抽取甲、乙两个班级,对这两个班级某一周内每天的人均体育锻炼时间(单位:min)进行了数据统计,得到如图所示的折线图,下列说法正确的是( )
A.班级乙该周每天的人均体育锻炼时间的极差比班级甲的小
B.班级甲该周每天的人均体育锻炼时间的中位数为72
C.班级乙该周每天的人均体育锻炼时间的众数为30
D.班级甲该周每天的人均体育锻炼时间的平均数比班级乙的大
6.已知某7个数的平均数为3,方差为3,现加入一个新数据3,此时这8个数的平均数为,标准差为s,则( )
A., B., C., D.,
7.某零件加工厂认定工人通过试用期的方法为:随机选取试用期中的5天,再从每天生产的零件中分别随机抽取25件,要求每天合格品均不低于22件.若甲、乙、丙三人在其5天抽检样本中的合格品件数统计如下,甲:中位数为24,极差不超过2;乙:平均数为23,方差不超过1;丙:众数为23,方差不超过1,则一定能通过试用期的有( )
A.甲、乙 B.甲、丙 C.乙、丙 D.甲、乙、丙
8.某校开展“正心立德,劳动树人”主题教育活动,对参赛的100名学生的劳动作品的得分情况进行统计,并绘制了如图所示的频率分布直方图(每组为左闭右开区间),根据图中信息,下列结论错误的是( )
A.图中的x值为0.020
B.得分在80分及以上的人数为40
C.这组数据平均数的估计值为77
D.这组数据第80百分位数的估计值为85
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列命题是真命题的有( )
A.分层抽样调查后的样本中甲、乙、丙三种个体的比例为,如果抽取的甲个体数为9,则样本容量为30
B.某一组样本数据为125,120,122,105,130,114,116,95,120,134,则样本数据落在区间内的频率为0.4
C.甲、乙两队队员体重的平均数分别为60,68,人数之比为,则甲、乙两队全部队员体重的平均数为67
D.一组数6,5,4,3,3,3,2,2,2,1的85%分位数为5
10.某校为了解学生对食堂的满意程度,设计了一份调查问卷,从该校高中生中随机抽取部分学生参加测试,记录了他们的分数,将收集到的学生测试分数按照,,,,,,分组,画出频率分布直方图,已知随机抽取的学生测试分数不低于80分的学生有27人,则以下结论中正确的是( )
A.此次测试众数的估计值为85
B.此次测试分数在的学生人数为6
C.随机抽取的学生测试分数的第55百分位数约为80
D.平均数m在中位数n右侧
11.某校开学初组织新生进行数学摸底测试,现从1000名考生中,随机抽取200人的成绩(满分为100分)作为样本,得到成绩的频率分布直方图如图所示,其中样本数据分组区间为,,,,,.则下列说法正确的是( )
A.
B.估计这次考试的分位数为82.4
C.在该样本中,若采用分层随机抽样的方法,从成绩低于60分和90分及以上的学生中共抽取10人,则应在中抽取2人
D.若成绩在60分及以上算合格,估计该校新生成绩合格的人数为860人
三、填空题:本题共3小题,每小题5分,共15分.
12.某学校为了解高一学生每天阅读时长,从高一男生和女生中采用分层抽样的方法抽取部分学生进行调查分析.已知该学校高一学生中男生和女生的比例是,在抽取的学生中男生比女生多24人,则被抽取的学生人数是________.
13.相关部门对某景区在“十一”黄金周中每天的游客人数做了统计,其频率分布如表所示:
时间 10月1日 10月2日 10月3日 10月4日 10月5日 10月6日 10月7日
频率 0.05 0.08 0.09 0.13 0.30 0.15 0.20
已知10月1日这天该景区的营业额约为8万元,假定这七天每天游客人均消费相同,则这个黄金周该景区游客人数最多的那一天的营业额约为_________万元.
14.一组数据按从小到大的顺序排列为1,4,4,x,7,8(其中),若该组数据的中位数是众数的倍,则该组数据的第60百分位数是__________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)为了了解甲、乙两个工厂生产的轮胎的宽度是否达标,分别从两厂随机选取了10个轮胎,将每个轮胎的宽度(单位:mm)记录下来并绘制出如下折线图.
(1)分别计算甲、乙两厂提供的10个轮胎宽度的平均数.
(2)若轮胎的宽度在内,则称这个轮胎是标准轮胎.
(ⅰ)若从甲厂提供的10个轮胎中随机选取1个,求所选的轮胎是标准轮胎的概率;
(ⅱ)试比较甲、乙两厂分别提供的10个轮胎中所有标准轮胎宽度的方差的大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个厂的轮胎相对更好.
16.(15分)已知某科技公司的某型号芯片的各项指标经过全面检测后,分为I级和Ⅱ级,两种品级芯片的某项指标的频率分布直方图如图所示:
若只利用该指标制定一个标准,需要确定临界值K,将该指标大于K的产品应用于A型手机,小于或等于K的产品应用于B型手机.假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.
(1)若临界值,请估计该公司生产的1000个该型号芯片I级品和1000个Ⅱ级品中应用于A型手机的芯片个数;
(2)设且,现有足够多的芯片I级品 Ⅱ级品,分别应用于A型手机 B型手机各1万部的生产:
方案一:直接将该芯片I级品应用于A型手机,其中该指标小于等于临界值K的芯片会导致芯片生产商每部手机损失800元;直接将该芯片Ⅱ级品应用于B型手机,其中该指标大于临界值K的芯片,会导致芯片生产商每部手机损失400元;
方案二:重新检测芯片I级品,Ⅱ级品的该项指标,并按规定正确应用于手机型号,会避免方案一的损失费用,但检测费用共需要130万元;
请求出按方案一,芯片生产商损失费用的估计值(单位:万元)的表达式,并从芯片生产商的成本考虑,选择合理的方案.
17.(15分)某公司为了解员工对食堂的满意程度,随机抽取了200名员工做了一次问卷调查,要求员工对食堂的满意程度进行打分,所得分数均在内,现将所得数据分成6组:,,,,,,并得到如图所示的频率分布直方图.
(1)求a的值,并估计这200名员工所得分数的平均数(同一组中的数据用该组区间的中点值代表);
(2)求这200名员工所得分数的中位数(精确到0.1);
(3)现从,,这三组中用比例分配的分层随机抽样的方法抽取24人,求这组中抽取的人数.
18.(17分)2023年秋末冬初,呼和浩特市发生了流感疾病.为了彻底击败病毒,人们更加讲究卫生讲究环保.某学校开展组织学生参加线上环保知识竞赛活动,现从中抽取200名学生,记录他们的首轮竞赛成绩并作出如图所示的频率直方图,根据图形,请回答下列问题:
(1)若从成绩低于60分的同学中按分层抽样方法抽取5人成绩,求5人中成绩低于50分的人数;
(2)以样本估计总体,利用组中值估计该校学生首轮竞赛成绩的平均数;
(3)首轮竞赛成绩位列前的学生入围第二轮的复赛,请根据图中信息,估计入围复赛的成绩(记为K).
19.(17分)2024年5月22日至5月28日是第二届全国城市生活垃圾分类宣传周,本次宣传周的主题为“践行新时尚分类志愿行”.阜阳三中高一年级举行了一次“垃圾分类知识竞赛”,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩x(单位:分,得分取正整数,满分为100分)作为样本进行统计将成绩进行整理后,分为五组(,,,,),其中第1组频数的平方等于第2组、第4组频数之积,请根据下面尚未完成的频率分布直方图(如图所示)解决下列问题:
(1)求a,b的值;
(2)若根据这次成绩,学校准备淘汰的同学,仅留的同学进入下一轮竞赛请问晋级分数线划为多少合理
(3)某老师在此次竞赛成绩中抽取了10名学生的分数:,,,…,,已知这10个分数的平均数,标准差,若剔除其中的95和85这两个分数,求剩余8个分数的平均数与方差.
答案以及解析
1.答案:B
解析:①了解全校同学喜欢课程情况,应在各班进行抽样,同时不能仅限男同学,不合理;
②“神舟十四号”飞船发射前,应采用全面调查检查其各零部件的合格情况,不合理;
③了解国内外观众对电影《流浪地球》的观影感受,采用抽样调查,合理;
④对“垃圾分类”有关内容的了解程度,问题放到某网站上,受调查人群有局限,不合理.
故选:B.
2.答案:B
解析:由题意知,前两组的频数之和为,第四组的频数为,后五组的频数之和为64,所以前二组的频数之和为,故第三组的频数为,因此.故选B.
3.答案:D
解析:由条形图可知,三项社会保险基金在2020年以前收入为逐年递增的,故A正确;
三项社会保险基金在2020年以前支出为逐年递增的,故B正确;
三项社会保险基金在2016~2019年间收支并未出现“赤字”,故C正确;
2020年三项社会保险基金支出合计57580亿元,比上年增加3088亿元,约增长,故D错误.故选D.
4.答案:D
解析:选项A,一次性抽取不是逐个不放回地抽取,不符合简单随机抽样的要求,故A错误;
选项B,老师表扬的是发言积极的,对每一个个体而言,不具备“等可能性:”,故B错误;
选项C,因为总体容量是无限的,不符合简单随机抽样的要求,故C错误;
选项D,8条跑道,抽取1条,总体有限,每个个体被抽到的机会均等,是简单随机抽样,故D正确.故选D.
5.答案:C
解析:由题意可知,班级甲的数据按从小到大的顺序排列得30,35,55,65,70,70,72;
班级乙的数据按从小到大的顺序排列得30,30,35,65,83,88,90.
对于选项A:班级甲的极差为,班级乙的极差为,
所以班级乙该周每天的人均体育锻炼时间的极差比班级甲的大,故A错误;
对于选项B:班级甲该周每天的人均体育锻炼时间的中位数为65,故B错误;
对于选项C:班级乙该周每天的人均体育锻炼时间的众数为30,故C正确;
对于选项D:班级甲的平均数,班级乙的平均数,所以班级甲该周每天的人均体育锻炼时间的平均数比班级乙的小,故D错误.故选C.
6.答案:B
解析:某7个数的平均数为3,方差为3,现加入一个新数据3,此时这8个数的平均数为,标准差为s,方差为,,,.故选B.
7.答案:A
解析:对于甲:由甲的统计数据可知,甲至少有3天的合格品数不低于24,最低合格品数不低于2,所以甲一定能通过;
对于乙:设乙每天的合格品件数为,,则,
即.若乙有不止一天的合格品数低于21,,不合题意;
若乙只有一天的合格品数低于22,不妨取,,因为平均数为23,则至少有一天的合格品数为25或至少有两天的合格品数为24,无论哪种情况,都可以得到,不合题意,所以乙的每一天的合格品数都不低于22,乙一定能通过;
对于丙:若丙的合格品数为21,22,23,23,23,则丙的众数为23,方差为0.64,符合丙的统计数据,但丙不能通过;
所以甲、乙一定能通过,A正确;
故选:A.
8.答案:D
解析:由频率之和为1得,解得,A正确,不符合题意;得分在80分及以上的人数为,B正确,不符合题意;因为,所以C正确,不符合题意;因为,,所以这组数据第80百分位数的估计值落在区间内,,故这组数据第80百分位数的估计值不为85,D错误,符合题意.故选D.
9.答案:BD
解析:对于选项A:根据样本的抽样比等于各层的抽样比,得样本容量为,故选项A为假命题;
对于选项B:样本数据落在区间内的有120,122,116,120,共4个,所以样本数据落在区间内的频率为,故选项B为真命题;
对于选项C:甲、乙两队的人数之比为,则甲队队员在所有队员中所占比例为,乙队队员在所有队员中所占比例为,则甲、乙两队全部队员体重的平均数为,故选项C为假命题;
对于选项D:将该组数据从小到大排列为1,2,2,2,3,3,3,4,5,6,由,则该组数据的分位数是第9个数,该数为5,故选项D为真命题.
10.答案:ABC
解析:由直方图可知此次测试众数的估计值为85,故A正确;因为不低于80分的学生的频率为,所以该校高中生中随机抽取的学生人数为,所以此次测试分数在的学生人数为,故B正确;因为,所以随机抽取的学生测试分数的第55百分位数约为80,故C正确;由直方图在左边“拖尾”可知平均数小于中位数,即平均数m在中位数n左侧,故D错误.故选ABC.
11.答案:BD
解析:对于A:由得,故A错误;
对于B:成绩在区间所占的频率为,成绩在区间所占的频率为,故分位数所在区间为,设分位数为x,则,解得,故B正确;
对于C:低于60分和90分及以上的学生占的频率之和为,成绩在占的频率为,故按分层抽样,应在中抽取的人数为人,故C错误;
对于D:估计该校新生成绩在60以下的人数为,故估计该校新生成绩合格的人数为人,故D正确.故选BD.
12.答案:168
解析:设抽取的学生中男生人数为a,女生人数为b,则,且,解得,,则被抽取的学生人数是.故答案为168.
13.答案:48
解析:设游客人数最多的那一天的营业额约为x万元.由,解得.故游客人数最多的那一天的营业额约为48万元.
14.答案:6
解析:由题意知,众数是4,则中位数为,则,解得,又,则第60百分位数是6.
故答案为:6.
15.答案:(1);
(2)(ⅰ)
(ⅱ)乙厂的轮胎相对更好
解析:(1)甲厂提供的10个轮胎宽度的平均数
.
乙厂提供的10个轮胎宽度的平均数
.
(2)甲厂提供的这10个轮胎的宽度在内的数据为195,194,196,194,196,195.
(ⅰ)所选的轮胎是标准轮胎的概率.
(ⅱ)计算得甲厂提供的10个轮胎中标准轮胎宽度的平均数为195,方差为.
乙厂提供的这10个轮胎的宽度在内的数据为195,196,195,194,195,195,计算得平均数为195,方差为.
由样本估计总体,两厂标准轮胎宽度的平均数相等,但乙的方差较小,所以乙厂的轮胎相对更好.
16.答案:(1)1030;
(2),应选择方案二
解析:(1)临界值时,I级品中该指标大于60的频率为,
Ⅱ级品中该指标大于60的频率为0.1
故该公司生产的1000个该型号芯片I级品和1000个Ⅱ级品中应用于A型手机的芯片个数估计为:
(2)当临界值时,若采用方案一:
I级品中该指标小于或等于临界值K的概率为,可以估计10000部A型手机中有部手机芯片应用错误;
Ⅱ级品中该指标大于临界值K的概率为,
可以估计10000部B型手机中有部手机芯片应用错误;
故可以估计芯片生产商的损失费用
,
又采用方案二需要检测费用共130万元
故从芯片生产商的成本考虑,应选择方案二
17.答案:(1),;
(2)72.9;
(3)14
解析:(1)由题意知,
解得.
估计这200名员工所得分数的平均数
,
.
(2)的频率为,
的频率为,
所以中位数落在区间,设中位数为m,
所以,
解得,即估计这200名员工所得分数的中位数为72.9.
(3)的人数:,
的人数:,
的人数:,
所以这组中抽取的人数为:.
18.答案:(1)2人;
(2)71;
(3)
解析:(1)成绩在的人数为(人),
成绩在的人数为(人),
则按分层抽样方法从成绩低于60分的同学中抽取5人,
成绩低于50分的人数为(人).
故5人中成绩低于50分的人数为2人;
(2)由,得,
则平均数,
故该校学生首轮竞赛成绩的平均数约为71分;
(3)根据频率分布直方图可知:
的频率为,的频率为,
所以入围复赛的成绩一定在,
可知入围复赛的成绩的临界值为,
则,解得,
故估计入围复赛的成绩为分.
19.答案:(1),
(2)78分
(3)90;38.75
解析:(1)由题意知,所以,解得,
又,解得.
所以,,
(2)成绩落在内的频率为:,落在内的频率为:,设第80百分位数为m,
则,解得,所以晋级分数线划为78分合理.
(3),故:.又,,
剔除其中的95和85两个分数,设剩余8个数为,,,…,,平均数与标准差分别为,,则剩余8个分数的平均数:;
方差:.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
