江苏省南京市金陵中学河西分校2024-2025学年九年级上学期期初考试数学试题(PDF版,无答案)
文档属性
| 名称 | 江苏省南京市金陵中学河西分校2024-2025学年九年级上学期期初考试数学试题(PDF版,无答案) |  | |
| 格式 | |||
| 文件大小 | 425.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-06 21:51:04 | ||
图片预览

文档简介
初三年级数学限量限时练习试卷
一、选择题(每题 2 分,共 12 分)
1. 若关于 x的方程 ax2+3x+1=0是一元二次方程,则 a满足的条件是 ( )
A.a 9≤ B.a>0 C.a≠0 D 4.a>
4 9
2.一元二次方程 x2-6x+5=0配方可变形为 ( )
A.(x-3)2=4 B.(x+3)2=14 C.(x-3)2=14. D.(x+3)2=4
3.下列说法:①同一圆上的点到圆心的距离相等;②如果某几个点到一个定点的距离相等,则这几个点
共圆;③半径确定了,圆就确定了,其中正确的是 ( )
A.①② B.①③ C.②③ D.①②③
4.下列方程中,两个实数根的和等于 2的方程是 ( )
A.2x2-4x+3=0 B.2x2-2x-3=0 C.2y2+4y-3=0 D.2t2-4t-3=0
5.如图,四边形 ABCD的对角线 AC、BD相交于点 O,且将这个四边形分成①②③④四个三角形,
若 OA∶OC=OB∶OD,则下列结论正确的是 ( )
A.①和②相似 B.①和③相似 C.①和④相似 D.②和④相似
6.如图,已知在等腰 Rt△ABC中,∠ACB=90°,AD为 BC边的中线,过点 C作 CE⊥AD于点 E,交
AB于点 F.若 AC=2,则线段 EF的长为 ( )
A 3. B 4 5 C 2 5. . D 2.
5 15 15 3
O.
A B
(第 5题) (第 6题) (第 9题)
二、填空题(每题 2 分,共 20 分)
7.若一元二次方程 x2-2x+c=0有两个相等的实数根,则 c的值为 .
8.两个相似多边形的相似比为 1:2,则它们周长的比为 .
9.如图,在⊙O中,若∠AOB=120°,则弦 AB所对的弧的度数为 .
10.如图,D、E分别在△ABC边 AB、AC上,若 DE∥BC,AD=2DB,DE=4,则 BC的长为 .
11.物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图象投影的方法.如图,燃烧
的蜡烛(竖直放置)AB经小孔 O在屏幕(竖直放置)上成像 A′B′,设 AB=36cm,A′B′=24cm,小
孔 O到 AB的距离为 30cm,则小孔 O到 A′B′的距离为 cm.
A
D E P
B C Q
(第 10题) (第 11题) (第 12题)
{#{QQABKYCAwU5oggCQAkAJJaIAACRJ5gLCAA0wEVMYCCEEmCQkkIBCAhALUAgQsgQORxANAuAAoZAKIAQgYRNAABBIAA=}=#}}#}
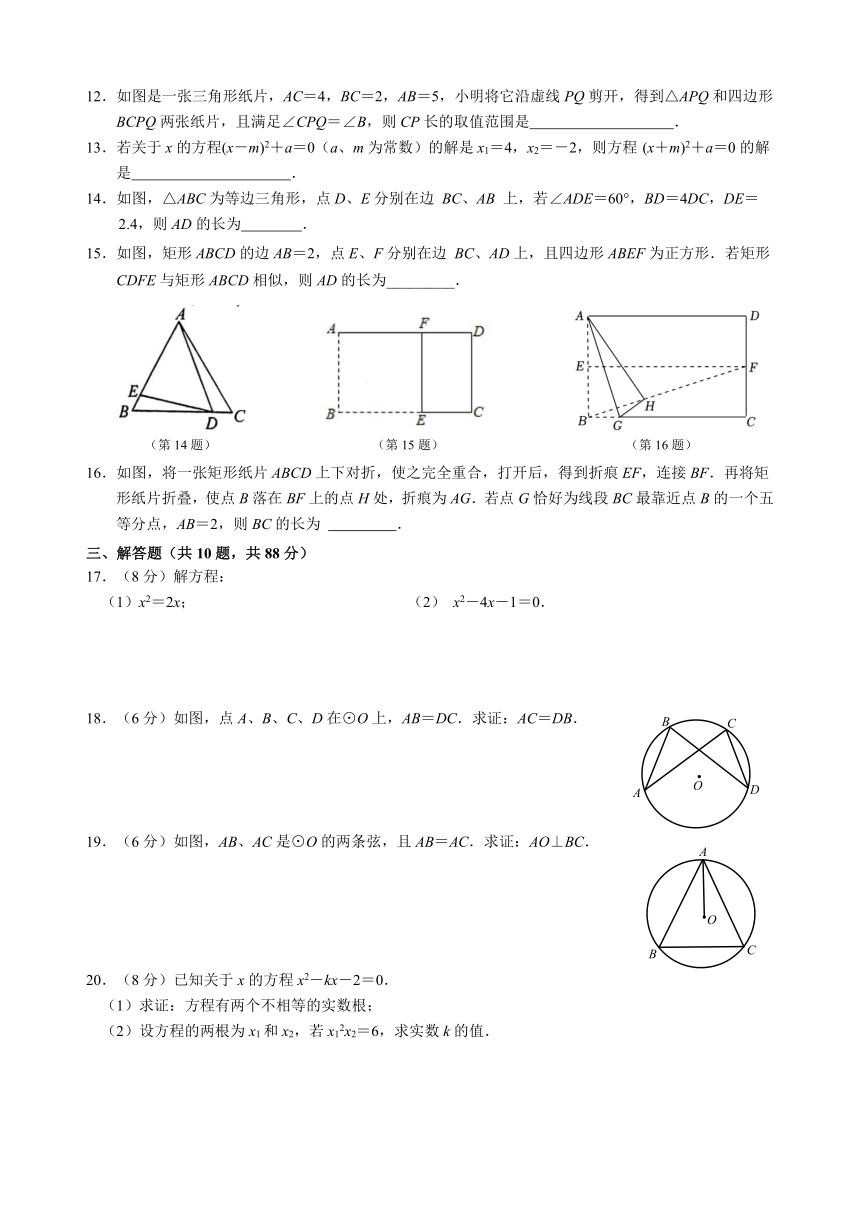
12.如图是一张三角形纸片,AC=4,BC=2,AB=5,小明将它沿虚线 PQ剪开,得到△APQ和四边形
BCPQ两张纸片,且满足∠CPQ=∠B,则 CP长的取值范围是 .
13.若关于 x的方程(x-m)2+a=0(a、m为常数)的解是 x1=4,x2=-2,则方程 (x+m)2+a=0的解
是 .
14.如图,△ABC为等边三角形,点 D、E分别在边 BC、AB 上,若∠ADE=60°,BD=4DC,DE=
2.4,则 AD的长为 .
15.如图,矩形 ABCD的边 AB=2,点 E、F分别在边 BC、AD上,且四边形 ABEF为正方形.若矩形
CDFE与矩形 ABCD相似,则 AD的长为_________.
(第 14题) (第 15题) (第 16题)
16.如图,将一张矩形纸片 ABCD上下对折,使之完全重合,打开后,得到折痕 EF,连接 BF.再将矩
形纸片折叠,使点 B落在 BF上的点 H处,折痕为 AG.若点 G恰好为线段 BC最靠近点 B的一个五
等分点,AB=2,则 BC的长为 .
三、解答题(共 10 题,共 88 分)
17.(8分)解方程:
(1)x2=2x; (2) x2-4x-1=0.
18.(6分)如图,点 A、B、C、D在⊙O上,AB=DC.求证:AC=DB. B C
A O
· D
19.(6分)如图,AB、AC是⊙O的两条弦,且 AB=AC.求证:AO⊥BC.
A
·O
B C
20.(8分)已知关于 x的方程 x2-kx-2=0.
(1)求证:方程有两个不相等的实数根;
(2)设方程的两根为 x1和 x2,若 x12x2=6,求实数 k的值.
{#{QQABKYACwU5oggCQAkAJJaIAACRJ5gLCAA0wEVMYCCEEmCQkkIBCAhALUAgQsgQORxANAuAAoZAKIAQgYRNAABBIAA=}=#}}#}
21.(8分)如图,AB是⊙O的直径,点 C,D在⊙O上,若⌒AD=⌒CD.
求证:OD∥BC.
22.(8分)如图,网格中的每个小正方形的边长都是 1,每个小正方形的顶点叫做格点,以格点为顶点,
分别按下列要求画三角形.
(1)在图②中,请在网格中画一个与图①△ABC相似的△DEF;
(2)在图③中,以 O为位似中心,画一个△A1B1C1,使它与△ABC的位似比为 2∶1.
23.(10分)如图,在矩形 ABCD中,E是 AD边的中点,BE⊥AC,垂足为点 F.
(1)求证:FC=2FA;
(2)若 EF=1,则 AC的长为 ;
(3)连接 DF,求证:DC=DF.
24.(10分)一块直角三角形木板,它的一条直角边 AC长为 2m,面积为 1.5 m2.现在要把它加工成一
个面积最大的正方形桌面.甲、乙两位同学的加工方法分别如图①、图②所示.请用学过的知识说
明哪位同学的加工方法符合要求.
{#{QQABKYCAwU5oggCQAkAJJaIAACRJ5gLCAA0wEVMYCCEEmCQkkIBCAhALUAgQsgQORxANAuAAoZAKIAQgYRNAABBIAA=}=#}}#}
25.(12分)
[模型建立]
如图①、②,点 P分别在⊙O外、在⊙O内,直线 PO分别交⊙O于点 A、B,则 PA是点 P到⊙O
上的点的最短距离,PB是点 P到⊙O上的点的最长距离.
P O O PB A
A B
图① 图②
[问题解决]
请就图①中 PB为何最长进行证明.
[初步应用]
(1)已知点 P到⊙O上的点的最短距离为 3,最长距离为 7.则⊙O的半径为 .
(2)如图③,在△ABC中,∠C=90°,AC=8,BC=6.点 E在边 BC上,且 CE=2,动点 P在半径
为 2的⊙E上,则 AP的最小值是 .
B y
B ·P
P
. CE
C A O A x
图③ 图④
[拓展延伸]
如图④,点 A(2,0),动点 B在以 P (4,4)为圆心, 2为半径的圆上,OB的中点为 C,则线段 AC
的最大值为 .
26.(12分)如图 1,在△ABC中,∠C=90°,∠A=30°,BC=1,点 D,E分别为 AC,BC的中点.
△CDE绕点 C顺时针旋转,设旋转角为α(0°≤α≤360°),记直线 AD与直线 BE的交点为点 P.
(1)如图 1,当α=0°时,AD与 BE的数量关系为 ,位置关系为 ;
(2)当 0°<α≤360°时,上述结论是否成立?若成立,请仅就图 2的情形进行证明;若不成立,请说明
理由;
(3)△CDE绕点 C顺时针旋转一周,请直接写出运动过程中 P点运动轨迹的长度和 P点到直线 BC距
离的最大值.
{#{QQABKYCAwU5oggCQAkAJJaIAACRJ5gLCAA0wEVMYCCEEmCQkkIBCAhALUAgQsgQORxANAuAAoZAKIAQgYRNAABBIAA=}=#}}#}
一、选择题(每题 2 分,共 12 分)
1. 若关于 x的方程 ax2+3x+1=0是一元二次方程,则 a满足的条件是 ( )
A.a 9≤ B.a>0 C.a≠0 D 4.a>
4 9
2.一元二次方程 x2-6x+5=0配方可变形为 ( )
A.(x-3)2=4 B.(x+3)2=14 C.(x-3)2=14. D.(x+3)2=4
3.下列说法:①同一圆上的点到圆心的距离相等;②如果某几个点到一个定点的距离相等,则这几个点
共圆;③半径确定了,圆就确定了,其中正确的是 ( )
A.①② B.①③ C.②③ D.①②③
4.下列方程中,两个实数根的和等于 2的方程是 ( )
A.2x2-4x+3=0 B.2x2-2x-3=0 C.2y2+4y-3=0 D.2t2-4t-3=0
5.如图,四边形 ABCD的对角线 AC、BD相交于点 O,且将这个四边形分成①②③④四个三角形,
若 OA∶OC=OB∶OD,则下列结论正确的是 ( )
A.①和②相似 B.①和③相似 C.①和④相似 D.②和④相似
6.如图,已知在等腰 Rt△ABC中,∠ACB=90°,AD为 BC边的中线,过点 C作 CE⊥AD于点 E,交
AB于点 F.若 AC=2,则线段 EF的长为 ( )
A 3. B 4 5 C 2 5. . D 2.
5 15 15 3
O.
A B
(第 5题) (第 6题) (第 9题)
二、填空题(每题 2 分,共 20 分)
7.若一元二次方程 x2-2x+c=0有两个相等的实数根,则 c的值为 .
8.两个相似多边形的相似比为 1:2,则它们周长的比为 .
9.如图,在⊙O中,若∠AOB=120°,则弦 AB所对的弧的度数为 .
10.如图,D、E分别在△ABC边 AB、AC上,若 DE∥BC,AD=2DB,DE=4,则 BC的长为 .
11.物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图象投影的方法.如图,燃烧
的蜡烛(竖直放置)AB经小孔 O在屏幕(竖直放置)上成像 A′B′,设 AB=36cm,A′B′=24cm,小
孔 O到 AB的距离为 30cm,则小孔 O到 A′B′的距离为 cm.
A
D E P
B C Q
(第 10题) (第 11题) (第 12题)
{#{QQABKYCAwU5oggCQAkAJJaIAACRJ5gLCAA0wEVMYCCEEmCQkkIBCAhALUAgQsgQORxANAuAAoZAKIAQgYRNAABBIAA=}=#}}#}
12.如图是一张三角形纸片,AC=4,BC=2,AB=5,小明将它沿虚线 PQ剪开,得到△APQ和四边形
BCPQ两张纸片,且满足∠CPQ=∠B,则 CP长的取值范围是 .
13.若关于 x的方程(x-m)2+a=0(a、m为常数)的解是 x1=4,x2=-2,则方程 (x+m)2+a=0的解
是 .
14.如图,△ABC为等边三角形,点 D、E分别在边 BC、AB 上,若∠ADE=60°,BD=4DC,DE=
2.4,则 AD的长为 .
15.如图,矩形 ABCD的边 AB=2,点 E、F分别在边 BC、AD上,且四边形 ABEF为正方形.若矩形
CDFE与矩形 ABCD相似,则 AD的长为_________.
(第 14题) (第 15题) (第 16题)
16.如图,将一张矩形纸片 ABCD上下对折,使之完全重合,打开后,得到折痕 EF,连接 BF.再将矩
形纸片折叠,使点 B落在 BF上的点 H处,折痕为 AG.若点 G恰好为线段 BC最靠近点 B的一个五
等分点,AB=2,则 BC的长为 .
三、解答题(共 10 题,共 88 分)
17.(8分)解方程:
(1)x2=2x; (2) x2-4x-1=0.
18.(6分)如图,点 A、B、C、D在⊙O上,AB=DC.求证:AC=DB. B C
A O
· D
19.(6分)如图,AB、AC是⊙O的两条弦,且 AB=AC.求证:AO⊥BC.
A
·O
B C
20.(8分)已知关于 x的方程 x2-kx-2=0.
(1)求证:方程有两个不相等的实数根;
(2)设方程的两根为 x1和 x2,若 x12x2=6,求实数 k的值.
{#{QQABKYACwU5oggCQAkAJJaIAACRJ5gLCAA0wEVMYCCEEmCQkkIBCAhALUAgQsgQORxANAuAAoZAKIAQgYRNAABBIAA=}=#}}#}
21.(8分)如图,AB是⊙O的直径,点 C,D在⊙O上,若⌒AD=⌒CD.
求证:OD∥BC.
22.(8分)如图,网格中的每个小正方形的边长都是 1,每个小正方形的顶点叫做格点,以格点为顶点,
分别按下列要求画三角形.
(1)在图②中,请在网格中画一个与图①△ABC相似的△DEF;
(2)在图③中,以 O为位似中心,画一个△A1B1C1,使它与△ABC的位似比为 2∶1.
23.(10分)如图,在矩形 ABCD中,E是 AD边的中点,BE⊥AC,垂足为点 F.
(1)求证:FC=2FA;
(2)若 EF=1,则 AC的长为 ;
(3)连接 DF,求证:DC=DF.
24.(10分)一块直角三角形木板,它的一条直角边 AC长为 2m,面积为 1.5 m2.现在要把它加工成一
个面积最大的正方形桌面.甲、乙两位同学的加工方法分别如图①、图②所示.请用学过的知识说
明哪位同学的加工方法符合要求.
{#{QQABKYCAwU5oggCQAkAJJaIAACRJ5gLCAA0wEVMYCCEEmCQkkIBCAhALUAgQsgQORxANAuAAoZAKIAQgYRNAABBIAA=}=#}}#}
25.(12分)
[模型建立]
如图①、②,点 P分别在⊙O外、在⊙O内,直线 PO分别交⊙O于点 A、B,则 PA是点 P到⊙O
上的点的最短距离,PB是点 P到⊙O上的点的最长距离.
P O O PB A
A B
图① 图②
[问题解决]
请就图①中 PB为何最长进行证明.
[初步应用]
(1)已知点 P到⊙O上的点的最短距离为 3,最长距离为 7.则⊙O的半径为 .
(2)如图③,在△ABC中,∠C=90°,AC=8,BC=6.点 E在边 BC上,且 CE=2,动点 P在半径
为 2的⊙E上,则 AP的最小值是 .
B y
B ·P
P
. CE
C A O A x
图③ 图④
[拓展延伸]
如图④,点 A(2,0),动点 B在以 P (4,4)为圆心, 2为半径的圆上,OB的中点为 C,则线段 AC
的最大值为 .
26.(12分)如图 1,在△ABC中,∠C=90°,∠A=30°,BC=1,点 D,E分别为 AC,BC的中点.
△CDE绕点 C顺时针旋转,设旋转角为α(0°≤α≤360°),记直线 AD与直线 BE的交点为点 P.
(1)如图 1,当α=0°时,AD与 BE的数量关系为 ,位置关系为 ;
(2)当 0°<α≤360°时,上述结论是否成立?若成立,请仅就图 2的情形进行证明;若不成立,请说明
理由;
(3)△CDE绕点 C顺时针旋转一周,请直接写出运动过程中 P点运动轨迹的长度和 P点到直线 BC距
离的最大值.
{#{QQABKYCAwU5oggCQAkAJJaIAACRJ5gLCAA0wEVMYCCEEmCQkkIBCAhALUAgQsgQORxANAuAAoZAKIAQgYRNAABBIAA=}=#}}#}
同课章节目录
