第十二周—八年级上册数学北师大版(2012)每周测验考查范围:6.2-6.4(含解析)
文档属性
| 名称 | 第十二周—八年级上册数学北师大版(2012)每周测验考查范围:6.2-6.4(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 878.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-06 21:15:01 | ||
图片预览




文档简介
第十二周—八年级上册数学北师大版(2012)每周测验
考查范围:6.2-6.4
1.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示.
成绩/米 1.50 1.60 1.65 1.70 1.75
人数 2 3 5 4 1
这些运动员成绩的众数和中位数分别为( )
A.1.65米,1.65米 B.1.65米,1.70米 C.1.75米,1.65米 D.1.50米,1.60米
2.七名同学某月阅读课外书的数量分别是6,3,3,4,5,4,3(单位:本),小明该月阅读了x本课外书,将x添加到前面这组数据后,这列数的中位数不变,则x可能是( )
A.1 B.2 C.3 D.4
3.同学A在计算方差时使用了一个不完整的计算公式,,同学B则根据这个公式计算出了下列结果,同学A却说,同学B有一个结论错了,你认为错误的是( )
A. B. C.众数为3 D.中位数为3
4.如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 185 180 185 180
方差 3.6 3.6 7.4 8.1
根据表数据,从中选择一名成绩好且发挥稳定的参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
5.乡村医生李医生在对本村老年人进行年度免费体检时,发现张奶奶血压偏高,为了准确诊断,随后7天,李医生每天定时为张奶奶测量血压,测得数据如下表:
测量时间 第1天 第2天 第3天 第4天 第5天 第6天 第7天
收缩压(毫米汞柱) 151 148 140 139 140 136 140
舒张压(毫米汞柱) 90 92 88 88 90 80 88
对收缩压,舒张压两组数据分别进行统计分析,其中错误的是( )
A.收缩压的中位数为139 B.舒张压的众数为88
C.收缩压的平均数为142 D.舒张压的方差为
6.某企业生产厚度为的精密零件,为严把质量关,分别从A、B两车间随机抽出了50个精密零件,测量厚度,并将数据处理后制成如下表格,根据表中信息判断,下列说法错误的是( )
个数 平均厚度 厚度的方差
A车间 50
B车间 50
A.A、B两车间被抽出精密零件的平均厚度相同
B.本次采用的调查方式是抽样调查
C.被抽取的100个零件的厚度是本次调查的样本
D.B车间精密零件的厚度比A车间精密零件的厚度波动大
7.为了减轻学生课外作业负担,数学老师准备按照学生每天课外作业完成量(完成题目数量)实行分档布置作业.作业量分档递增,计划使第一档、第二档和第三档的作业量分别覆盖全校学生,和,为合理确定各档之间的界限,随机抽查了该校500名学生过去一段时间每天课外作业完成量的平均数(单位:个),并绘制了如下统计图(每组不包含最小值,包含最大值).下面四个推断合理的是( )
A.每天课外作业完成量不超过15个题的该校学生按第二档布置作业
B.每天课外作业完成量超过21个的该校学生按第三档布置作业
C.该校学生每天课外作业完成量的平均数不超过18个
D.该校学生每天课外作业完成量的中位数在15~18个之间
8.已知一组数据,,的方差是,则新的一组数据,,的方差是( )
A. B. C. D.
9.甲、乙、丙三位选手各10次射击,成绩的平均数均为93环,方差(单位:环)依次分别为0.026、0.015、0.032,则射击成绩最稳定的选手是____________(填“甲”、“乙”、“丙”中的一个).
10.跳远运动员小李在一次训练中,先跳了6次的成绩如下:,,,,,(单位:m),这六次成绩的平均数为,方差为.如果小李再跳一次,成绩为(单位:m),则小李这7次跳远成绩与前6次的成绩相比较,其方差___________(填“变大”或“变小”或“不变”)
11.学校抽查了30名学生参加学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的次数的中位数是___________.
12.数学老师布置了10道选择题作为课堂练习,课代表将全班同学的答题情况绘制成了如图的统计图,根据统计图,全班每位同学答对的题数所组成的一组数据的中位数为m道,众数为n道,则_______.
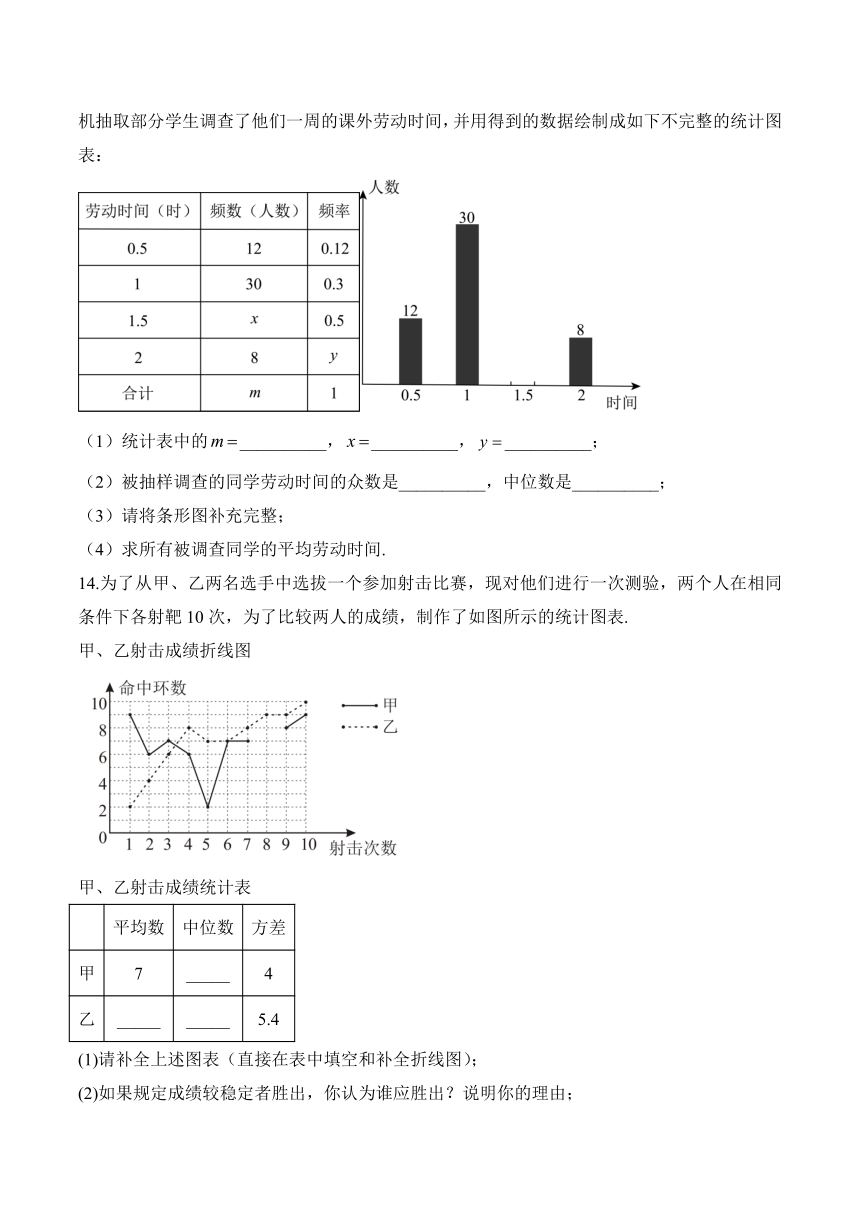
13.2022年3月25日,教育部印发《务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校为了解该校学生一周的课外劳动情况,随机抽取部分学生调查了他们一周的课外劳动时间,并用得到的数据绘制成如下不完整的统计图表:
(1)统计表中的__________,__________,__________;
(2)被抽样调查的同学劳动时间的众数是__________,中位数是__________;
(3)请将条形图补充完整;
(4)求所有被调查同学的平均劳动时间.
14.为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如图所示的统计图表.
甲、乙射击成绩折线图
甲、乙射击成绩统计表
平均数 中位数 方差
甲 7 _____ 4
乙 _____ _____ 5.4
(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果甲选手又射靶一次,射中了7环,和之前的10次成绩的数据结合后,甲选手射击成绩的平均数______;中位数______;方差______.(填“变大”“变小”或“不变”)
答案以及解析
1.答案:A
解析:观察表中可知,1.65出现了5次,次数最多,
运动员的成绩的众数为:1.65米.
将表中的数据按照从小到大的顺序排列如下:
1.50,1.50,1.60,1.60,1.60,1.65,1.65,1.65,1.65,1.65,1.70,1.70,1.70,1.70,1.75
运动员的成绩的中位数是1.65米.
故选:A.
2.答案:D
解析:将这组数据从小到大排列为:3,3,3,4,4,5,6,则中位数为4,
增加一个数x后,这列数的中位数仍不变,
则这组数据从小到大排列为:3,3,3,4,x,4,5,6,或3,3,3,x,4,4,5,6,
,
解得.
故选:D.
3.答案:A
解析:
平均数是3,
,
,故B不符合题意;
,故A符合题意;
从小到大排列为:1,2,3,3,6,
样本众数是3,故选项C不合题意;
中位数为3,故选项D不符合题意;
故选:A.
4.答案:A
解析:∵=>=,
∴从甲和丙中选择一人参加比赛,
∵,
∴选择甲参赛,
故选A.
5.答案:A
解析:把收缩压的数据按照从小到大的顺序排列为:
136,139,140,140,140,148,151;
排在最中间的数据是140,可得中位数为140,故A符合题意;
收缩压的平均数为:,故C不符合题意;
舒张压的数据中88出现3次,所以舒张压的数据的众数为88,故D不符合题意;
舒张压的平均数为:,
舒张压的方差为:;故D不符合题意;
故选A.
6.答案:D
解析:A、A、B两车间被抽出精密零件的平均厚度相同是正确的,不符合题意∶
B、两个车间的零件数量较多,不能采用普查,要用抽样调查是正确的,不符合题意;
C、被抽取的100个零件的厚度是本次调查的样本是正确的,不符合题意;
D、,A车间精密零件的厚度比A车间精密零件的厚度波动大,原说法错误,符合题意.
故选:D.
7.答案:C
解析:A选项,由统计图可得该校500名学生过去一段时间每天课外作业完成量的平均数不超过15个题的有(名),,故每天课外作业完成量不超过15个题的该校学生按第一档布置作业,故该选项错误,不符合题意;B选项,因为该校500名学生过去一段时间每天课外作业完成量的平均数超过21个题的有(名),,故此选项错误,不符合题意;C选项,通过计算加权平均数得,该校学生每天课外作业完成量的平均数不超过18个,正确,符合题意;D选项,因为按从小到大的顺序排列的500个数据的中位数是第250和251个数据的平均数,由统计图可知,第250和251个数据分别在9~12和12~15之间,所以其中位数应该在9~15之间,故此选项错误,不符合题意.故选C.
8.答案:A
解析:设这组数据,,的平均数为,方差,则另一组新数据,,的平均数为,方差为,
,
=
=
故选:A.
9.答案:乙
解析:甲、乙、丙三位选手各10次射击,
方差依次分别为:0.026、0.015、0.032,.
则射击成绩最稳定的选手是乙.
10.答案:变小
解析:小李再跳一次,成绩为,
这组数据的平均数是(m),
这7次跳远成绩的方差是:
,
,
方差变小,
故答案为:变小.
11.答案:3
解析:这组数据共有个,按顺序排列后位于中间的是第15和16个数,这两个数都是3,
中位数为:.
即30名学生参加活动的次数的中位数是3,
故答案为:3.
12.答案:17
解析:由统计图可知,在这组数据中7出现了4次,8出现了20次,9出现了18次,10出现了8次,所以8是出现次数最多的数据,所以这组数据的众数是8道.因为这组数据共有(个),所以中位数是第25个数据和第26个数据的平均数.因为这两个数据都是9,所以这组数据的中位数是9道,所以.
13.答案:(1)100,50,0.08
(2)1.5,1.5
(3)见解析
(4)所有被调查同学的平均劳动时间是1.27小时
解析:(1),,.
故答案为:100,50,0.08;
(2)被抽样调查的同学劳动时间数据中,
出现的次数最多的是1.5,故这组数据的众数为1.5;
参与调查的学生人数一共有100人,将他们的劳动时间从低到高排列,处在第50名和第51名的劳动时间分别为1.5和1.5,
中位数为.
故答案为:1.5,1.5;
(3)补画条形统计图如下:
(4)(小时).
答:所有被调查同学的平均劳动时间是1.27小时.
14.答案:(1)见解析
(2)甲应胜出;理由:甲、乙二人射击成绩的平均数相同,而甲射击成绩的方差小于乙,说明甲发挥得更稳定,所以甲应胜出
(3)不变;不变;变小
解析:(1)根据折线统计图得:
甲的射击成绩为9,6,7,6,2,7,7,?,8,9,平均数为7环,
则甲第八环成绩为(环),
所以甲的10次成绩为:9,6,7,6,2,7,7,9,8,9,
把这些数从小到大排列为2,6,6,7,7,7,8,9,9,9,
则中位数是:(环),
乙的射击成绩为:2,4,6,8,7,7,8,9,9,10,
则平均数为:(环),
把这些数从小到大排列为2,4,6,7,7,8,8,9,9,10,
则中位数是:(环),
补统计表如下:
平均数 中位数 方差
甲 7 7 4
乙 7 7.5 5.4
补全折线统计图如下:
(2)甲应胜出;
理由:甲、乙二人射击成绩的平均数相同,而甲射击成绩的方差小于乙,说明甲发挥得更稳定,所以甲应胜出;
(3)由(1)知平均数为7,增加1次射中7环后,则平均数不变;
中位数是第6个数,仍然是7环不变;
方差变小,理由是乙的新方差的分子的值不变,但是分母的值变大了,故新方差的值变小了;
故答案为:不变;不变;变小.
考查范围:6.2-6.4
1.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示.
成绩/米 1.50 1.60 1.65 1.70 1.75
人数 2 3 5 4 1
这些运动员成绩的众数和中位数分别为( )
A.1.65米,1.65米 B.1.65米,1.70米 C.1.75米,1.65米 D.1.50米,1.60米
2.七名同学某月阅读课外书的数量分别是6,3,3,4,5,4,3(单位:本),小明该月阅读了x本课外书,将x添加到前面这组数据后,这列数的中位数不变,则x可能是( )
A.1 B.2 C.3 D.4
3.同学A在计算方差时使用了一个不完整的计算公式,,同学B则根据这个公式计算出了下列结果,同学A却说,同学B有一个结论错了,你认为错误的是( )
A. B. C.众数为3 D.中位数为3
4.如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 185 180 185 180
方差 3.6 3.6 7.4 8.1
根据表数据,从中选择一名成绩好且发挥稳定的参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
5.乡村医生李医生在对本村老年人进行年度免费体检时,发现张奶奶血压偏高,为了准确诊断,随后7天,李医生每天定时为张奶奶测量血压,测得数据如下表:
测量时间 第1天 第2天 第3天 第4天 第5天 第6天 第7天
收缩压(毫米汞柱) 151 148 140 139 140 136 140
舒张压(毫米汞柱) 90 92 88 88 90 80 88
对收缩压,舒张压两组数据分别进行统计分析,其中错误的是( )
A.收缩压的中位数为139 B.舒张压的众数为88
C.收缩压的平均数为142 D.舒张压的方差为
6.某企业生产厚度为的精密零件,为严把质量关,分别从A、B两车间随机抽出了50个精密零件,测量厚度,并将数据处理后制成如下表格,根据表中信息判断,下列说法错误的是( )
个数 平均厚度 厚度的方差
A车间 50
B车间 50
A.A、B两车间被抽出精密零件的平均厚度相同
B.本次采用的调查方式是抽样调查
C.被抽取的100个零件的厚度是本次调查的样本
D.B车间精密零件的厚度比A车间精密零件的厚度波动大
7.为了减轻学生课外作业负担,数学老师准备按照学生每天课外作业完成量(完成题目数量)实行分档布置作业.作业量分档递增,计划使第一档、第二档和第三档的作业量分别覆盖全校学生,和,为合理确定各档之间的界限,随机抽查了该校500名学生过去一段时间每天课外作业完成量的平均数(单位:个),并绘制了如下统计图(每组不包含最小值,包含最大值).下面四个推断合理的是( )
A.每天课外作业完成量不超过15个题的该校学生按第二档布置作业
B.每天课外作业完成量超过21个的该校学生按第三档布置作业
C.该校学生每天课外作业完成量的平均数不超过18个
D.该校学生每天课外作业完成量的中位数在15~18个之间
8.已知一组数据,,的方差是,则新的一组数据,,的方差是( )
A. B. C. D.
9.甲、乙、丙三位选手各10次射击,成绩的平均数均为93环,方差(单位:环)依次分别为0.026、0.015、0.032,则射击成绩最稳定的选手是____________(填“甲”、“乙”、“丙”中的一个).
10.跳远运动员小李在一次训练中,先跳了6次的成绩如下:,,,,,(单位:m),这六次成绩的平均数为,方差为.如果小李再跳一次,成绩为(单位:m),则小李这7次跳远成绩与前6次的成绩相比较,其方差___________(填“变大”或“变小”或“不变”)
11.学校抽查了30名学生参加学雷锋社会实践”活动的次数,并根据数据绘制成了条形统计图,则30名学生参加活动的次数的中位数是___________.
12.数学老师布置了10道选择题作为课堂练习,课代表将全班同学的答题情况绘制成了如图的统计图,根据统计图,全班每位同学答对的题数所组成的一组数据的中位数为m道,众数为n道,则_______.
13.2022年3月25日,教育部印发《务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校为了解该校学生一周的课外劳动情况,随机抽取部分学生调查了他们一周的课外劳动时间,并用得到的数据绘制成如下不完整的统计图表:
(1)统计表中的__________,__________,__________;
(2)被抽样调查的同学劳动时间的众数是__________,中位数是__________;
(3)请将条形图补充完整;
(4)求所有被调查同学的平均劳动时间.
14.为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如图所示的统计图表.
甲、乙射击成绩折线图
甲、乙射击成绩统计表
平均数 中位数 方差
甲 7 _____ 4
乙 _____ _____ 5.4
(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果甲选手又射靶一次,射中了7环,和之前的10次成绩的数据结合后,甲选手射击成绩的平均数______;中位数______;方差______.(填“变大”“变小”或“不变”)
答案以及解析
1.答案:A
解析:观察表中可知,1.65出现了5次,次数最多,
运动员的成绩的众数为:1.65米.
将表中的数据按照从小到大的顺序排列如下:
1.50,1.50,1.60,1.60,1.60,1.65,1.65,1.65,1.65,1.65,1.70,1.70,1.70,1.70,1.75
运动员的成绩的中位数是1.65米.
故选:A.
2.答案:D
解析:将这组数据从小到大排列为:3,3,3,4,4,5,6,则中位数为4,
增加一个数x后,这列数的中位数仍不变,
则这组数据从小到大排列为:3,3,3,4,x,4,5,6,或3,3,3,x,4,4,5,6,
,
解得.
故选:D.
3.答案:A
解析:
平均数是3,
,
,故B不符合题意;
,故A符合题意;
从小到大排列为:1,2,3,3,6,
样本众数是3,故选项C不合题意;
中位数为3,故选项D不符合题意;
故选:A.
4.答案:A
解析:∵=>=,
∴从甲和丙中选择一人参加比赛,
∵,
∴选择甲参赛,
故选A.
5.答案:A
解析:把收缩压的数据按照从小到大的顺序排列为:
136,139,140,140,140,148,151;
排在最中间的数据是140,可得中位数为140,故A符合题意;
收缩压的平均数为:,故C不符合题意;
舒张压的数据中88出现3次,所以舒张压的数据的众数为88,故D不符合题意;
舒张压的平均数为:,
舒张压的方差为:;故D不符合题意;
故选A.
6.答案:D
解析:A、A、B两车间被抽出精密零件的平均厚度相同是正确的,不符合题意∶
B、两个车间的零件数量较多,不能采用普查,要用抽样调查是正确的,不符合题意;
C、被抽取的100个零件的厚度是本次调查的样本是正确的,不符合题意;
D、,A车间精密零件的厚度比A车间精密零件的厚度波动大,原说法错误,符合题意.
故选:D.
7.答案:C
解析:A选项,由统计图可得该校500名学生过去一段时间每天课外作业完成量的平均数不超过15个题的有(名),,故每天课外作业完成量不超过15个题的该校学生按第一档布置作业,故该选项错误,不符合题意;B选项,因为该校500名学生过去一段时间每天课外作业完成量的平均数超过21个题的有(名),,故此选项错误,不符合题意;C选项,通过计算加权平均数得,该校学生每天课外作业完成量的平均数不超过18个,正确,符合题意;D选项,因为按从小到大的顺序排列的500个数据的中位数是第250和251个数据的平均数,由统计图可知,第250和251个数据分别在9~12和12~15之间,所以其中位数应该在9~15之间,故此选项错误,不符合题意.故选C.
8.答案:A
解析:设这组数据,,的平均数为,方差,则另一组新数据,,的平均数为,方差为,
,
=
=
故选:A.
9.答案:乙
解析:甲、乙、丙三位选手各10次射击,
方差依次分别为:0.026、0.015、0.032,.
则射击成绩最稳定的选手是乙.
10.答案:变小
解析:小李再跳一次,成绩为,
这组数据的平均数是(m),
这7次跳远成绩的方差是:
,
,
方差变小,
故答案为:变小.
11.答案:3
解析:这组数据共有个,按顺序排列后位于中间的是第15和16个数,这两个数都是3,
中位数为:.
即30名学生参加活动的次数的中位数是3,
故答案为:3.
12.答案:17
解析:由统计图可知,在这组数据中7出现了4次,8出现了20次,9出现了18次,10出现了8次,所以8是出现次数最多的数据,所以这组数据的众数是8道.因为这组数据共有(个),所以中位数是第25个数据和第26个数据的平均数.因为这两个数据都是9,所以这组数据的中位数是9道,所以.
13.答案:(1)100,50,0.08
(2)1.5,1.5
(3)见解析
(4)所有被调查同学的平均劳动时间是1.27小时
解析:(1),,.
故答案为:100,50,0.08;
(2)被抽样调查的同学劳动时间数据中,
出现的次数最多的是1.5,故这组数据的众数为1.5;
参与调查的学生人数一共有100人,将他们的劳动时间从低到高排列,处在第50名和第51名的劳动时间分别为1.5和1.5,
中位数为.
故答案为:1.5,1.5;
(3)补画条形统计图如下:
(4)(小时).
答:所有被调查同学的平均劳动时间是1.27小时.
14.答案:(1)见解析
(2)甲应胜出;理由:甲、乙二人射击成绩的平均数相同,而甲射击成绩的方差小于乙,说明甲发挥得更稳定,所以甲应胜出
(3)不变;不变;变小
解析:(1)根据折线统计图得:
甲的射击成绩为9,6,7,6,2,7,7,?,8,9,平均数为7环,
则甲第八环成绩为(环),
所以甲的10次成绩为:9,6,7,6,2,7,7,9,8,9,
把这些数从小到大排列为2,6,6,7,7,7,8,9,9,9,
则中位数是:(环),
乙的射击成绩为:2,4,6,8,7,7,8,9,9,10,
则平均数为:(环),
把这些数从小到大排列为2,4,6,7,7,8,8,9,9,10,
则中位数是:(环),
补统计表如下:
平均数 中位数 方差
甲 7 7 4
乙 7 7.5 5.4
补全折线统计图如下:
(2)甲应胜出;
理由:甲、乙二人射击成绩的平均数相同,而甲射击成绩的方差小于乙,说明甲发挥得更稳定,所以甲应胜出;
(3)由(1)知平均数为7,增加1次射中7环后,则平均数不变;
中位数是第6个数,仍然是7环不变;
方差变小,理由是乙的新方差的分子的值不变,但是分母的值变大了,故新方差的值变小了;
故答案为:不变;不变;变小.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
