上海市松江区2016届九年级上学期期末教学质量监控数学试题
文档属性
| 名称 | 上海市松江区2016届九年级上学期期末教学质量监控数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 407.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-22 12:48:43 | ||
图片预览


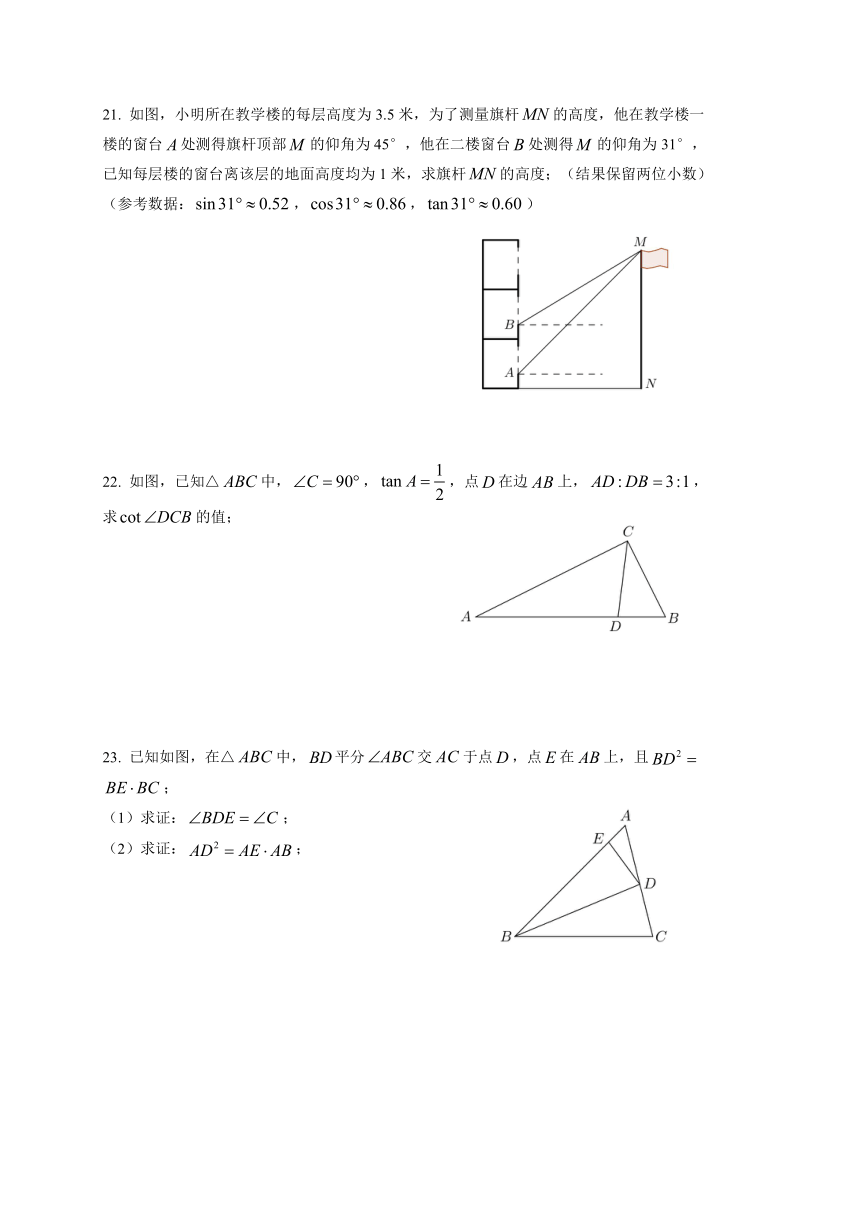


文档简介
松江区2016届九年级上学期期末教学质量监控
数学试题
一. 选择题
1. 如果两个相似三角形的面积比是,那么它们的周长比是( )
A. ; B. ; C. ; D. ;
2. 下列函数中,属于二次函数的是( )
A. ; B. ;
C. ; D. ;
3. 在Rt△中,,,,则下列结论正确的是( )
A. ; B. ; C. ; D. ;
4. 若四边形的对角线交于点,且有,则以下结论正确的是( )
A. ; B. ; C. ; D. ;
5. 如果二次函数()的图像
如图所示,那么( )
A. ,,;
B. ,,;
C. ,,;
D. ,,;
6. 是△一边上的一点(不与、、重合),过点的一条直线截△,
如果截得的三角形与△相似,我们称这条直线为过点的△的“相似线”
Rt△中,,,当点为的中点时,过点的△的
“相似线最多有几条?( )
A. 1条; B. 2条; C. 3条; D. 4条;
二. 填空题
7. 若,且,则 ;
8. 已知线段,,那么线段、的比例中项等于 ;
9. 二次函数的图像与轴的交点坐标为 ;
10. 在Rt△中,,如果,,那么 ;
11. 一位运动员投掷铅球,如果铅球运行时离地面的高度为(米)关于水平距离(米)的函数解析式为,那么铅球运动过程中最高点离地面的距离为
米;
12. 如图,直线∥∥,,,那么的值是 ;
13. 在一个斜坡上前进5米,水平高度升高了1米,则该斜坡坡度 ;
14. 若点、是二次函数图像上的两点,那么与的大小关系是 (填、或);
15. 将抛物线沿轴向右平移2个单位后所得抛物线的解析式是 ;
16. 如图,已知∥,且经过△的重心,若,那么等于
;
17. 已知二次函数的图像经过、两点,则该二次函数的图像对称轴为直线 ;
18. 已知在△中,,,,点是边上一点,将△沿着直线翻折,点落在直线上的点处,则 ;
三. 解答题
19. 已知抛物线经过点,顶点为;
(1)求抛物线的表达式;
(2)设抛物线对称轴与轴交于点,连接、,求△的面积;
20. 如图,已知平行四边形,点、是边、的中点,设,;
(1)求向量(用向量、表示);
(2)在图中求作向量在、方向上的分向量;
(不要求写作法,但要指出所作图中表示结论的向量)
21. 如图,小明所在教学楼的每层高度为3.5米,为了测量旗杆的高度,他在教学楼一
楼的窗台处测得旗杆顶部的仰角为45°,他在二楼窗台处测得的仰角为31°,
已知每层楼的窗台离该层的地面高度均为1米,求旗杆的高度;(结果保留两位小数)
(参考数据:,,)
22. 如图,已知△中,,,点在边上,,
求的值;
23. 已知如图,在△中,平分交于点,点在上,且
;
(1)求证:;
(2)求证:;
24. 如图,已知抛物线与轴交于、两点,与轴交于点,是坐
标原点,已知点的坐标是,;
(1)求该抛物线的函数表达式;
(2)点在轴上方的抛物线上,且,求点的坐标;
(3)点是轴上一动点,若以、、为顶点的三角形与△相似,求出符合条
件的点的坐标;
25. 已知,等腰梯形中,∥,,,,
点是对角线上的一个动点,且,分别交射线和射线于点
和点;
(1)如图1,当点、重合时,求的长;
(1)如图2,当点在的延长线上时,设,,求关于的函数解
析式,并写出它的定义域;
(3)当线段时,求的值;
2016年松江区中考数学一模卷
一、选择题
1.D 2.C 3.B 4.A 5.A 6.C
二、填空题
7.8 8.4 9.(0,3) 10.6 11.3 12.4 13.
14. 15. 16.4 17.x=2 18.
三、解答题
19.【解】(1)∵抛物线经过点,
∴,……………………………………………………(2分)
解得,……………………………………………………………(2分)
∴所求抛物线的表达式为;…………………………(1分)
(2)作AH⊥BM于点H,
∵由抛物线解析式可得,
点M的坐标为,点B的坐标为(2,0),………………………(2分)
∴BM=1,…………………………………………………………………(1分)
∵对称轴为直线,∴AH=3,……………………………………(1分)
∴△ABM的面积.……………………………………(1分)
第19题图
20.【解】(1)方法一:∵四边形ABCD是平行四边形,
∴ABDC,ADBC,AB=DC,AD=BC,……………………………(1分)
∵,,
∴,,…………………………(1分)
∵点M、N分别为DC、BC的中点,
,,…………(2分)
,……………………………………(1分)
方法二: ∵,,
,……………………………………………………(2分)
∵点M、N分别为DC、BC的中点,
,………………………………………………………(3分)
(2)作图.………………………………………………………………(4分)
结论:、是向量分别在、方向上的分向量.………(1分)
第20题图
21.【解】过点M的水平线交直线AB于点H,
由题意,得∠AMH=∠MAH=45°,,AB=3.5,………………(3分)
设MH=x,则AH=x, , ……………………………(2分)
,…………………………………(3分)
x=8.75,…………………………………………………………………………(1分)
则旗杆高度(米)
答:旗杆MN的高度度约为9.75米.…………………………………………(1分)
22.【解】过D点作DH⊥BC于点H,…………………………………………(1分)
∵
∴DHAC,
∵
∴ ……(2分)
∵设DH=x,则AC=4 x , ……………………………………………………(2分)
∵,
∴ , …………………………………………………………………(2分)
∵
∵CH= , ……………………………………………………………………(2分)
∴.…………………………………(1分)
第22题图
23.【证明】
(1)∵BD平分∠ABC,
∴∠ABD=∠CBD,……………………………………………………………(1分)
∵,
,…………………………………………………………………(2分)
∴△EBD∽△DBC,……………………………………………………………(2分)
∴∠BDE=∠C;…………………………………………………………………(1分)
(2) ∵∠BDE=∠C,
∠DBC+∠C=∠BDE+∠ADE,………………………………………………(1分)
∴∠DBC =∠ADE,……………………………………………………………(1分)
∵∠ABD=∠CBD,
∴∠ABD=∠ADE,………………………………………………………………(1分)
∴,…………………………………………………………(1分)
∴,
即.……………………………………………………………(2分)
第23题图
24.【解】(1)∵抛物线与y轴交于点C,
点C的坐标为,∴,
∵,
OA=1,即点A的坐标为,…(1分)
又点,
a=1,b =2, ………………………………(2分)
抛物线的函数表达式是;……………………………(1分)
(2)∵∠PAB=∠CAB,
∴,……………………………………………(1分)
∵点P在x轴上方,设点P的横坐标为x,则点P的纵坐标为,
,得x=1(舍去)或x=6,……………………(2分)
当x=6时,y=21,
∴点P的坐标为(6,21); …………………………………………………(1分)
(3)设点D的坐标为,
易得为∠ABC=45°的锐角三角形,所以△DCB也是锐角三角形,
∴点D在点C的上方, …………………………………………………………(1分)
∴∠DCB=45°,
∴∠ABC=∠DCB,
AB=4,BC=,DC=y+3, ………………………………………………(1分)
①如果则,
∴y=1,即点D(0,1), ………………………………………………………(1分)
②如果则,
∴y=,即点D(0,). ……………………………………………………(1分)
第24题图
25.【解】(1)作AH⊥BC于点H,
∵∠B=∠BCD=45°,AD=3,BC=9,
∴BH=AH=3,AB=,CH=6,
∴AC=,………………………………(1分)
∵ADBC,
∴∠DAP=∠ACB,又∠APE=∠B,
∴,……………………………………………………………(2分)
∴,即,
∴;…………………………………………………………………(1分)
第25题图1
(2)∵∠DAP=∠ACB,∠APE=∠B,
∴,……………………(1分)
∴,
∴,………………………………………………………………(1分)
∴, ……………………………………………………………(1分)
定义域:; ……………………………………………(1分)
(3)方法一:①当点G在线段CD上时,
作DMEP交AC于点M,
由(1)得AM=,∴CM=,……………………………………(1分)
DG=,CD=AB=,
∴CG=,
,
∴PM=,……………………………………………………………………(1分)
由得DE=,………………………………………………………(1分)
∴AE=,………………………………………………………………(1分)
第25题图2
②当点G在CD的延长线上时,
同①可得DE=, ………………………………………………………………(1分)
∴AE=;………………………………………………………………(1分)
第25题图3
方法二:当点G在线段CD上时,
ADBC,
∴∠EAC=∠ACB,
∴∠EDC =∠BCD,
∠B=∠BCD=45°,∠EDC=∠B,
∠APE=∠B,
∴∠APE=∠ EDC,
∴∠EGD=∠EAP,
∴∠EGD=∠ACB,
∴△ACB∽△EGD,……………………………………………………………(1分)
∴ , ∴,
∴得DE=,……………………………………………………………………(1分)
∴AE=,………………………………………………………………(1分)
②当点G在CD的延长线上时,
, ……………………………………………………………(1分)
同①可得DE=,…………………………………………………………………(1分)
∴AE=.…………………………………………………………………(1分)
第25题图4
数学试题
一. 选择题
1. 如果两个相似三角形的面积比是,那么它们的周长比是( )
A. ; B. ; C. ; D. ;
2. 下列函数中,属于二次函数的是( )
A. ; B. ;
C. ; D. ;
3. 在Rt△中,,,,则下列结论正确的是( )
A. ; B. ; C. ; D. ;
4. 若四边形的对角线交于点,且有,则以下结论正确的是( )
A. ; B. ; C. ; D. ;
5. 如果二次函数()的图像
如图所示,那么( )
A. ,,;
B. ,,;
C. ,,;
D. ,,;
6. 是△一边上的一点(不与、、重合),过点的一条直线截△,
如果截得的三角形与△相似,我们称这条直线为过点的△的“相似线”
Rt△中,,,当点为的中点时,过点的△的
“相似线最多有几条?( )
A. 1条; B. 2条; C. 3条; D. 4条;
二. 填空题
7. 若,且,则 ;
8. 已知线段,,那么线段、的比例中项等于 ;
9. 二次函数的图像与轴的交点坐标为 ;
10. 在Rt△中,,如果,,那么 ;
11. 一位运动员投掷铅球,如果铅球运行时离地面的高度为(米)关于水平距离(米)的函数解析式为,那么铅球运动过程中最高点离地面的距离为
米;
12. 如图,直线∥∥,,,那么的值是 ;
13. 在一个斜坡上前进5米,水平高度升高了1米,则该斜坡坡度 ;
14. 若点、是二次函数图像上的两点,那么与的大小关系是 (填、或);
15. 将抛物线沿轴向右平移2个单位后所得抛物线的解析式是 ;
16. 如图,已知∥,且经过△的重心,若,那么等于
;
17. 已知二次函数的图像经过、两点,则该二次函数的图像对称轴为直线 ;
18. 已知在△中,,,,点是边上一点,将△沿着直线翻折,点落在直线上的点处,则 ;
三. 解答题
19. 已知抛物线经过点,顶点为;
(1)求抛物线的表达式;
(2)设抛物线对称轴与轴交于点,连接、,求△的面积;
20. 如图,已知平行四边形,点、是边、的中点,设,;
(1)求向量(用向量、表示);
(2)在图中求作向量在、方向上的分向量;
(不要求写作法,但要指出所作图中表示结论的向量)
21. 如图,小明所在教学楼的每层高度为3.5米,为了测量旗杆的高度,他在教学楼一
楼的窗台处测得旗杆顶部的仰角为45°,他在二楼窗台处测得的仰角为31°,
已知每层楼的窗台离该层的地面高度均为1米,求旗杆的高度;(结果保留两位小数)
(参考数据:,,)
22. 如图,已知△中,,,点在边上,,
求的值;
23. 已知如图,在△中,平分交于点,点在上,且
;
(1)求证:;
(2)求证:;
24. 如图,已知抛物线与轴交于、两点,与轴交于点,是坐
标原点,已知点的坐标是,;
(1)求该抛物线的函数表达式;
(2)点在轴上方的抛物线上,且,求点的坐标;
(3)点是轴上一动点,若以、、为顶点的三角形与△相似,求出符合条
件的点的坐标;
25. 已知,等腰梯形中,∥,,,,
点是对角线上的一个动点,且,分别交射线和射线于点
和点;
(1)如图1,当点、重合时,求的长;
(1)如图2,当点在的延长线上时,设,,求关于的函数解
析式,并写出它的定义域;
(3)当线段时,求的值;
2016年松江区中考数学一模卷
一、选择题
1.D 2.C 3.B 4.A 5.A 6.C
二、填空题
7.8 8.4 9.(0,3) 10.6 11.3 12.4 13.
14. 15. 16.4 17.x=2 18.
三、解答题
19.【解】(1)∵抛物线经过点,
∴,……………………………………………………(2分)
解得,……………………………………………………………(2分)
∴所求抛物线的表达式为;…………………………(1分)
(2)作AH⊥BM于点H,
∵由抛物线解析式可得,
点M的坐标为,点B的坐标为(2,0),………………………(2分)
∴BM=1,…………………………………………………………………(1分)
∵对称轴为直线,∴AH=3,……………………………………(1分)
∴△ABM的面积.……………………………………(1分)
第19题图
20.【解】(1)方法一:∵四边形ABCD是平行四边形,
∴ABDC,ADBC,AB=DC,AD=BC,……………………………(1分)
∵,,
∴,,…………………………(1分)
∵点M、N分别为DC、BC的中点,
,,…………(2分)
,……………………………………(1分)
方法二: ∵,,
,……………………………………………………(2分)
∵点M、N分别为DC、BC的中点,
,………………………………………………………(3分)
(2)作图.………………………………………………………………(4分)
结论:、是向量分别在、方向上的分向量.………(1分)
第20题图
21.【解】过点M的水平线交直线AB于点H,
由题意,得∠AMH=∠MAH=45°,,AB=3.5,………………(3分)
设MH=x,则AH=x, , ……………………………(2分)
,…………………………………(3分)
x=8.75,…………………………………………………………………………(1分)
则旗杆高度(米)
答:旗杆MN的高度度约为9.75米.…………………………………………(1分)
22.【解】过D点作DH⊥BC于点H,…………………………………………(1分)
∵
∴DHAC,
∵
∴ ……(2分)
∵设DH=x,则AC=4 x , ……………………………………………………(2分)
∵,
∴ , …………………………………………………………………(2分)
∵
∵CH= , ……………………………………………………………………(2分)
∴.…………………………………(1分)
第22题图
23.【证明】
(1)∵BD平分∠ABC,
∴∠ABD=∠CBD,……………………………………………………………(1分)
∵,
,…………………………………………………………………(2分)
∴△EBD∽△DBC,……………………………………………………………(2分)
∴∠BDE=∠C;…………………………………………………………………(1分)
(2) ∵∠BDE=∠C,
∠DBC+∠C=∠BDE+∠ADE,………………………………………………(1分)
∴∠DBC =∠ADE,……………………………………………………………(1分)
∵∠ABD=∠CBD,
∴∠ABD=∠ADE,………………………………………………………………(1分)
∴,…………………………………………………………(1分)
∴,
即.……………………………………………………………(2分)
第23题图
24.【解】(1)∵抛物线与y轴交于点C,
点C的坐标为,∴,
∵,
OA=1,即点A的坐标为,…(1分)
又点,
a=1,b =2, ………………………………(2分)
抛物线的函数表达式是;……………………………(1分)
(2)∵∠PAB=∠CAB,
∴,……………………………………………(1分)
∵点P在x轴上方,设点P的横坐标为x,则点P的纵坐标为,
,得x=1(舍去)或x=6,……………………(2分)
当x=6时,y=21,
∴点P的坐标为(6,21); …………………………………………………(1分)
(3)设点D的坐标为,
易得为∠ABC=45°的锐角三角形,所以△DCB也是锐角三角形,
∴点D在点C的上方, …………………………………………………………(1分)
∴∠DCB=45°,
∴∠ABC=∠DCB,
AB=4,BC=,DC=y+3, ………………………………………………(1分)
①如果则,
∴y=1,即点D(0,1), ………………………………………………………(1分)
②如果则,
∴y=,即点D(0,). ……………………………………………………(1分)
第24题图
25.【解】(1)作AH⊥BC于点H,
∵∠B=∠BCD=45°,AD=3,BC=9,
∴BH=AH=3,AB=,CH=6,
∴AC=,………………………………(1分)
∵ADBC,
∴∠DAP=∠ACB,又∠APE=∠B,
∴,……………………………………………………………(2分)
∴,即,
∴;…………………………………………………………………(1分)
第25题图1
(2)∵∠DAP=∠ACB,∠APE=∠B,
∴,……………………(1分)
∴,
∴,………………………………………………………………(1分)
∴, ……………………………………………………………(1分)
定义域:; ……………………………………………(1分)
(3)方法一:①当点G在线段CD上时,
作DMEP交AC于点M,
由(1)得AM=,∴CM=,……………………………………(1分)
DG=,CD=AB=,
∴CG=,
,
∴PM=,……………………………………………………………………(1分)
由得DE=,………………………………………………………(1分)
∴AE=,………………………………………………………………(1分)
第25题图2
②当点G在CD的延长线上时,
同①可得DE=, ………………………………………………………………(1分)
∴AE=;………………………………………………………………(1分)
第25题图3
方法二:当点G在线段CD上时,
ADBC,
∴∠EAC=∠ACB,
∴∠EDC =∠BCD,
∠B=∠BCD=45°,∠EDC=∠B,
∠APE=∠B,
∴∠APE=∠ EDC,
∴∠EGD=∠EAP,
∴∠EGD=∠ACB,
∴△ACB∽△EGD,……………………………………………………………(1分)
∴ , ∴,
∴得DE=,……………………………………………………………………(1分)
∴AE=,………………………………………………………………(1分)
②当点G在CD的延长线上时,
, ……………………………………………………………(1分)
同①可得DE=,…………………………………………………………………(1分)
∴AE=.…………………………………………………………………(1分)
第25题图4
同课章节目录
