2024-2025学年广东省深圳市福田外国语学校九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年广东省深圳市福田外国语学校九年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 158.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-07 14:11:16 | ||
图片预览



文档简介
2024-2025学年广东省深圳市福田外国语学校九年级(上)开学
数学试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在数学活动课中,同学们利用几何画板绘制出了下列曲线,其中既是轴对称图形又是中心对称图形的是( )
A. 三叶玫瑰线 B. 笛卡尔心形线
C. 蝴蝶曲线 D. 四叶玫瑰线
2.下列各等式从左边到右边的变形中,是因式分解的是( )
A. B.
C. D.
3.已知点在第二象限,则的取值范围在数轴上表示正确的是( )
A. B. C. D.
4.小明在解关于的分式方程时,发现墨水不小心把其中一个数字污染了,翻看答案上说此方程有增根无解,则被污染的数字为( )
A. B. C. D.
5.下面是嘉嘉作业本上的一道习题及解答过程:
已知:如图,中,,平分的外角,点是的中点,连接并延长交于点,连接.
求证:四边形是平行四边形.
证明:,.
,,,
______.
又,,
≌______.
四边形是平行四边形.
若以上解答过程正确,,应分别为( )
A. , B. ,
C. , D. ,
6.某单位向一所希望小学赠送了件文具,现用、两种不同的包裝箱进行包装,已知每个型包装箱比型包装箱多装件文具,单独使用型包装箱比单独使用型包装箱可少用个,设型包装箱每个可以装件文具,根据题意列方程为( )
A. B.
C. D.
7.如图,在中,,过点作,连接与交于点,
是边的中点,,若,,则的长为( )
A. B. C. D.
8.如图,在四边形中,,,,,,则对角线的长是( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
9.分解因式: .
10.若代数式在实数范围内有意义,则的取值范围是______.
11.如图所示,一次函数与的交点坐标为,则不等式的解集为______.
12.如图,为中的外角平分线,于,为中点,,,则长为______.
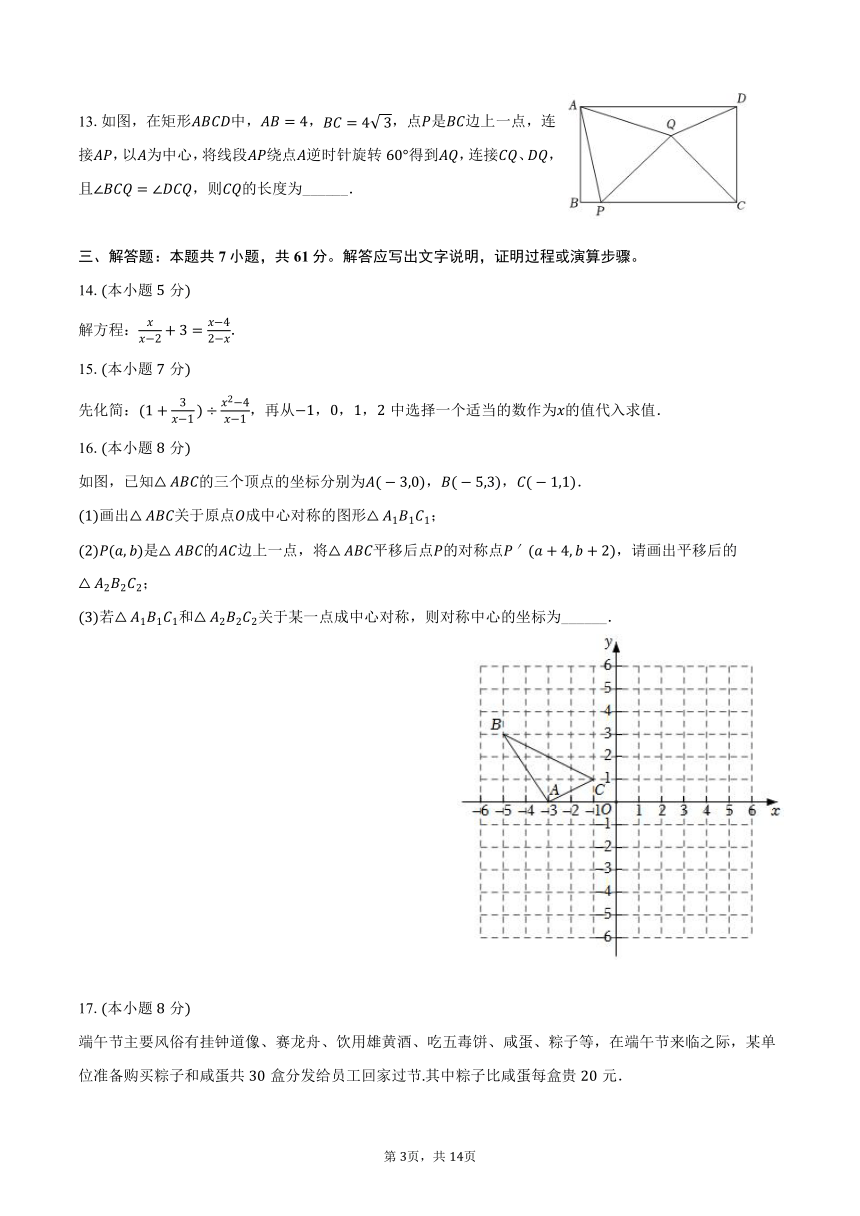
13.如图,在矩形中,,,点是边上一点,连接,以为中心,将线段绕点逆时针旋转得到,连接、,且,则的长度为______.
三、解答题:本题共7小题,共61分。解答应写出文字说明,证明过程或演算步骤。
14.本小题分
解方程:.
15.本小题分
先化简:,再从,,,中选择一个适当的数作为的值代入求值.
16.本小题分
如图,已知的三个顶点的坐标分别为,,.
画出关于原点成中心对称的图形;
是的边上一点,将平移后点的对称点,请画出平移后的;
若和关于某一点成中心对称,则对称中心的坐标为______.
17.本小题分
端午节主要风俗有挂钟道像、赛龙舟、饮用雄黄酒、吃五毒饼、咸蛋、粽子等,在端午节来临之际,某单位准备购买粽子和咸蛋共盒分发给员工回家过节其中粽子比咸蛋每盒贵元.
若用元购买咸蛋与用元购买粽子的数量相同,求粽子和咸蛋每盒的价格;
在的条件下,若购买咸蛋数量不超过粽子数量的倍,如何购买才能使总费用最少?
18.本小题分
如图,在 中,点是对角线的中点某数学兴趣小组要在上找两个点,,使四边形为平行四边形,现总结出甲、乙两种方案如下:
甲方案 乙方案
在,上分别取点,,使得
作于点,于点
请回答下列问题:
选择其中一种方案,并证明四边形为平行四边形;
在的基础上,若,,则 的面积为______.
19.本小题分
如图,在四边形中,,顶点坐标分别为,,,,,动点从开始以每秒个单位长度的速度沿线段向运动,另一个动点以每秒个单位长度的速度从开始运动,、同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为秒.
请回答下列问题:
______, ______;
如图,若点沿折线向运动,
为何值时,,请说明理由;
为何值时,以点、和四边形的任意两个顶点为顶点的四边形是平行四边形,请说明理由;
如图,若点沿射线运动,当线段被平分时,直接写出点坐标为______.
20.本小题分
综合与实践
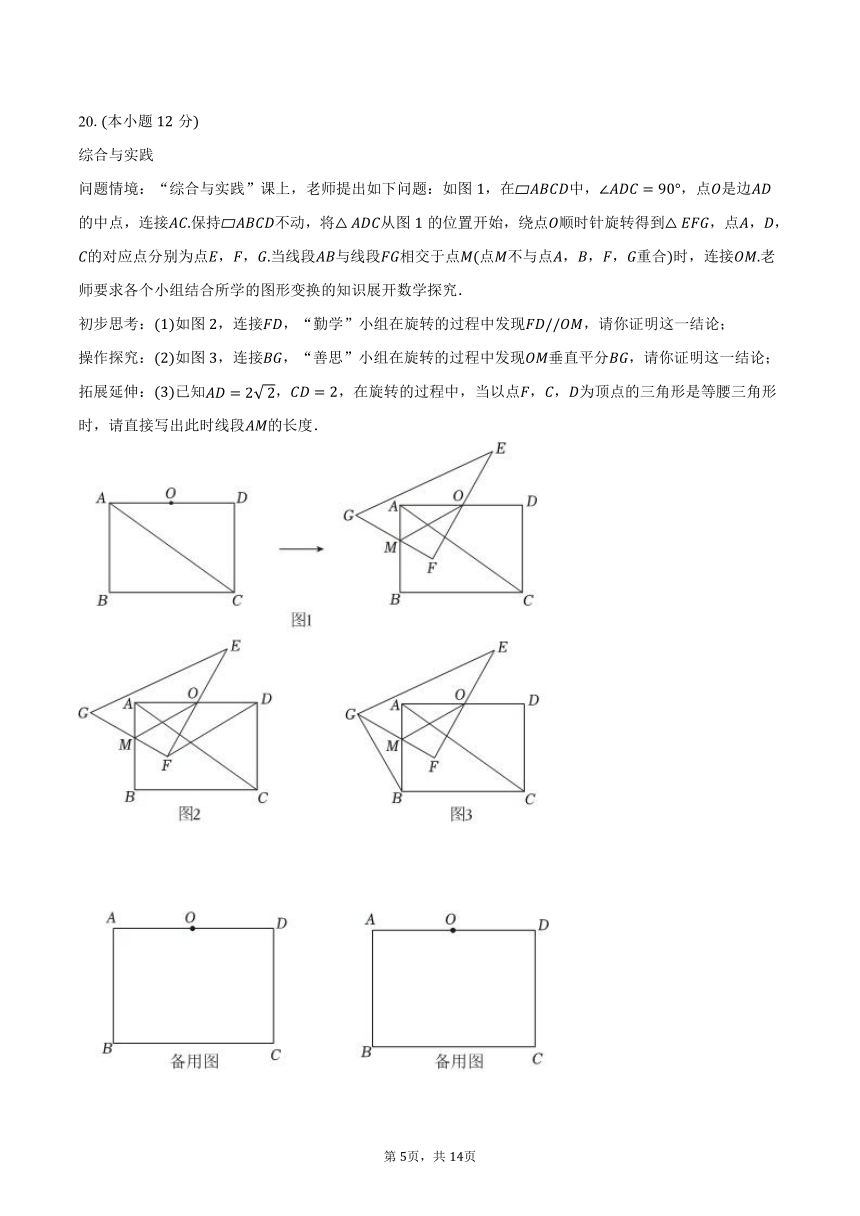
问题情境:“综合与实践”课上,老师提出如下问题:如图,在 中,,点是边的中点,连接保持 不动,将从图的位置开始,绕点顺时针旋转得到,点,,的对应点分别为点,,当线段与线段相交于点点不与点,,,重合时,连接老师要求各个小组结合所学的图形变换的知识展开数学探究.
初步思考:如图,连接,“勤学”小组在旋转的过程中发现,请你证明这一结论;
操作探究:如图,连接,“善思”小组在旋转的过程中发现垂直平分,请你证明这一结论;
拓展延伸:已知,,在旋转的过程中,当以点,,为顶点的三角形是等腰三角形时,请直接写出此时线段的长度.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.解:,
方程两边都乘,得,
解得:,
检验:当时,,
所以是增根,
即原方程无解.
15.解:
,
,,
或,
当时,分式
16.如图所示,即为所求;
如图所示,即为所求.
对称中心的坐标为.
故答案为.
17.解:设粽子每盒的价格为元,则咸蛋每盒的价格为元,
由题意得:,
解得:,
经检验,是原方程的解,且符合题意,
,
答:粽子每盒的价格为元,咸蛋每盒的价格为元;
设购买咸蛋为盒,则购买粽子为盒,
由题意得:,
解得:,
设总费用为元,
则,
,
随的增大而减小,
当时,最小,
此时,,
答:购买咸蛋盒,粽子盒时,总费用最少.
18.甲方案,证明:四边形是平行四边形,
,,
,
在和中,
,
≌,
,,
,,
,
,
四边形是平行四边形.
乙方案,证明:于点,于点,
,,
四边形是平行四边形,
,,
,
在和中,
,
≌,
,
四边形是平行四边形;
由得≌,
,
,
,
四边形是平行四边形,
,
,
19.,;
由题意知点运动过程中的坐标为,
,
是直角三角形,
,
,
,,
,
即或,
解得或舍去,
时,;
由题意,分两种情况,当时,时,
由题得当时,点在上运动,
若想,与四边形的任意两个顶点构成平行四边形,,
即且,
,,
,
;
当时,
根据题意,,
,
,,
,
;
当时,
,
;
故的值为或或;
设直线的解析式为,
代入,两点,
则,
得,
,
,
被平分,
的中点,
在线段上,
点纵坐标为,
,
,
,
点坐标为,
20.证明:如图,连接,,
将绕点顺时针旋转得到,
,,
,
,
,
点是边的中点,
,
.
四边形是平行四边形,
,
,
又,
,
,
在和中,
≌,
,
是的一个外角,
,
即,
,
;
证明:如图,延长交于点,
由知:≌,
,,
将绕点顺时针旋转得到,
,
四边形是平行四边形,
,
,
,
即,
,,,
,
垂直平分;
解:以点,,为顶点的三角形是等腰三角形,
或或,
当时,如图,过点作于,交于,过点作于,
则四边形、、均为矩形,
,,
,,点是边的中点,
,
,,
,
,
由旋转得,
又,
,
,
,
,
是等腰直角三角形,
,
;
当时,如图,连接,
由旋转得,
又,
≌,
,
,
,
即、、三点共线,
在和中,
,
≌,
,
设,
四边形是矩形,,,
,,
则,,
在中,,
,
解得:,
;
当时,如图,过点作于,
,,
,
在中,,
,
和均为等腰直角三角形,
,
,
,
,
四边形是矩形,
;
综上所述,线段的长度为或或.
第1页,共1页
数学试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在数学活动课中,同学们利用几何画板绘制出了下列曲线,其中既是轴对称图形又是中心对称图形的是( )
A. 三叶玫瑰线 B. 笛卡尔心形线
C. 蝴蝶曲线 D. 四叶玫瑰线
2.下列各等式从左边到右边的变形中,是因式分解的是( )
A. B.
C. D.
3.已知点在第二象限,则的取值范围在数轴上表示正确的是( )
A. B. C. D.
4.小明在解关于的分式方程时,发现墨水不小心把其中一个数字污染了,翻看答案上说此方程有增根无解,则被污染的数字为( )
A. B. C. D.
5.下面是嘉嘉作业本上的一道习题及解答过程:
已知:如图,中,,平分的外角,点是的中点,连接并延长交于点,连接.
求证:四边形是平行四边形.
证明:,.
,,,
______.
又,,
≌______.
四边形是平行四边形.
若以上解答过程正确,,应分别为( )
A. , B. ,
C. , D. ,
6.某单位向一所希望小学赠送了件文具,现用、两种不同的包裝箱进行包装,已知每个型包装箱比型包装箱多装件文具,单独使用型包装箱比单独使用型包装箱可少用个,设型包装箱每个可以装件文具,根据题意列方程为( )
A. B.
C. D.
7.如图,在中,,过点作,连接与交于点,
是边的中点,,若,,则的长为( )
A. B. C. D.
8.如图,在四边形中,,,,,,则对角线的长是( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
9.分解因式: .
10.若代数式在实数范围内有意义,则的取值范围是______.
11.如图所示,一次函数与的交点坐标为,则不等式的解集为______.
12.如图,为中的外角平分线,于,为中点,,,则长为______.
13.如图,在矩形中,,,点是边上一点,连接,以为中心,将线段绕点逆时针旋转得到,连接、,且,则的长度为______.
三、解答题:本题共7小题,共61分。解答应写出文字说明,证明过程或演算步骤。
14.本小题分
解方程:.
15.本小题分
先化简:,再从,,,中选择一个适当的数作为的值代入求值.
16.本小题分
如图,已知的三个顶点的坐标分别为,,.
画出关于原点成中心对称的图形;
是的边上一点,将平移后点的对称点,请画出平移后的;
若和关于某一点成中心对称,则对称中心的坐标为______.
17.本小题分
端午节主要风俗有挂钟道像、赛龙舟、饮用雄黄酒、吃五毒饼、咸蛋、粽子等,在端午节来临之际,某单位准备购买粽子和咸蛋共盒分发给员工回家过节其中粽子比咸蛋每盒贵元.
若用元购买咸蛋与用元购买粽子的数量相同,求粽子和咸蛋每盒的价格;
在的条件下,若购买咸蛋数量不超过粽子数量的倍,如何购买才能使总费用最少?
18.本小题分
如图,在 中,点是对角线的中点某数学兴趣小组要在上找两个点,,使四边形为平行四边形,现总结出甲、乙两种方案如下:
甲方案 乙方案
在,上分别取点,,使得
作于点,于点
请回答下列问题:
选择其中一种方案,并证明四边形为平行四边形;
在的基础上,若,,则 的面积为______.
19.本小题分
如图,在四边形中,,顶点坐标分别为,,,,,动点从开始以每秒个单位长度的速度沿线段向运动,另一个动点以每秒个单位长度的速度从开始运动,、同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为秒.
请回答下列问题:
______, ______;
如图,若点沿折线向运动,
为何值时,,请说明理由;
为何值时,以点、和四边形的任意两个顶点为顶点的四边形是平行四边形,请说明理由;
如图,若点沿射线运动,当线段被平分时,直接写出点坐标为______.
20.本小题分
综合与实践
问题情境:“综合与实践”课上,老师提出如下问题:如图,在 中,,点是边的中点,连接保持 不动,将从图的位置开始,绕点顺时针旋转得到,点,,的对应点分别为点,,当线段与线段相交于点点不与点,,,重合时,连接老师要求各个小组结合所学的图形变换的知识展开数学探究.
初步思考:如图,连接,“勤学”小组在旋转的过程中发现,请你证明这一结论;
操作探究:如图,连接,“善思”小组在旋转的过程中发现垂直平分,请你证明这一结论;
拓展延伸:已知,,在旋转的过程中,当以点,,为顶点的三角形是等腰三角形时,请直接写出此时线段的长度.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.解:,
方程两边都乘,得,
解得:,
检验:当时,,
所以是增根,
即原方程无解.
15.解:
,
,,
或,
当时,分式
16.如图所示,即为所求;
如图所示,即为所求.
对称中心的坐标为.
故答案为.
17.解:设粽子每盒的价格为元,则咸蛋每盒的价格为元,
由题意得:,
解得:,
经检验,是原方程的解,且符合题意,
,
答:粽子每盒的价格为元,咸蛋每盒的价格为元;
设购买咸蛋为盒,则购买粽子为盒,
由题意得:,
解得:,
设总费用为元,
则,
,
随的增大而减小,
当时,最小,
此时,,
答:购买咸蛋盒,粽子盒时,总费用最少.
18.甲方案,证明:四边形是平行四边形,
,,
,
在和中,
,
≌,
,,
,,
,
,
四边形是平行四边形.
乙方案,证明:于点,于点,
,,
四边形是平行四边形,
,,
,
在和中,
,
≌,
,
四边形是平行四边形;
由得≌,
,
,
,
四边形是平行四边形,
,
,
19.,;
由题意知点运动过程中的坐标为,
,
是直角三角形,
,
,
,,
,
即或,
解得或舍去,
时,;
由题意,分两种情况,当时,时,
由题得当时,点在上运动,
若想,与四边形的任意两个顶点构成平行四边形,,
即且,
,,
,
;
当时,
根据题意,,
,
,,
,
;
当时,
,
;
故的值为或或;
设直线的解析式为,
代入,两点,
则,
得,
,
,
被平分,
的中点,
在线段上,
点纵坐标为,
,
,
,
点坐标为,
20.证明:如图,连接,,
将绕点顺时针旋转得到,
,,
,
,
,
点是边的中点,
,
.
四边形是平行四边形,
,
,
又,
,
,
在和中,
≌,
,
是的一个外角,
,
即,
,
;
证明:如图,延长交于点,
由知:≌,
,,
将绕点顺时针旋转得到,
,
四边形是平行四边形,
,
,
,
即,
,,,
,
垂直平分;
解:以点,,为顶点的三角形是等腰三角形,
或或,
当时,如图,过点作于,交于,过点作于,
则四边形、、均为矩形,
,,
,,点是边的中点,
,
,,
,
,
由旋转得,
又,
,
,
,
,
是等腰直角三角形,
,
;
当时,如图,连接,
由旋转得,
又,
≌,
,
,
,
即、、三点共线,
在和中,
,
≌,
,
设,
四边形是矩形,,,
,,
则,,
在中,,
,
解得:,
;
当时,如图,过点作于,
,,
,
在中,,
,
和均为等腰直角三角形,
,
,
,
,
四边形是矩形,
;
综上所述,线段的长度为或或.
第1页,共1页
同课章节目录
