2024-2025学年福建省福州十二中九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年福建省福州十二中九年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 105.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-07 14:12:32 | ||
图片预览




文档简介
2024-2025学年福建省福州十二中九年级(上)开学数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.化简的结果是( )
A. B. C. D.
2.下列计算正确的是( )
A. B. C. D.
3.在中,,,,则的长为( )
A. B. C. D.
4.由下列各组线段围成的三角形中,是直角三角形的是( )
A. ,, B. ,, C. ,, D. ,,
5.甲、乙、丙、丁四名同学进行分钟跳绳测试,每人次分钟跳绳成绩的平均数都是个,方差分别是,,,,则这四名同学分钟跳绳成绩最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
6.将一元二次方程化为一元二次方程的一般形式,其中二次项系数为,一次项系数和常数项分别是( )
A. , B. , C. , D. ,
7.关于的一元二次方程有两个不相等的实数根,则的取值范围是( )
A. B. C. 且 D. 且
8.如图,在菱形中,,对角线,则菱形的面积是( )
A.
B.
C.
D.
9.下列有关一次函数的说法中,正确的是( )
A. 的值随着值的增大而增大 B. 函数图象与轴的交点坐标为
C. 当时, D. 函数图象经过第二、三、四象限
10.在平面直角坐标系中,点坐标为,点坐标为,则,之间距离的最小值为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.二次根式有意义,则的取值范围是______.
12.一组数据为,,,,则这组数据的方差是______.
13.如图,周长为菱形的对角线相交于点,为的中点,
连接则的长为______.
14.方程的两个实数根分别是,,则的值是______.
15.函数的图象如图所示,则关于的不等式的解集是______.
16.如图,平行四边形中,,,,,分别是边,上的动点,且,则的最小值为______.
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:.
18.本小题分
解下列方程:
;
.
19.本小题分
如图,在矩形中,,分别是,上的点,连接,,若,求证:.
20.本小题分
某校为了解学生在学校甲、乙超市的生活消费情况,各随机抽查了名学生某一周按周一至周五算的消费金额单位:元,并将数据进行收集、整理和分析下面给出了部分信息.
消费金额的频数分布表如下:
消费金额元
甲超市
乙超市
乙超市消费金额在这一组的是:
甲、乙两个超市消费金额的平均数、中位数、众数如表:
超市 平均数 中位数 众数
甲
乙
根据以上信息,回答下列问题:
求表中和的值;
若甲超市该周的学生消费人数为人,估计甲超市一个月按周算的学生消费总金额.
21.本小题分
已知:如图,在矩形中,是边上的点,连接.
尺规作图,以为边,为顶点作,交线段于点要求:基本作图,保留作图痕迹,不写作法,不下结论.
求证:四边形为平行四边形
22.本小题分
某商店计划采购甲、乙两种不同型号的电视机进行销售.知商店购进甲型电视机台,乙型电视机台,需要花费元.进甲型电视机台,乙型电视机台,需要花费元.
求该商店购进甲、乙两种型号的电视机的单价分别为多少元?
该商店购进甲、乙两种型号的电视机共台,且购买的甲型电视机的数量不多于乙型电视机数量的倍.甲型电视机的售价为元台,乙型电视机的售价为元台,全部卖出,问:应购进甲种型号的电视机多少台?才能使该商店销售甲、乙两种不同型号的电视机获得的总利润最大,最大总利润是多少?
23.本小题分
综合实践:阅读下列材料,解答问题.
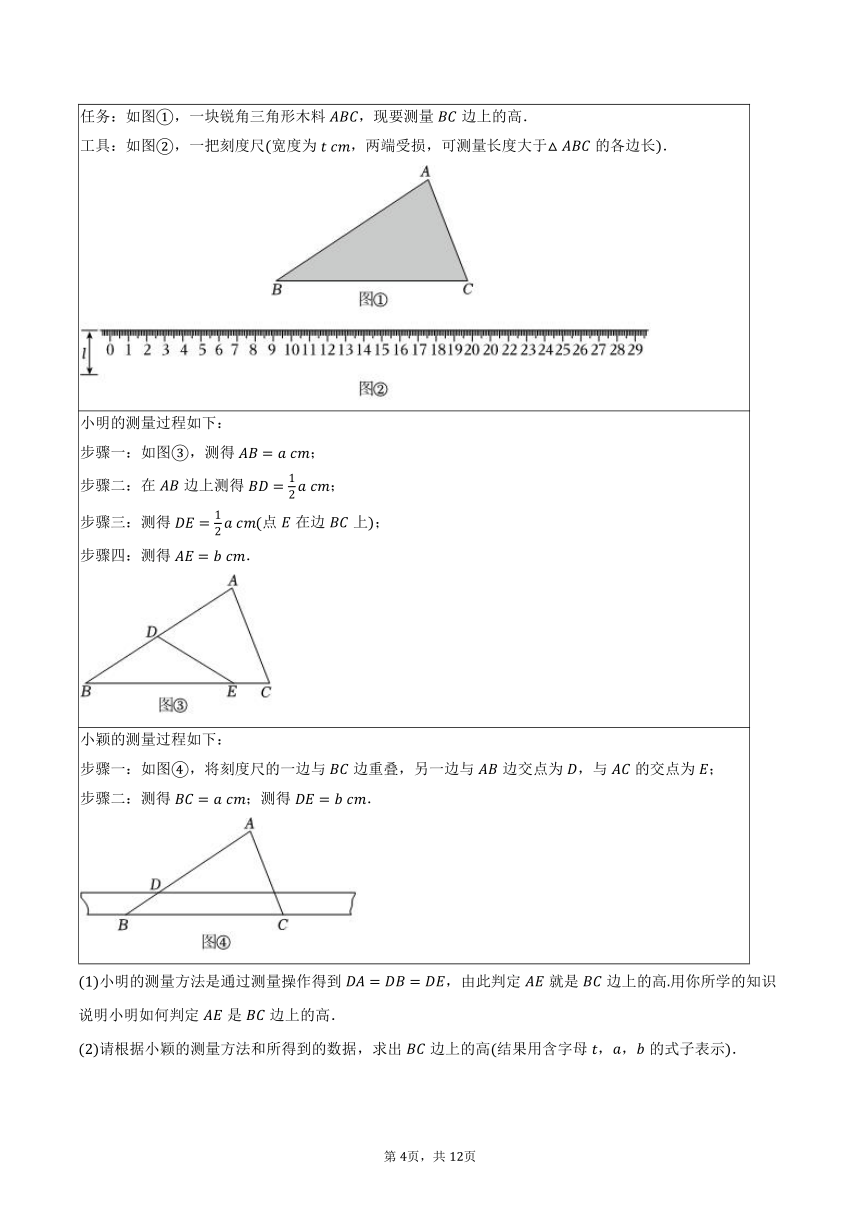
任务:如图,一块锐角三角形木料,现要测量边上的高.
工具:如图,一把刻度尺宽度为,两端受损,可测量长度大于的各边长.
小明的测量过程如下:
步骤一:如图,测得;
步骤二:在边上测得;
步骤三:测得点在边上;
步骤四:测得.
小颖的测量过程如下:
步骤一:如图,将刻度尺的一边与边重叠,另一边与边交点为,与的交点为;
步骤二:测得;测得.
小明的测量方法是通过测量操作得到,由此判定就是边上的高用你所学的知识说明小明如何判定是边上的高.
请根据小颖的测量方法和所得到的数据,求出边上的高结果用含字母,,的式子表示.
24.本小题分
在平面直角坐标系中,一次函数与为常数,且的图象相交于点.
当时,求点的坐标;
与的关系式记作函数,函数满足:当时,;当时,.
若函数的图象与轴总有两个不同的交点,求的取值范围;
在的条件下,当时,的最大值与最小值的差为,求的值.
25.本小题分
如图,在正方形中,点在边上不与点,重合,交对角线于点,交于点.
求证:.
若,,求的长.
如图,连接,,若,求正方形与的面积之比.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:原式
.
18.解:;
;
开方得:,
解得:,;
分解因式得:,
解得:,.
19.证明:四边形是矩形,
,,
在和中,
,
≌,
.
20.解:元,
第和第个数据为和,
元,
即表中的值为,的值为;
元,
答:估计甲超市一个月按周算的学生消费总金额为元.
21.解:如图所示,即为所求;
证明:四边形为矩形,
,,,,
,
在和中,
,
≌,
,
,
即,
四边形为平行四边形.
22.解:设商店购进甲种型号的电视机的单价为元,购进乙种型号的电视机的单价为元,
根据题意得:,
解得,
答:商店购进甲种型号的电视机的单价为元,购进乙种型号的电视机的单价为元;
设获得的总利润为元,购进甲种型号的电视机台,
购买的甲型电视机的数量不多于乙型电视机数量的倍,
,
解得,
根据题意得,
,
随的增大而增大,
时,取最大值,最大值为元,
答:购进甲种型号的电视机台,才能使该商店销售甲、乙两种不同型号的电视机获得的总利润最大,最大总利润是元.
23.证明:连接,以为圆心,长为半径作圆,
,
、在圆上,且是直径,
,即是边上的高;
判定是边上的高用到的几何知识是:直径所对的圆周角是直角;
解:过点作交于点,交于点,则,,设,则,
,即,
,
,
边上的高为.
24.解:当时,一次函数与为与,
,解得,
点的坐标为;
根据题意,得
,
解得,
点坐标为,
函数的图象与轴总有两个不同的交点,
;
由得,交点的横坐标为,即,
,,
由图象可知,当时,即当,且时,即,
时,,
时,,
时,,
,
时,,
当时,的最大值与最小值的差为,
,
解得符合题意,
当时,即,
时,函数的解析式为,
,
随着的增大而减小,
时,,
时,,
当时,的最大值与最小值的差为,
,
解得不合题意,舍去,
综上所述,的值为.
25.证明:连接,
四边形是正方形,
,,,
又,
≌,
,,
,且,
,
,
,
,
,
;
如图,过点作于,
,,
,
,
,,
,,
,
,
,负值舍去,
;
如图,在上截取,连接,
,,
,
,,,
≌,
,,
,
,,
,,
,
,
,
,
,
,
正方形与的面积之比:.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.化简的结果是( )
A. B. C. D.
2.下列计算正确的是( )
A. B. C. D.
3.在中,,,,则的长为( )
A. B. C. D.
4.由下列各组线段围成的三角形中,是直角三角形的是( )
A. ,, B. ,, C. ,, D. ,,
5.甲、乙、丙、丁四名同学进行分钟跳绳测试,每人次分钟跳绳成绩的平均数都是个,方差分别是,,,,则这四名同学分钟跳绳成绩最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
6.将一元二次方程化为一元二次方程的一般形式,其中二次项系数为,一次项系数和常数项分别是( )
A. , B. , C. , D. ,
7.关于的一元二次方程有两个不相等的实数根,则的取值范围是( )
A. B. C. 且 D. 且
8.如图,在菱形中,,对角线,则菱形的面积是( )
A.
B.
C.
D.
9.下列有关一次函数的说法中,正确的是( )
A. 的值随着值的增大而增大 B. 函数图象与轴的交点坐标为
C. 当时, D. 函数图象经过第二、三、四象限
10.在平面直角坐标系中,点坐标为,点坐标为,则,之间距离的最小值为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.二次根式有意义,则的取值范围是______.
12.一组数据为,,,,则这组数据的方差是______.
13.如图,周长为菱形的对角线相交于点,为的中点,
连接则的长为______.
14.方程的两个实数根分别是,,则的值是______.
15.函数的图象如图所示,则关于的不等式的解集是______.
16.如图,平行四边形中,,,,,分别是边,上的动点,且,则的最小值为______.
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:.
18.本小题分
解下列方程:
;
.
19.本小题分
如图,在矩形中,,分别是,上的点,连接,,若,求证:.
20.本小题分
某校为了解学生在学校甲、乙超市的生活消费情况,各随机抽查了名学生某一周按周一至周五算的消费金额单位:元,并将数据进行收集、整理和分析下面给出了部分信息.
消费金额的频数分布表如下:
消费金额元
甲超市
乙超市
乙超市消费金额在这一组的是:
甲、乙两个超市消费金额的平均数、中位数、众数如表:
超市 平均数 中位数 众数
甲
乙
根据以上信息,回答下列问题:
求表中和的值;
若甲超市该周的学生消费人数为人,估计甲超市一个月按周算的学生消费总金额.
21.本小题分
已知:如图,在矩形中,是边上的点,连接.
尺规作图,以为边,为顶点作,交线段于点要求:基本作图,保留作图痕迹,不写作法,不下结论.
求证:四边形为平行四边形
22.本小题分
某商店计划采购甲、乙两种不同型号的电视机进行销售.知商店购进甲型电视机台,乙型电视机台,需要花费元.进甲型电视机台,乙型电视机台,需要花费元.
求该商店购进甲、乙两种型号的电视机的单价分别为多少元?
该商店购进甲、乙两种型号的电视机共台,且购买的甲型电视机的数量不多于乙型电视机数量的倍.甲型电视机的售价为元台,乙型电视机的售价为元台,全部卖出,问:应购进甲种型号的电视机多少台?才能使该商店销售甲、乙两种不同型号的电视机获得的总利润最大,最大总利润是多少?
23.本小题分
综合实践:阅读下列材料,解答问题.
任务:如图,一块锐角三角形木料,现要测量边上的高.
工具:如图,一把刻度尺宽度为,两端受损,可测量长度大于的各边长.
小明的测量过程如下:
步骤一:如图,测得;
步骤二:在边上测得;
步骤三:测得点在边上;
步骤四:测得.
小颖的测量过程如下:
步骤一:如图,将刻度尺的一边与边重叠,另一边与边交点为,与的交点为;
步骤二:测得;测得.
小明的测量方法是通过测量操作得到,由此判定就是边上的高用你所学的知识说明小明如何判定是边上的高.
请根据小颖的测量方法和所得到的数据,求出边上的高结果用含字母,,的式子表示.
24.本小题分
在平面直角坐标系中,一次函数与为常数,且的图象相交于点.
当时,求点的坐标;
与的关系式记作函数,函数满足:当时,;当时,.
若函数的图象与轴总有两个不同的交点,求的取值范围;
在的条件下,当时,的最大值与最小值的差为,求的值.
25.本小题分
如图,在正方形中,点在边上不与点,重合,交对角线于点,交于点.
求证:.
若,,求的长.
如图,连接,,若,求正方形与的面积之比.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:原式
.
18.解:;
;
开方得:,
解得:,;
分解因式得:,
解得:,.
19.证明:四边形是矩形,
,,
在和中,
,
≌,
.
20.解:元,
第和第个数据为和,
元,
即表中的值为,的值为;
元,
答:估计甲超市一个月按周算的学生消费总金额为元.
21.解:如图所示,即为所求;
证明:四边形为矩形,
,,,,
,
在和中,
,
≌,
,
,
即,
四边形为平行四边形.
22.解:设商店购进甲种型号的电视机的单价为元,购进乙种型号的电视机的单价为元,
根据题意得:,
解得,
答:商店购进甲种型号的电视机的单价为元,购进乙种型号的电视机的单价为元;
设获得的总利润为元,购进甲种型号的电视机台,
购买的甲型电视机的数量不多于乙型电视机数量的倍,
,
解得,
根据题意得,
,
随的增大而增大,
时,取最大值,最大值为元,
答:购进甲种型号的电视机台,才能使该商店销售甲、乙两种不同型号的电视机获得的总利润最大,最大总利润是元.
23.证明:连接,以为圆心,长为半径作圆,
,
、在圆上,且是直径,
,即是边上的高;
判定是边上的高用到的几何知识是:直径所对的圆周角是直角;
解:过点作交于点,交于点,则,,设,则,
,即,
,
,
边上的高为.
24.解:当时,一次函数与为与,
,解得,
点的坐标为;
根据题意,得
,
解得,
点坐标为,
函数的图象与轴总有两个不同的交点,
;
由得,交点的横坐标为,即,
,,
由图象可知,当时,即当,且时,即,
时,,
时,,
时,,
,
时,,
当时,的最大值与最小值的差为,
,
解得符合题意,
当时,即,
时,函数的解析式为,
,
随着的增大而减小,
时,,
时,,
当时,的最大值与最小值的差为,
,
解得不合题意,舍去,
综上所述,的值为.
25.证明:连接,
四边形是正方形,
,,,
又,
≌,
,,
,且,
,
,
,
,
,
;
如图,过点作于,
,,
,
,
,,
,,
,
,
,负值舍去,
;
如图,在上截取,连接,
,,
,
,,,
≌,
,,
,
,,
,,
,
,
,
,
,
,
正方形与的面积之比:.
第1页,共1页
同课章节目录
