三角形的外角

课件25张PPT。 你和别人的差距
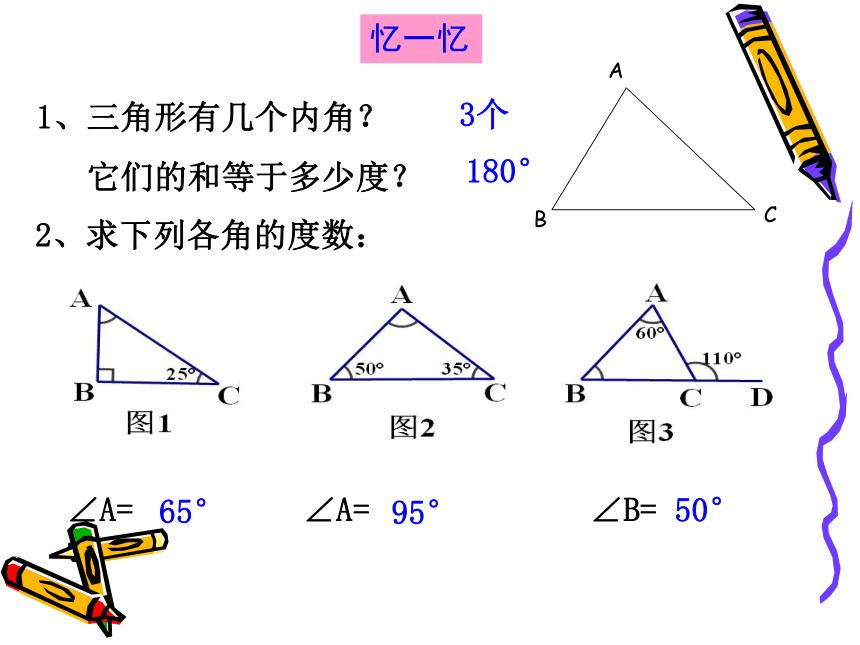
知道是什么吗？就是看你会不会思考，能不能抓住你身边的每一分每一秒的空闲时间！2、求下列各角的度数：1、三角形有几个内角？
它们的和等于多少度？65°3个180°95°∠A= ∠A= ∠B=50°忆一忆三角形的外角学习目标:
1、理解三角形的外角概念，掌握三角形外角的2条 性质。
2 、进一步学会用几何符号语言推理、计算三角形相关的角，初步接触到不等关系的证明．
重点:
三角形的外角及其性质．
难点:
运用三角形外角性质进行有关计算证明，能准确地表达推理的过程和方法．
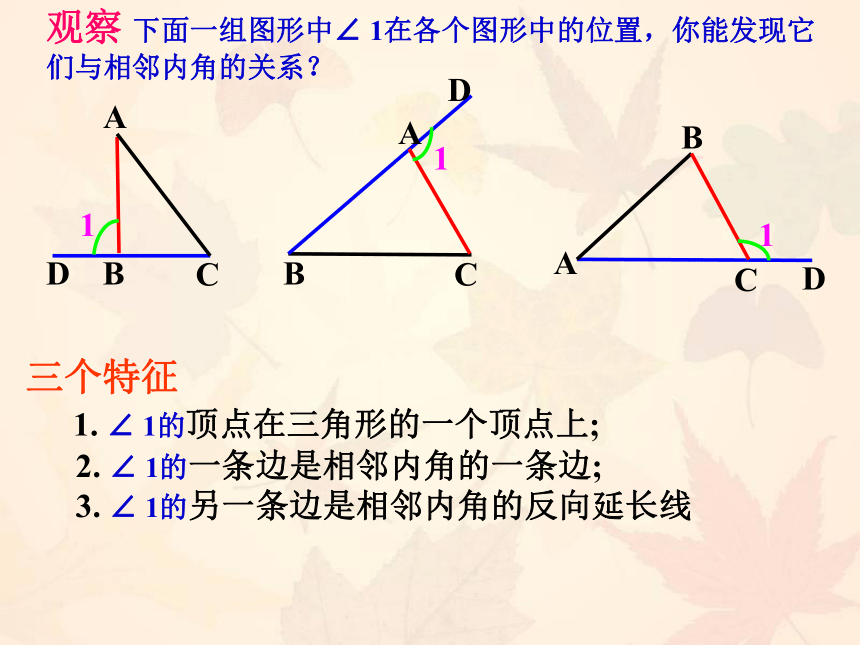
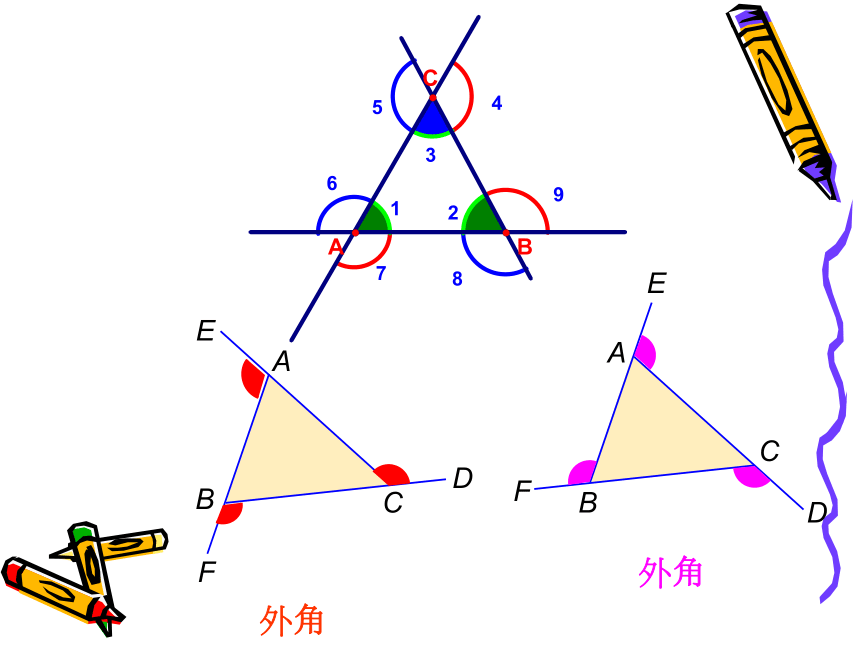
观察 下面一组图形中∠ 1在各个图形中的位置，你能发现它们与相邻内角的关系？
三个特征
1. ∠ 1的顶点在三角形的一个顶点上;
2. ∠ 1的一条边是相邻内角的一条边;
3. ∠ 1的另一条边是相邻内角的反向延长线
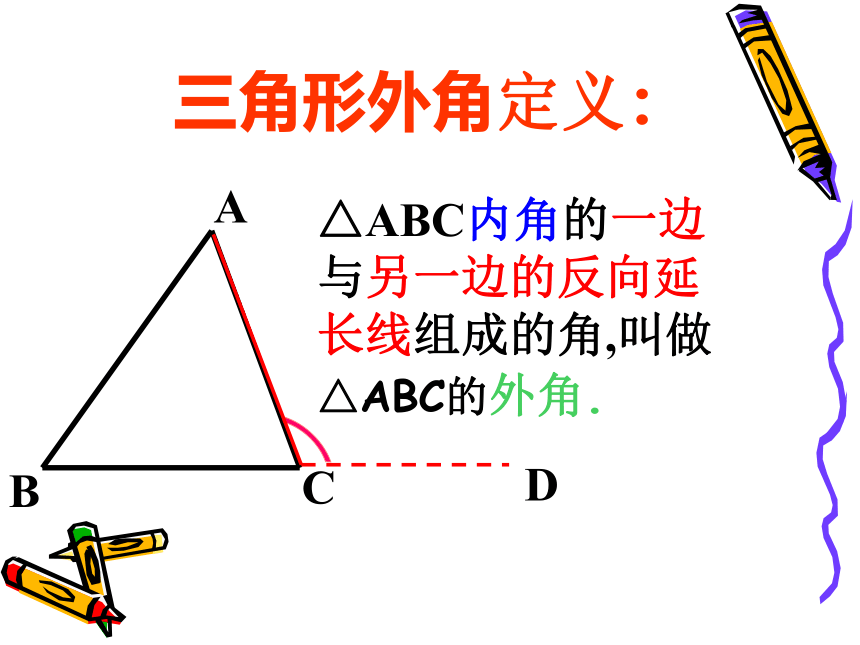
D三角形外角定义：△ABC内角的一边与另一边的反向延长线组成的角,叫做△ABC的外角.大家一起画一画 想一想:
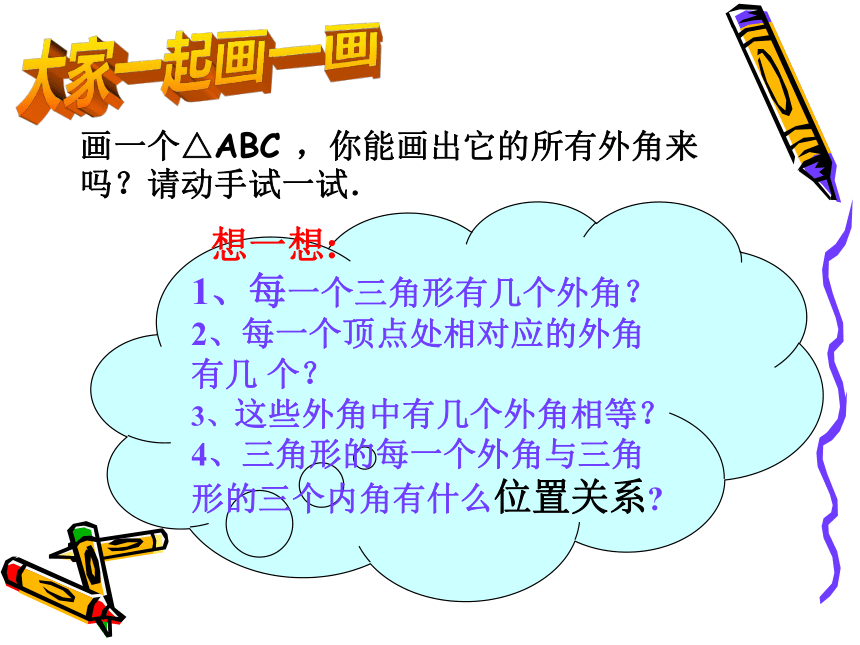
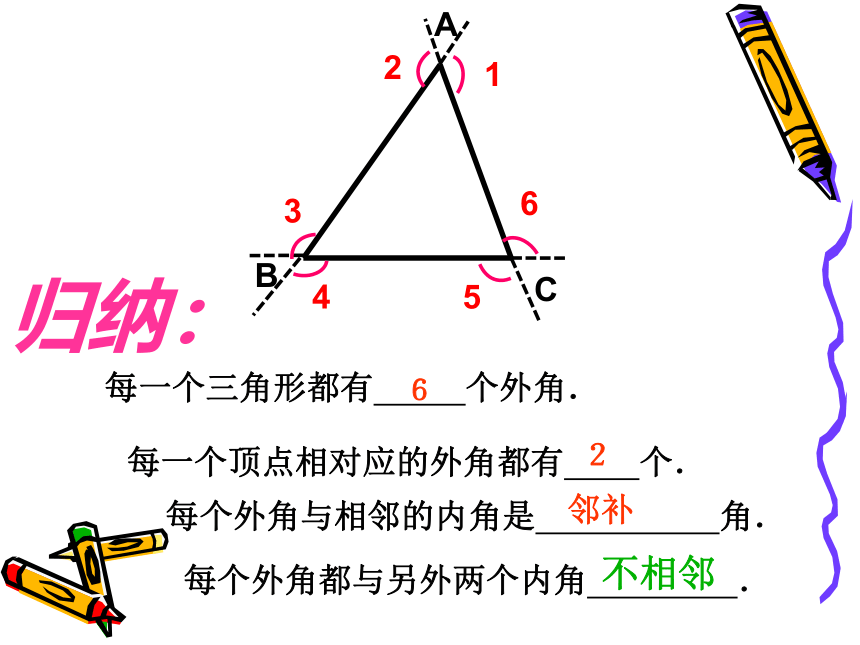
1、每一个三角形有几个外角？
2、每一个顶点处相对应的外角有几 个？
3、这些外角中有几个外角相等？4、三角形的每一个外角与三角形的三个内角有什么位置关系?
画一个△ABC ，你能画出它的所有外角来吗？请动手试一试．　归纳： ABC123465　　每一个三角形都有 个外角．
每一个顶点相对应的外角都有 个． 每个外角与相邻的内角是 角．６２邻补 每个外角都与另外两个内角 ．不相邻趁热打铁:
你能在下图中填出已知角是哪个三角形的外角或内角吗？ 1.∠ BEF是（ ）的外角，也是（
）的内角。2.∠ BDC是（ ）的外角，也是（
）的内角。 3.∠ BFC是（ ）的外角，
也是（ ） 的内角。 内外角是相对而言的.内外角是相对而言的.内外角是相对而言的△AEC△BEF、△BEC△ABD△BDC 、 △CDF △BEF、 △ CDF△BFC ABCDE看一看：算一算：探究？图中哪些角是三角形的内角，
哪些角是三角形的外角？
⌒⌒⌒⌒⌒115°60°65°55°125°　通过上题的计算，你发现∠ACD， ∠ CAE与三角形的内角之间有怎样的数量关系呢？请你试着用自己的语言说一说．想一想：三角形的一个外角等于
与它不相邻的两个内角的和。ACDE⌒⌒⌒⌒⌒115°60°65°55°125°外角性质定理1：证明：在△ABC中，∠A+∠B+∠ACB=180°
又因为∠ACD+∠ACB=180°
所以∠ACD=∠A+∠B尝试用严格的用几何符号语言证明这个结论？已知：∠ACD是△ABC的一个外角求证：∠ACD=∠A+∠B定理1：三角形的一个外角等于与它不 相邻的两个内角的和。三种语言表述求下列各图中∠1的度数。∠1=∠1=∠1=90o85o95o熟练运用 ∠ACD ∠A (<、>)；∠ACD ∠B (<、>)三角形的一个外角大于任何一个与它不相邻
的内角。
D>>你选什么 ？外角性质定理2：定理2揭示的结论与定理1揭示的结论有什么区别和联系？议一议：3、三角形的一个外角 任何一个与 它 的内角。2、三角形的一个外角等于与它 的两个内角的 ；1、三角形的一个外角与它相邻的内角互为 ；三角形的外角与内角的关系：邻补角不相邻大于不相邻和及时总结：如图，比较图中∠1、 ∠2、 ∠3大小，并按大小排序，说明理由。∴∠1∠2∠3＞＞∵∠BEC是△BDE的外角∠2∵∠2是△ACD的外角证明：∴∠1＞∠2 ＞∠3比一比：看谁能用规范的
符号语言证明？自主探究1．三角形的一个外角等于两个内角和．（　　）
2．三角形的一个外角等于与它不相邻的两个内角的和．（　　）
3．三角形的一个外角大于任何一个内角．（　　）
4．三角形的一个内角小于任何一个与它不相邻的外角． （　　） 下列说法正确吗？√×√×辨一辨5. 三角形的一个外角小于与它相邻的内角，则这个三角形是锐角三角形（ ）×6. 三角形的一个外角等于于与它相邻的内角，
则这个三角形是直角三角形（ ）√合作探究由此题你能得到
三角形的三个外角和是 360°解法一：
∵　∠1 =∠ABC +∠ACB，
∠2 =∠BAC +∠ACB，
∠3 =∠BAC +∠ABC，
∴　∠1 +∠2 +∠3=
（∠ABC+∠ACB）+（∠BAC +∠ACB）+ （∠BAC +∠ABC）= 2（∠ABC +∠BAC +∠ACB）．
∵　∠ABC +∠BAC+∠ACB =180°，
∴　∠1 +∠2 +∠3
= 2×180°=360°.∠2＋ ∠ABC=180°∠3＋ ∠ACB=180°三个式子相加得到∠1＋ ∠2＋ ∠3＋ ∠BAC＋ ∠ABC＋∠ACB=540°而∠BAC＋ ∠ABC＋∠ACB=180°∠1＋ ∠2＋ ∠3＝360°做一做如图，D是△ABC的BC边上
一点，∠B＝∠BAD，∠ADC=80°,∠BAC=70°.
求：（1）∠B的度数；（2）∠C的度数.问：（1）中为什么∠ADC＝∠B+∠BAD？
（2）中求∠C的度数还有其他方法吗？ 【练习】如图， CE是△ABC 的外角∠ACD 的平分线，且CE 交BA 的延长线于点E ，
证明：∠BAC>∠B ．
拓展延伸，灵活运用 1、直接不好证明找中间角过渡
2、，同一个角，在不同的三角形中可能是外角或者内角启示 小结1、三角形外角的两条性质① 三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
再 见 你和别人的差距知道是什么吗？就是看你会不会思考，能不能抓住你身边的每一分每一秒的空闲时间！