人教版数学八年级上册 课件:13.3《等腰三角形的判定》(共12张PPT)
文档属性
| 名称 | 人教版数学八年级上册 课件:13.3《等腰三角形的判定》(共12张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 36.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-24 14:43:52 | ||
图片预览



文档简介
课件12张PPT。等腰三角形的判定学习目标:会推证等腰三角形的判定定理及其推论,并会阐述等腰三角形的判定定理及其推论;
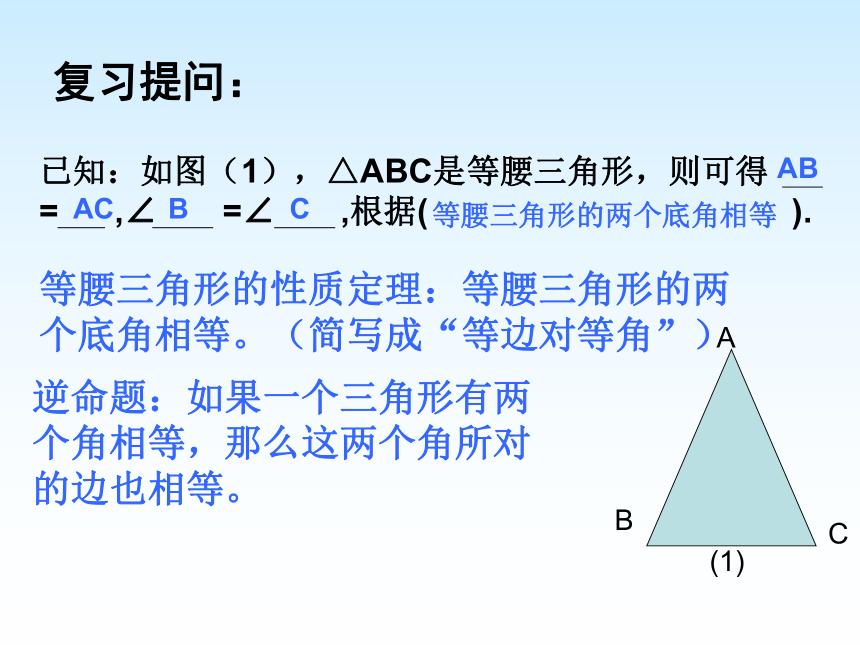
会运用等腰三角形的判定定理证明一个三角形是等腰三角形;会综合应用等腰三角形性质定理和判定定理。已知:如图(1),△ABC是等腰三角形,则可得 = ,∠ =∠ ,根据( ).复习提问:AB CA(1)ABACBC等腰三角形的两个底角相等等腰三角形的性质定理:等腰三角形的两个底角相等。(简写成“等边对等角”)逆命题:如果一个三角形有两个角相等,那么这两个角所对的边也相等。例题解析:等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等。
(简写成“等角对等边”)已知:△ABC中,∠B=∠C,如图求证:AB=AC。证明:作∠BAC的平分线AD,则∠1 = ∠2
在△BAD和△CAD中,∴△BAD≌△CAD(AAS)∴AB=AC(全等三角形对应边相等)D21∠B=∠C
∠1 = ∠2
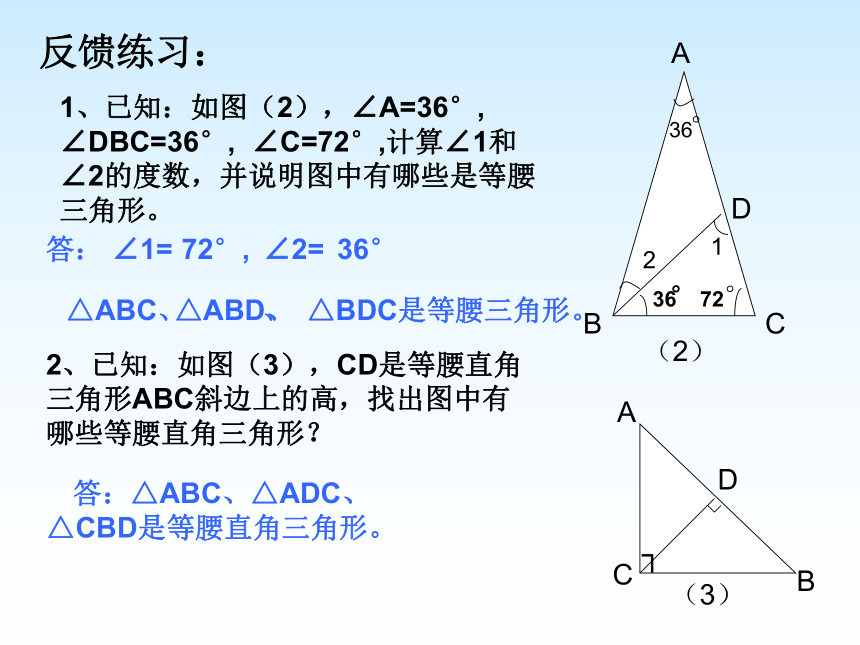
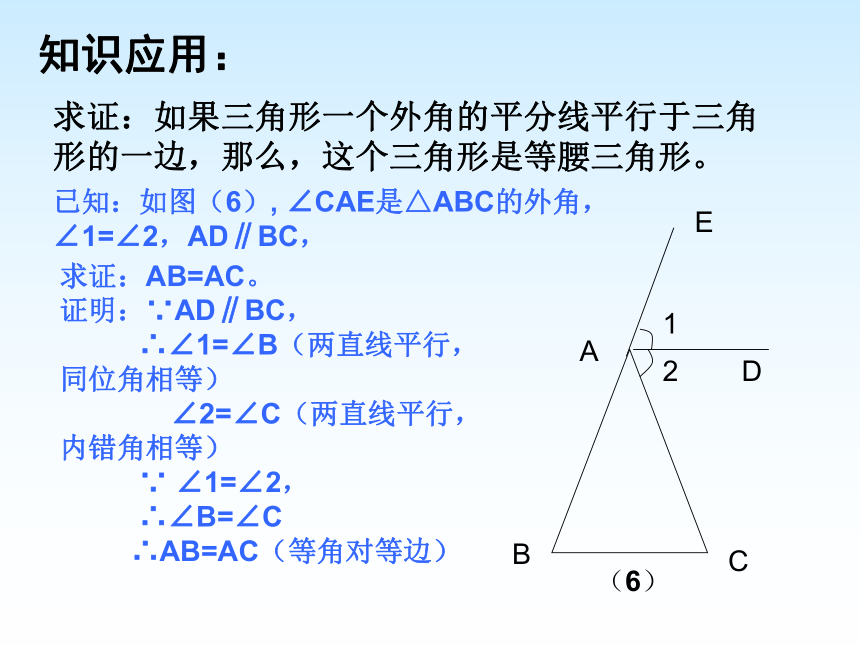
AD=AD (公共边) 反馈练习:1、已知:如图(2),∠A=36°, ∠DBC=36°, ∠C=72°,计算∠1和∠2的度数,并说明图中有哪些是等腰三角形。2、已知:如图(3),CD是等腰直角三角形ABC斜边上的高,找出图中有哪些等腰直角三角形?ABCD36°1236°°7236°是等腰三角形。(2)ACBD┐(3)答:△ABC、△ADC、 △CBD是等腰直角三角形。求证:如果三角形一个外角的平分线平行于三角形的一边,那么,这个三角形是等腰三角形。已知:如图(6), ∠CAE是△ABC的外角,∠1=∠2,AD∥BC,求证:AB=AC。证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等)
∠2=∠C(两直线平行,内错角相等)
∵ ∠1=∠2,
∴∠B=∠C
∴AB=AC(等角对等边)知识应用:(6)12D巩固练习:1、根据下列条件指出各个图形中哪个三角形是等腰三角形?(1)如图(7),BD平分∠ABC,DE∥AB;(2)如图(8),AD平分∠BAC,CE∥AD;(7)答: △BED是等腰三角形3(8)证明:∵AD平分∠BAC
∴∠1=∠2 ∵AD∥EC
∴∠1=∠E, ∠2=∠3 ∴∠3=∠E ∴△ACE是等腰三角形212、已知:如图(9),AD∥BC,BD平分∠ABC,
求证:AB=AD。ABCD312(9)证明:∵BD平分∠ABC
∴∠1=∠2
∵AD∥BC
∴∠2=∠3
∴∠1=∠3
∴AB=AD(等角对等边)4、已知:如图(11),AB=AD,∠ADC=∠ABC,
求证:CB=CD。证明:连接BD
∵AB=AD
∴∠ABD∠ADB(等边对等角)
又∵∠ABC=∠ADC
∴∠ABC-∠ABD=∠ADC-∠ADB
即,∠CBD=∠CDB
∴CB=CD(等角对等边)(11)3、已知:如图(10),∠1=∠2, ∠3=∠4,DE∥BC;
求证:DE=DB+EC。ABDCEF1234(10)证明:
∵DE∥BC
∴∠2=∠DFB,∠3=∠EFC
又∵∠1=∠2,∠3=∠4
∴∠1=∠DFB,∠4=∠EFC
∴DF=BD, EF = EC
又∵DE=DF+EF
∴DE=DB+EC小结:
1、证明三角形是等腰三角形的方法:
(1)等腰三角形的定义;
(2)等腰三角形的判定定理。
2、证明三角形是等边三角形的方法:
(1)等边三角形的定义;
(2)推论1:三个角都相等的三角形是等边三角形;
(3)推论2:有一个角等于60°的等腰三角形是等边三角形。
再见!
会运用等腰三角形的判定定理证明一个三角形是等腰三角形;会综合应用等腰三角形性质定理和判定定理。已知:如图(1),△ABC是等腰三角形,则可得 = ,∠ =∠ ,根据( ).复习提问:AB CA(1)ABACBC等腰三角形的两个底角相等等腰三角形的性质定理:等腰三角形的两个底角相等。(简写成“等边对等角”)逆命题:如果一个三角形有两个角相等,那么这两个角所对的边也相等。例题解析:等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等。
(简写成“等角对等边”)已知:△ABC中,∠B=∠C,如图求证:AB=AC。证明:作∠BAC的平分线AD,则∠1 = ∠2
在△BAD和△CAD中,∴△BAD≌△CAD(AAS)∴AB=AC(全等三角形对应边相等)D21∠B=∠C
∠1 = ∠2
AD=AD (公共边) 反馈练习:1、已知:如图(2),∠A=36°, ∠DBC=36°, ∠C=72°,计算∠1和∠2的度数,并说明图中有哪些是等腰三角形。2、已知:如图(3),CD是等腰直角三角形ABC斜边上的高,找出图中有哪些等腰直角三角形?ABCD36°1236°°7236°是等腰三角形。(2)ACBD┐(3)答:△ABC、△ADC、 △CBD是等腰直角三角形。求证:如果三角形一个外角的平分线平行于三角形的一边,那么,这个三角形是等腰三角形。已知:如图(6), ∠CAE是△ABC的外角,∠1=∠2,AD∥BC,求证:AB=AC。证明:∵AD∥BC,
∴∠1=∠B(两直线平行,同位角相等)
∠2=∠C(两直线平行,内错角相等)
∵ ∠1=∠2,
∴∠B=∠C
∴AB=AC(等角对等边)知识应用:(6)12D巩固练习:1、根据下列条件指出各个图形中哪个三角形是等腰三角形?(1)如图(7),BD平分∠ABC,DE∥AB;(2)如图(8),AD平分∠BAC,CE∥AD;(7)答: △BED是等腰三角形3(8)证明:∵AD平分∠BAC
∴∠1=∠2 ∵AD∥EC
∴∠1=∠E, ∠2=∠3 ∴∠3=∠E ∴△ACE是等腰三角形212、已知:如图(9),AD∥BC,BD平分∠ABC,
求证:AB=AD。ABCD312(9)证明:∵BD平分∠ABC
∴∠1=∠2
∵AD∥BC
∴∠2=∠3
∴∠1=∠3
∴AB=AD(等角对等边)4、已知:如图(11),AB=AD,∠ADC=∠ABC,
求证:CB=CD。证明:连接BD
∵AB=AD
∴∠ABD∠ADB(等边对等角)
又∵∠ABC=∠ADC
∴∠ABC-∠ABD=∠ADC-∠ADB
即,∠CBD=∠CDB
∴CB=CD(等角对等边)(11)3、已知:如图(10),∠1=∠2, ∠3=∠4,DE∥BC;
求证:DE=DB+EC。ABDCEF1234(10)证明:
∵DE∥BC
∴∠2=∠DFB,∠3=∠EFC
又∵∠1=∠2,∠3=∠4
∴∠1=∠DFB,∠4=∠EFC
∴DF=BD, EF = EC
又∵DE=DF+EF
∴DE=DB+EC小结:
1、证明三角形是等腰三角形的方法:
(1)等腰三角形的定义;
(2)等腰三角形的判定定理。
2、证明三角形是等边三角形的方法:
(1)等边三角形的定义;
(2)推论1:三个角都相等的三角形是等边三角形;
(3)推论2:有一个角等于60°的等腰三角形是等边三角形。
再见!
